Содержание
- 2. ОПРЕДЕЛИТЕЛИ 1). Определитель второго порядка равен разности произведения элементов, стоящих на главной и побочной диагонали. Определители
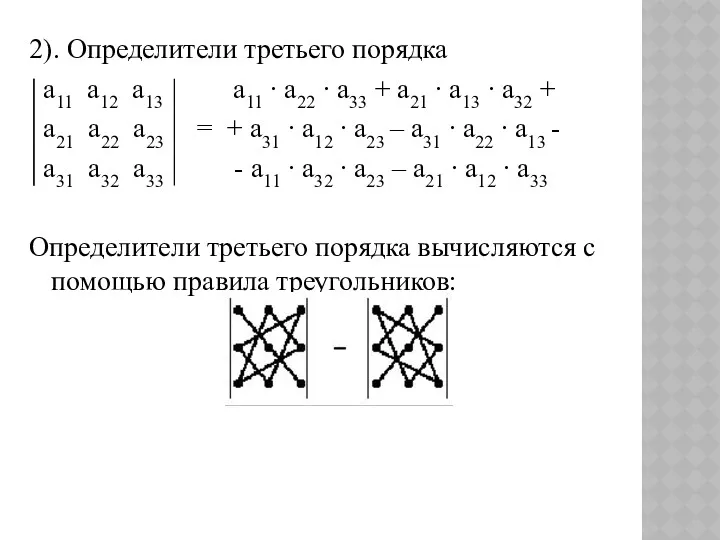
- 3. 2). Определители третьего порядка а11 а12 а13 а11 ∙ а22 ∙ а33 + а21 ∙ а13
- 4. При умножении элементов любого столбца определителя на число α, его величина умножается на это же число.
- 5. Если к одному из столбцов определителя прибавить другой, умноженный на произвольное число, то величина определителя не
- 6. Минором любого элемента определителя называется определитель , полученный вычеркиванием строки и столбца на пересечении которых находится
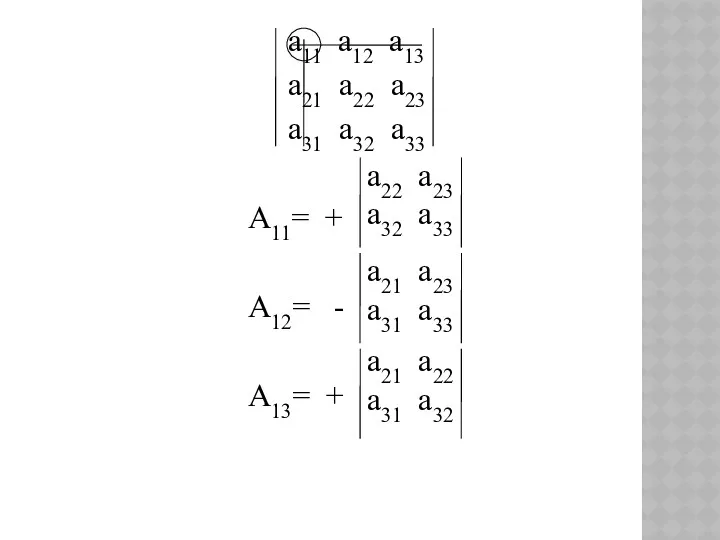
- 7. а11 а12 а13 а21 а22 а23 а31 а32 а33 А11= + А12= - А13= + а22
- 8. Любой определитель можно представить в виде суммы произведений элементов какой-либо строки или столбца на их алгебраические
- 9. РЕШЕНИЕ СИСТЕМ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ a11x1+ a12x2=b1 x1, x2 - неизвестные a21x1+ a22x2=b2
- 10. РЕШЕНИЕ СИСТЕМ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ТРЕМЯ НЕИЗВЕСТНЫМИ a11x1+ a12x2+ a13x3 =b1 x1, x2, x3 -
- 11. Если определитель ∆ не равен 0, то система имеет единственное решение, которое находится по формуле:
- 12. Матрицей называется система элементов, расположенных в определенном порядке и образующих таблицу. А= аij – элементы определителя
- 13. Квадратной матрицей n-го порядка называется матрица размера n×n. Прямоугольной матрицей называется матрица, в которой m≠n. Единичной
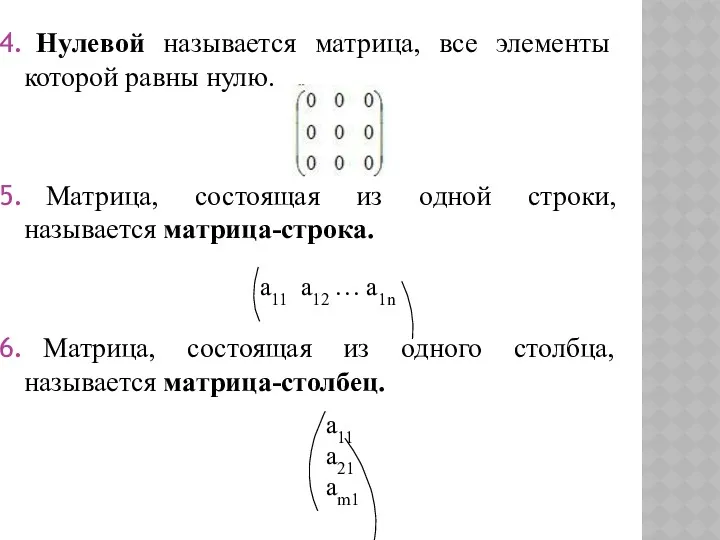
- 14. Нулевой называется матрица, все элементы которой равны нулю. Матрица, состоящая из одной строки, называется матрица-строка. Матрица,
- 15. Транспонированная матрица (АТ) — матрица, полученная из исходной матрицы заменой строк на столбцы. А= АТ= Две
- 16. Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.
- 17. Произведением матрицы Am×n на матрицу Bn×k называется матрица Cm×k такая, что элемент матрицы C, стоящий в
- 19. Скачать презентацию













 Игра Математика в мире животных и животные в мире математики
Игра Математика в мире животных и животные в мире математики Формула Байеса
Формула Байеса Функция y=sinx, ее свойства и график
Функция y=sinx, ее свойства и график Исследование отклика в области эксперимента
Исследование отклика в области эксперимента Открытый урок по математике в 6 классе
Открытый урок по математике в 6 классе Подобные треугольники. Пропорциональные отрезки
Подобные треугольники. Пропорциональные отрезки Задачи на готовых чертежах. Квадрат
Задачи на готовых чертежах. Квадрат Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Общие методы решения уравнений
Общие методы решения уравнений Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам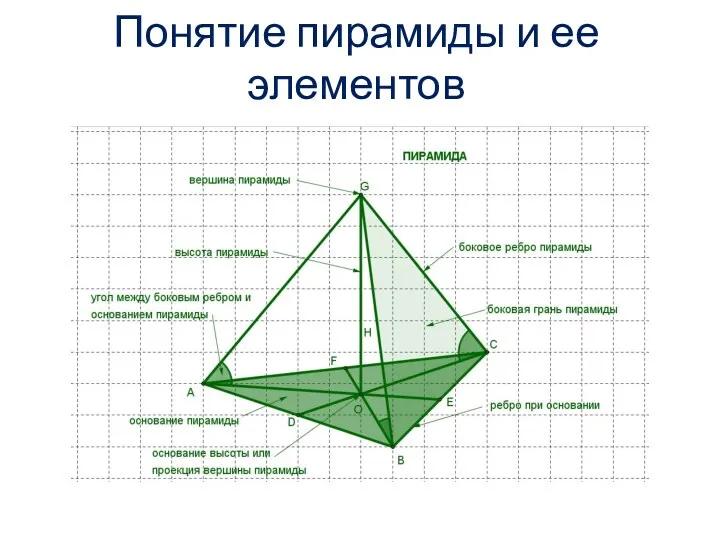 Понятие пирамиды и ее элементов. Правильная пирамида
Понятие пирамиды и ее элементов. Правильная пирамида Теорема Виета
Теорема Виета Урок математики 4 класс Измерение площади фигуры палеткой
Урок математики 4 класс Измерение площади фигуры палеткой Решение задач с помощью уравнений. Алгебра, 7 класс
Решение задач с помощью уравнений. Алгебра, 7 класс Мәтінді есептерді теңдеу. Құрып шығару
Мәтінді есептерді теңдеу. Құрып шығару Занимательная математика Арифметика в гостях у насекомых
Занимательная математика Арифметика в гостях у насекомых Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями
Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр
Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр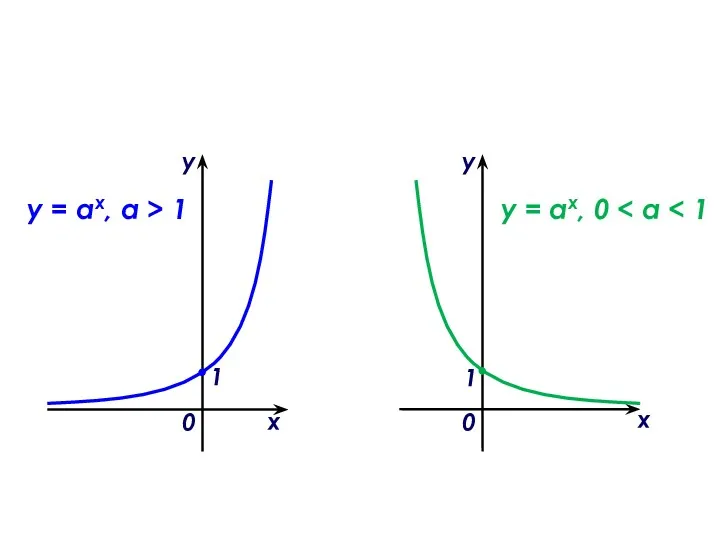 Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Умножение числа 10
Умножение числа 10 Использование ИКТ
Использование ИКТ Квадратные неравенства (8 класс)
Квадратные неравенства (8 класс) Шуточные математические задачи
Шуточные математические задачи Линейная функция и её график
Линейная функция и её график Подготовка к ЕГЭ по математике. Решение заданий В9
Подготовка к ЕГЭ по математике. Решение заданий В9 Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Сравнение чисел по модулю m
Сравнение чисел по модулю m Численные методы решения систем уравнений
Численные методы решения систем уравнений