Содержание
- 2. Применение производной при исследовании функции Теорема о необходимых признаках возрастания и убывания функции. 1. Если функция
- 3. 2. Если функция y=f(x) дифференцируема и убывает на интервале (a,b), то производная этой функции не положительна
- 4. Экстремумами функции называются её точки максимума и минимума. Производная дифференцируемой функции в точке экстремума равна нулю.
- 5. 1. Найти область определения функции, которая может быть конечной или бесконечной. 2.Найти производную функции и определить
- 6. 4. Найти критические точки функции, как совокупность всех стационарных точек и точек в которых производная не
- 7. 7. Найти точки экстремумов функции. Пример. Исследовать функцию 1. Область определения этой функции (-∞,∞) 2.Производная 3.
- 8. 5.Определим знаки производных в интервалах (-∞,0),(0,2),(2,∞).Для этого достаточно найти знак производной в любой точке интервала. На
- 9. Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если
- 10. Неопределенный интеграл. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) +
- 12. Свойства: где u, v, w – некоторые функции от х. Пример:
- 13. Методы интегрирования А) Непосредственное интегрирование.
- 14. Б) Способ подстановки (замены переменных).
- 15. В) Интегрирование по частям.
- 16. Пример. Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному
- 18. Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)
- 19. Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x)
- 20. Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a
- 21. 5.Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b],
- 22. 8. Для произвольных чисел a, b, c справедливо равенство: Теорема: (Теорема Ньютона – Лейбница) Если функция
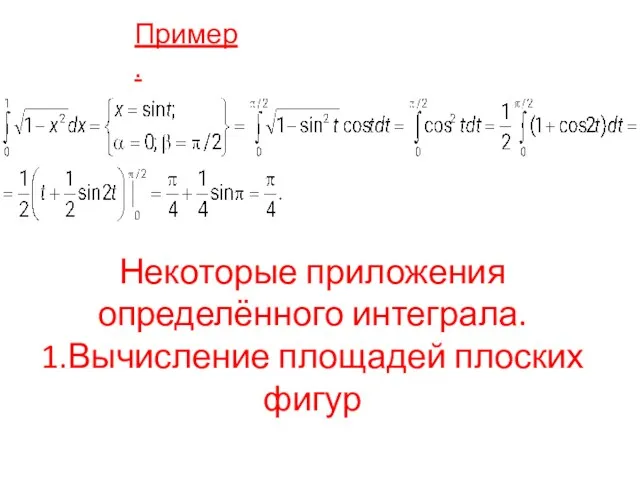
- 23. Пример. Некоторые приложения определённого интеграла. 1.Вычисление площадей плоских фигур
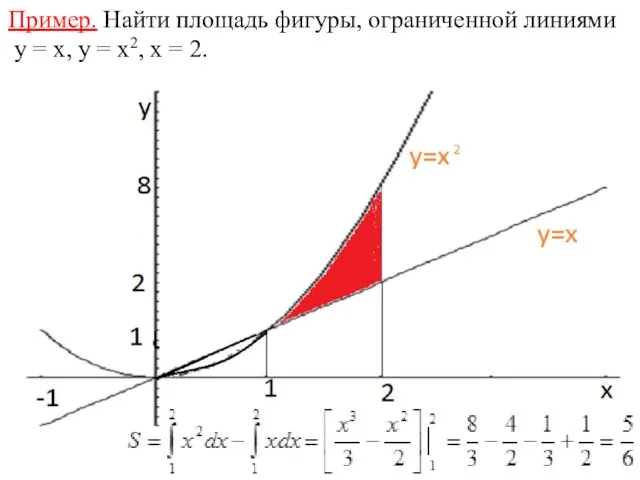
- 24. Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
- 25. 2. Вычисление работы переменной силы. Пример. Найти работу для растяжения пружины от равновесного состояния на величину
- 27. Скачать презентацию















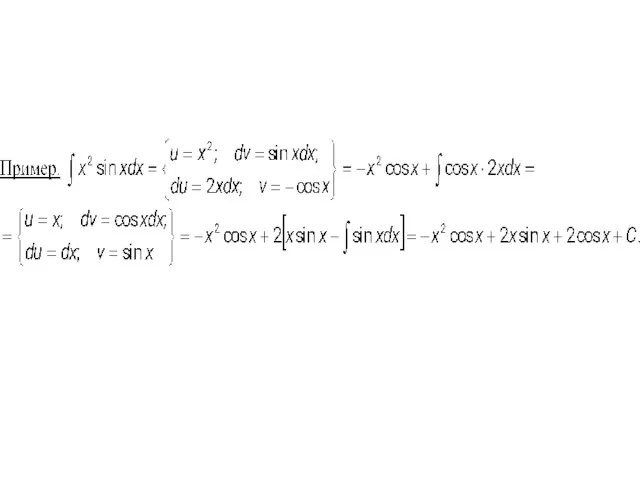
![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/427677/slide-17.jpg)

![Свойства определенного интеграла. 4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/427677/slide-19.jpg)



 Линейная функция и её график
Линейная функция и её график Вневписанная окружность
Вневписанная окружность Отклонения. Частота в массиве. Урок по вероятности и статистике
Отклонения. Частота в массиве. Урок по вероятности и статистике Корень n-й степени. Упражнение 9
Корень n-й степени. Упражнение 9 Геометрия сызымнарда (7 класс)
Геометрия сызымнарда (7 класс) Конспект НОД по ФЭМП По следам Колобка
Конспект НОД по ФЭМП По следам Колобка Пирамида
Пирамида Многочлены
Многочлены Столбчатые диаграммы и графики
Столбчатые диаграммы и графики Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Приёмы письменных вычислений
Приёмы письменных вычислений Координаты вектора
Координаты вектора Статистическая сводка и группировка
Статистическая сводка и группировка Действия с числами
Действия с числами Математический анализ: трендовые индикаторы. Базовый курс
Математический анализ: трендовые индикаторы. Базовый курс Ох,уж эта математика! Команды Квадрат и Звезды
Ох,уж эта математика! Команды Квадрат и Звезды Загадки. Натуральные числа
Загадки. Натуральные числа Презентация к уроку математики во 2 классе УМК ПНШ по теме Увеличение в несколько раз
Презентация к уроку математики во 2 классе УМК ПНШ по теме Увеличение в несколько раз Тренажёр В гости к Матроскину. Математика 1 класс
Тренажёр В гости к Матроскину. Математика 1 класс тренажёр сложение и вычитание трёхзначных чисел
тренажёр сложение и вычитание трёхзначных чисел презентация по математика на тему Сколько?
презентация по математика на тему Сколько? Математика, тест. (3 класс)
Математика, тест. (3 класс) Математика о вреде курения. 6 класс
Математика о вреде курения. 6 класс Математичний пакет Mathematica. Лекція №4
Математичний пакет Mathematica. Лекція №4 Определение. Примеры. Классификация и характеристика методов решения систем линейных уравнений
Определение. Примеры. Классификация и характеристика методов решения систем линейных уравнений Программа курса по высшей математике
Программа курса по высшей математике Задачи на движение
Задачи на движение Сикһеҙ геометрик прогрессия
Сикһеҙ геометрик прогрессия