Определение. Примеры. Классификация и характеристика методов решения систем линейных уравнений презентация

Определение. Примеры.
К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи (уравнения материального баланса, уравнения теплового баланса, численное решение краевых задач для дифференциальных уравнений, моделирование некоторых специальных инженерных задач и др.).
Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики. Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

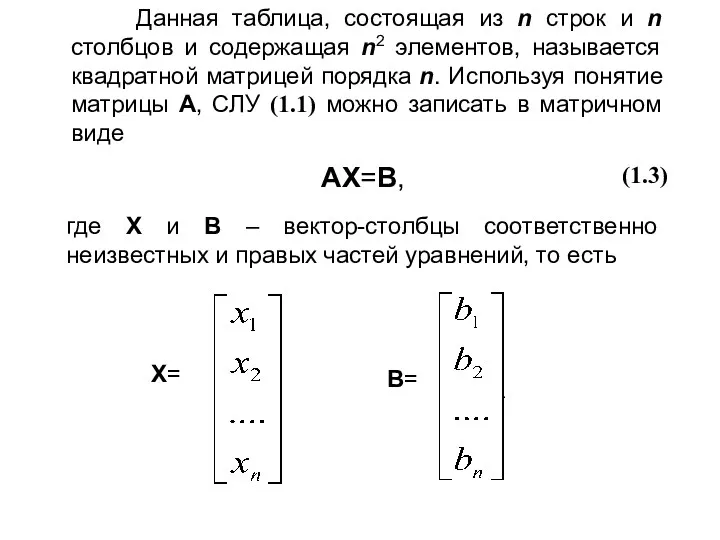
Данная таблица, состоящая из n строк и n столбцов и содержащая n2 элементов, называется квадратной матрицей порядка n. Используя понятие матрицы А, СЛУ (1.1) можно записать в матричном виде
(1.3)
AX=B,
где X и B – вектор-столбцы соответственно неизвестных и правых частей уравнений, то есть
X=
B=
.

Определителем (детерминантом) матрицы А n-го порядка называется число D (иногда обозначают det A), равное
(1.4)
где индексы α, β,..., ω пробегают все возможные n! перестановок номеров 1, 2, ... ,n; k – число инверсий в данной перестановке.
Необходимым и достаточным условием существования единственного решения СЛУ является условие D≠0.
В случае D=0 матрица называется вырожденной, при этом СЛУ (1.1) либо не имеет решения, либо имеет их бесчисленное множество.
ПРИМЕЧАНИЕ. Матрица A−1 называется обратной по отношению к квадратной матрице A, если их произведение равно единичной матрице: AA−1 = A−1 A= E. Всякая невырожденная матрица A (т.е. с отличным от нуля определителем) имеет обратную. При этом Det A−1=1/D.
.

2. Классификация и характеристика методов решения систем линейных уравнений
Методы решения СЛУ делятся на две группы:
прямые методы: (изучены в курсе высшей математики)
метод Гаусса;
метод Гаусса-Жордана;
метод Крамера;
матричный метод.
итерационные методы:
метод простой итерации (метод Якоби);
метод Гаусса-Зейделя;
метод прогонки.

Прямые методы решения СЛУ
Прямые методы используют конечные соотношения (формулы) для вычисления неизвестных. Они дают решения после выполнения заранее известного числа итераций. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса линейных систем
Недостатки прямых методов:
требуют хранения в ОЗУ сразу всей матрицы А (при больших n расходуется много места в памяти);
не учитывают структуру матрицы А;
накапливают погрешности в процессе решения, т.к. вычисления на любом этапе используют результаты предыдущих операций (это особенно опасно для систем большой размерности, так как возрастает общее число операций, а так же для плохо обусловленных систем, очень чувствительных к погрешностям, в силу того, что в них детерминант близок к нулю D≈0).

Поэтому прямые методы используют обычно для сравнительно не больших (n<200) СЛУ с плотной матрицей и не близким к нулю детерминантом.
Прямые методы решения иногда называют точными, т.к. решение выражается в виде точных формул через коэффициенты СЛУ. Однако не нужно забывать, что точное решение может быть получено лишь при точных значениях коэффициентов системы, а так же при выполнении вычислений с бесконечным числом разрядов. На практике же, при использовании ЭВМ, вычисления проводятся с ограниченным числом знаков, определяемых разрядностью машины, поэтому неизбежны погрешности в окончательных результатах.

2) Итерационные методы решения СЛУ
Итерационными методами являются методы последовательных приближений. В них, как всегда, нужно задать некоторое приближенное решение – начальное приближение. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с требуемой точностью.
Алгоритмы итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений в них заранее определить трудно. Тем не менее, итерационные методы в ряде случаев предпочтительнее.

Достоинства итерационных методов:
требуют хранения в памяти ЭВМ не всей матрицы системы, а лишь нескольких векторов с n компонентами;
погрешности окончательных результатов не накаплива-ются, т.к. точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполнен-ных вычислений.
В силу указанных достоинств, итерационные методы особенно полезны в случае большого числа уравнений, а так же плохо обусловленных систем. При этом следует отметить, что сходимость итераций может быть очень медленной. В связи с этим, ищутся эффективные пути ее ускорения.
Итерационные методы полезно использовать для уточ-нения решений полученных с помощью прямых методов. Такие смешанные алгоритмы обычно довольно эффективны, особенно для плохо обусловленных систем.

3.3. Итерационные методы
1) Метод уточнения решения
Решения, полученные с помощью прямых методов, обычно содержат погрешности, вызванные округлением при выполнении операций на ЭВМ с ограниченным числом разрядов. Рассмотрим один из методов уточнения решения, найденного прямым методом.
Пусть с помощью некоторого прямого метода вычислены приближенные значения Подставляя их в левые части исходной системы (1.1), получим некоторые значения правой части СЛУ отличные от bi (i=1,2,...,n):

Такой процесс уточнения решения представляет фактически итерационный метод решения СЛУ. При этом для нахождения очередного приближения (на каждой итерации) решаются СЛУ вида (3.5) с одной и той же матрицей, являющейся матрицей исходной системы уравнений, при разных правых частях. В результате каждой итерации получаются новые значения неизвестных.
При малом (с заданной погрешностью E) изменении этих значений на 2-х последовательных итерациях процесс прекращается и происходит вывод значений неизвестных, полученных на последней итерации. Для предотвращения непроизводительных затрат компьютерного времени в случае отсутствия сходимости в алгоритм вводят счётчик числа итераций, при достижении некоторого числа которых счёт прекращается.

2) Метод Гаусса – Зейделя
Один из самых простых и распространенных итерационных методов, легко программируемых.
Рассмотрим метод на примере СЛУ 3-го порядка:
Положим, что диагональные элементы aii (i=1,2,3) отличны от нуля (иначе можно переставить уравнения). Выразим неизвестные x1, x2, x3 соответственно из первого, второго и третьего уравнений системы (3.7):
(3.7)
Зададим некоторые начальные (нулевые) приближения значений неизвестных:
(3.8)

Критерий окончания итерационного процесса:
где E – заданная допустимая погрешность.
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов, т. е.
При этом хотя бы для одного уравнения неравенство должно выполняться строго.

МЕТОД ПРОГОНКИ
Если матрица системы является разреженной (ленточной в рассматриваемом ниже примере), то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки.
Рассмотрим систему уравнений с трех диагональной матрицей.

Для решения данной системы по формулам прямого и обратного хода (прогонки), с использование программного пакета, необходимо ввести обозначения. Обозначим матрицы коэффициентов при неизвестных (диагонально)
Рассмотрим решение системы. Дана система линейных алгебраических уравнений (СЛАУ). Приведём её к виду, удобному для реализации в прикладном пакете

. СР № 4. Прямые методы решения СЛАУ: метод Крамера, матричный метод, метод Гаусса
Задание.
1. Составить систему трёх уравнений с тремя неизвестными.
2. решить заданную систему тремя способами: метод Крамера, метод Гаусса, матричный метод
3. Оформить все методы решения в тетради (примеры см. ниже)

3. Методы решения систем линейных уравнений
3.1. Метод с использованием обратной матрицы
В этом случае система записывается в матричном виде AX=B. Тогда, умножая обе части этого векторного уравнения слева на обратную матрицу A−1, получим X= A−1B. Для вычисления обратной матрицы A−1 могут быть использованы разные методы, например: метод алгебраических дополнений (через алгебраические дополнения и определитель матрицы A); метод Гаусса-Жордано; метод квадратных корней (для симметричной матрицы A) и др. методы.
Метод непригоден для решения СЛУ при больших значениях n, если не использовать экономичных схем для вычисления матрицы A−1 , из-за большого объема вычислений.
, получим

3.2. Метод исключения Гаусса и его модификации
Наиболее распространенным среди прямых методов является метод исключения Гаусса и его модификации. Метод основан на приведении матрицы системы к треугольному виду, что достигается путем последовательного исключения неизвестных из уравнений системы.
Процесс решения СЛУ состоит из прямого хода метода Гаусса и обратного хода метода Гаусса.
1) Алгоритм прямого хода метода Гаусса:
− с помощью первого уравнения исключается переменная x1 из всех последующих уравнений системы;
− затем с помощью второго уравнения исключается x2 из третьего и всех последующих уравнений;
− этот процесс продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным xn, т.е. матрица системы будет приведена к треугольному виду. К такому виду можно привести лишь невырожденную матрицу (иначе метод неприменим).
2) Алгоритм обратного хода метода Гаусса:
− решая последнее уравнение, находим единственное неизвестное xn;
− используя xn, найденное из предыдущего уравнения, находим xn−1 и т.д.;
− последним находится x1 из первого уравнения.

3. Пример решения СЛУ
(i, j=2,3);
(3.1)
Прямой ход. Для исключения x1 из второго уравнения прибавим к нему первое, умноженное на – a21/a11. Аналогично, умножив первое на – a31/a11 и прибавив к третьему, так же исключим x1 из третьего уравнения.
Получим равносильную СЛУ вида
(3.2)
где
(i=2,3).
Рассмотрим применение метода Гаусса для системы третьего порядка:

(3.3)
где
Матрица системы (3.3) имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса. Необходимо заметить, что в процессе исключения неизвестных приходится выполнять операции деления на диагональные коэффициенты и т.д. Поэтому они должны быть отличны от «0». Иначе необходимо соответствующим образом переставить уравнения системы.
Обратный ход. Обратный ход начинается с решения третьего уравнения: x3=b3''/a33''. Используя полученное значение x3, можно найти х2 из второго уравнения, а затем х1 из первого.
Аналогично строится вычислительный алгоритм для линейной системы с произвольным числом n уравнений.
Теперь из третьего уравнения системы (3.2) нужно исключить x2. Для этого умножим второе уравнение на −a32'/a22' и прибавим результат к третьему. Имеем:

4) Метод Гаусса с выбором главного элемента
Одной из модификаций метода Гаусса является схема с выбором главного элемента. Она состоит в том, что требование неравенства нулю диагональных элементов аkk, на которые происходит деление в процессе исключения, заменяется более жестким: из всех оставшихся в k-м столбце элементов нужно выбрать наибольший по модулю элемент, и переставить уравнения так, чтобы этот элемент оказался на месте аkk.
Диагональные элементы называются ведущими элементами: ведущий элемент аkk − это коэффициент при k-м неизвестном в k-м уравнении на k-м шаге исключения. Благодаря выбору наибольшего по модулю ведущего элемента, уменьшаются множители, используемые для преобразования уравнений.
Метод Гаусса с выбором главного элемента обеспечивает приемлемую точность решения для сравнительно не большого числа (n≤100) уравнений. Для плохо обусловленных систем решения полученные по этому методу не надежны. Его целесообразно использовать для решения СЛУ с плотно заполненной матрицей. Все элементы матрицы и правые части СУ находятся в ОЗУ.

Решите систему методом Крамера:
Решение:
Вычислим определитель системы:
Так как определитель системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители :

Решите систему методом Крамера:
Находим неизвестные по формулам Крамера:
Ответ:

Решите систему методом Гаусса:
Решение:
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение умножим на , а затем сложим с 1-ым уравнением.
Аналогично третье уравнение умножим на , а затем сложим с первым.
В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение умножим на , и сложим со вторым. Тогда будем иметь систему уравнений:

Решите систему методом Гаусса:
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем:
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса:
Ответ:

Решите систему матричным методом:
Решение:
Перепишем систему уравнений в матричной форме:
Так как
то систему трёх линейных уравнений с тремя неизвестными можно решить матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как:
⬄
⬄

Решите систему матричным методом:
Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы :
где

Решите систему матричным методом:
Осталось вычислить матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов:
Ответ: .

Пример решения СЛАУ методом Крамера
Ответ: (1; 2; 2; 0)

Пример решения СЛАУ методом Гаусса
Ответ: (1; 2; 2; 0)