Содержание
- 2. Векторы. Линейные операции над векторами. Вектор – направленный отрезок. Обозначение . Длина вектора – длина отрезка
- 3. Векторы. Линейные операции над векторами. 3 Равные векторы – векторы, удовлетворяющие условиям : 1) имеют одинаковую
- 4. Векторы. Линейные операции над векторами. Линейными операциями над векторами называются операции сложения векторов и умножения вектора
- 5. Векторы. Линейные операции над векторами. Произведением вектора ā на число λ называется вектор , удовлетворяющий следующим
- 6. Базис на плоскости и в пространстве. Координаты вектора 6 Два неколлинеарных вектора и образуют базис на
- 7. Базис на плоскости и в пространстве. Координаты вектора Разложить вектор по базису – значит представить его
- 8. Базис на плоскости и в пространстве. Координаты вектора Линейным операциям над векторами 8 и 1. 2.
- 9. Базис на плоскости и в пространстве. Координаты вектора Условия коллинеарности и компланарности векторов в координатной форме
- 10. Базис на плоскости и в пространстве. Координаты вектора Пример. Даны четыре вектора: 10 Показать, что три
- 11. Базис на плоскости и в пространстве. Координаты вектора Разложим четвертый вектор по этому базису: 11 Запишем
- 12. Базис на плоскости и в пространстве. Координаты вектора Запишем систему уравнений: 12
- 13. Базис на плоскости и в пространстве. Координаты вектора Осталось решить систему из 3-х уравнений на 3-и
- 14. Базис на плоскости и в пространстве. Координаты вектора 14
- 15. Скалярное произведение векторов. 15 Скалярным произведением векторов называют сумму произведений их координат: a·b=a1·b1+a2·b2+a3·b3 Скалярным произведением векторов
- 16. Скалярное произведение векторов. 16 С помощью скалярного произведения можно вычислить: Длину вектора: Расстояние между двумя точками:
- 17. Скалярное произведение векторов. 17 Условие перпендикулярности (ортогональности) векторов:
- 18. Свойства скалярного произведения векторов. 18 (критерий ортогональности векторов); 7. Работа силы , действующей на материальную точку
- 19. Векторное произведение. Векторным произведением двух векторов a и b называется вектор c такой, что: - модуль
- 20. Векторное произведение. Обозначение: 20 Координаты вектора вычисляются по формуле:
- 21. Свойства векторного произведения. 21 критерий коллинеарности векторов.
- 22. Смешанное произведение векторов. Смешанным произведением векторов 22 Абсолютная величина смешанного произведения векторов называется число: или равна
- 23. Свойства смешанного произведения. 23 - компланарны.
- 24. Примеры. Найти угол между векторами p и q, если p=2m+3n, q=m+2n, |m|=2, |n|=3, а угол между
- 25. Примеры. Теперь вычислим длину наших векторов: 25
- 26. Примеры. В результате получим: 26
- 27. Примеры. Найти векторное произведение векторов 27
- 28. Примеры. Вычислить смешанное произведение векторов 28
- 29. Аналитическая геометрия на плоскости. 29 1. Расстояние d между точками M1(x1,y1) и M2(x2,y2) на плоскости: 2.
- 30. Аналитическая геометрия на плоскости. 30 б) уравнение прямой с угловым коэффициентом - нормальный вектор прямой, 3.
- 31. Аналитическая геометрия на плоскости. 31 г) уравнение прямой, проходящей через две точки M1(x1,y1) и M2(x2,y2) д)
- 32. Аналитическая геометрия на плоскости. 4. Взаимное расположение двух прямых y=k1x+b1 и y=k2x+b2: а) угол между прямыми:
- 33. Аналитическая геометрия на плоскости. 33 б) признак параллельности двух прямых: k1=k2; в) признак перпендикулярности двух прямых:
- 34. Примеры. 34 Даны координаты вершин треугольника АВС: А(–2,1), В(2,9), С(-7,8). Hайти: 1) систему неравенств, определяющих множество
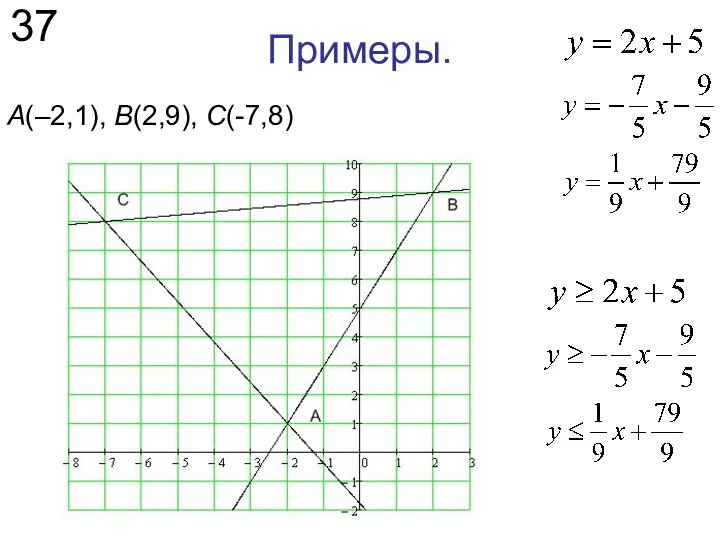
- 35. Примеры. 35 А(–2,1), В(2,9), С(-7,8)
- 36. Примеры. 36 А(–2,1), В(2,9), С(-7,8)
- 37. Примеры. 37 А(–2,1), В(2,9), С(-7,8)
- 38. Примеры. 38 Уравнения АС и ВС имеют вид: 2) угол С в радианах с точностью до
- 39. Примеры. 39 3) уравнение высоты AD и ее длину; Вспомним признак перпендикулярности прямых: В нашем случае
- 40. Примеры. Расстояние от точки до прямой вычисляется 40 А(–2,1)
- 41. Примеры. 4) уравнение медианы СE и координаты точки F пересечения этой медианы с высотой AD. Чтобы
- 42. Примеры. 42 С(-7,8), Е(0,5)
- 43. Примеры. 43 Для нахождения координат точки пересечения медианы и высоты, решим систем уравнений составленную их уравнения
- 44. Примеры. 44 5) уравнение окружности, для которой высота AD есть диаметр.
- 46. Скачать презентацию










































 презентация к уроку математики Число и цифра 5 1 класс умк гармония
презентация к уроку математики Число и цифра 5 1 класс умк гармония Перевод обыкновенной дроби в десятичную. Урок математики в 6 классе
Перевод обыкновенной дроби в десятичную. Урок математики в 6 классе Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник
Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения.
Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения. Приемы быстрого умножения
Приемы быстрого умножения Вычисление площадей плоских фигур. 11 класс
Вычисление площадей плоских фигур. 11 класс Интерактивное учебное пособие. Помоги Незнайке
Интерактивное учебное пособие. Помоги Незнайке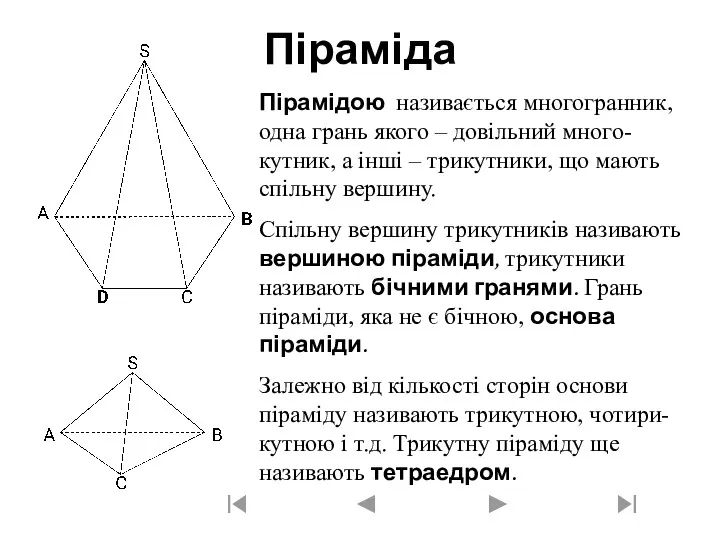 Многогранник піраміда
Многогранник піраміда Корень n-ной степени
Корень n-ной степени Графический метод решения квадратных неравенств
Графический метод решения квадратных неравенств Правило округления натуральных чисел
Правило округления натуральных чисел Теорема Пифагора
Теорема Пифагора Логарифмы и их свойства
Логарифмы и их свойства Веселая математика
Веселая математика Презентация Сказка о Маше и Веселой точке в стране Великой Математики
Презентация Сказка о Маше и Веселой точке в стране Великой Математики Подготовка к ЕГЭ по математике. Решение уравнений и неравенств задание В7
Подготовка к ЕГЭ по математике. Решение уравнений и неравенств задание В7 Элементы теории корреляции
Элементы теории корреляции Математика. Изучение нового материала.
Математика. Изучение нового материала. Прямоугольный параллелепипед
Прямоугольный параллелепипед Общие методы решения тригонометрических уравнений
Общие методы решения тригонометрических уравнений Виды углов
Виды углов Определение окружности, ее основных элементов
Определение окружности, ее основных элементов Решение логарифмических уравнений
Решение логарифмических уравнений Задача. Урок математики в 1 классе. Презентация к уроку.
Задача. Урок математики в 1 классе. Презентация к уроку. Перестановки, размещения, сочетания
Перестановки, размещения, сочетания Урок -викторина Счастливый случай. Параллельные прямые
Урок -викторина Счастливый случай. Параллельные прямые Коллинеарные векторы
Коллинеарные векторы