Содержание
- 2. Пусть G=(V, E) - граф. Цикл, который включает все ребра и вершины графа G, называется эйлеровым
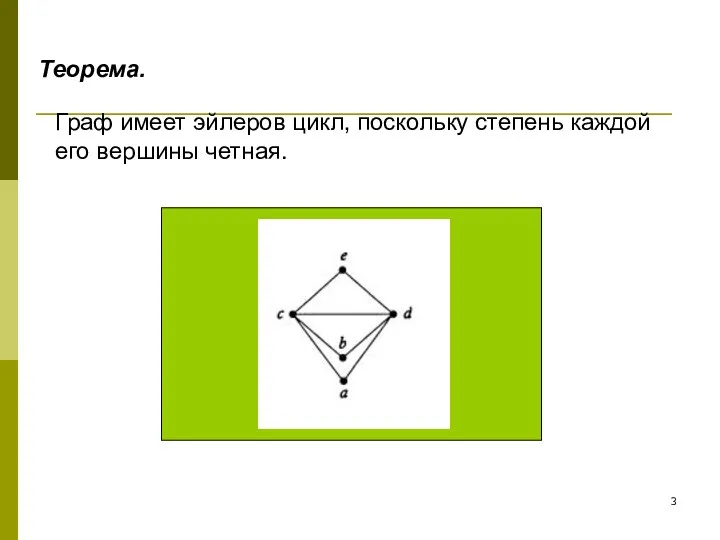
- 3. Граф имеет эйлеров цикл, поскольку степень каждой его вершины четная. Теорема.
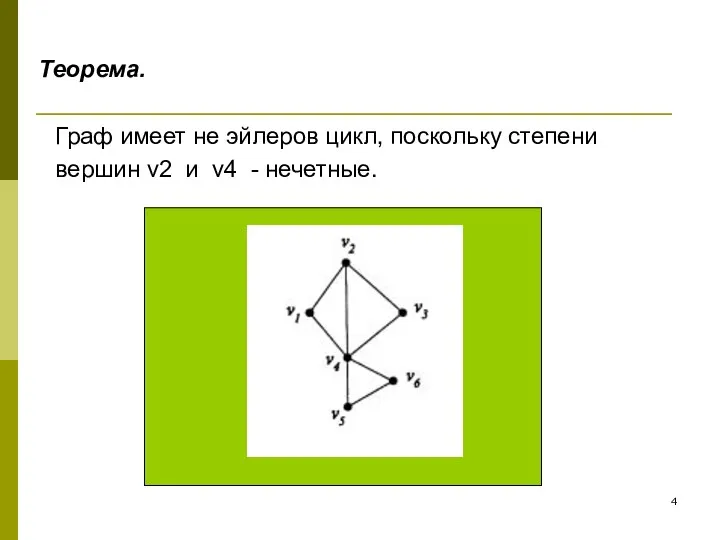
- 4. Граф имеет не эйлеров цикл, поскольку степени вершин v2 и v4 - нечетные. Теорема.
- 5. Пусть G=(V, E) – граф. Путь, который включает каждое ребро графа G только один раз называется
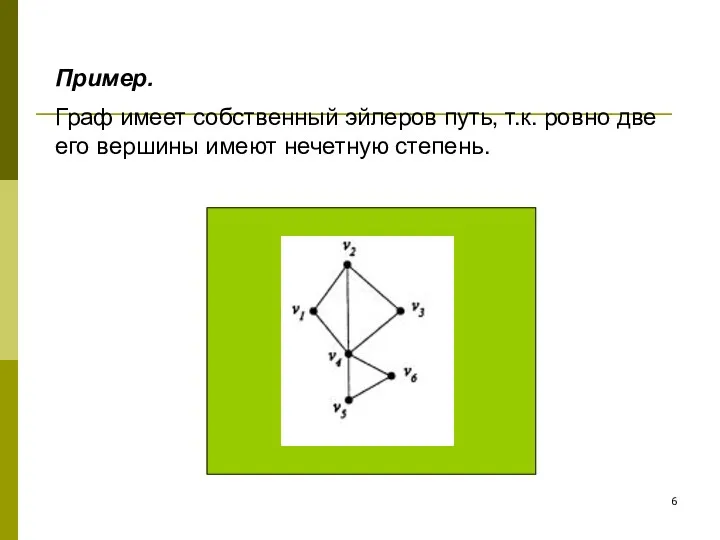
- 6. Граф имеет собственный эйлеров путь, т.к. ровно две его вершины имеют нечетную степень. Пример.
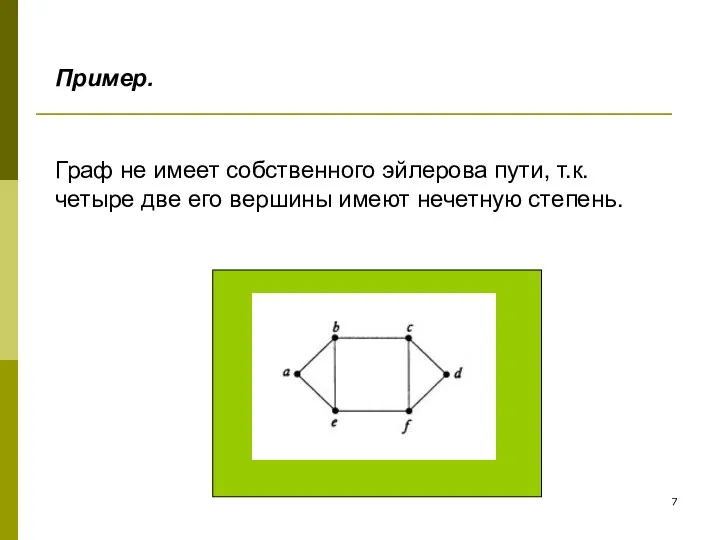
- 7. Граф не имеет собственного эйлерова пути, т.к. четыре две его вершины имеют нечетную степень. Пример.
- 8. Пусть G=(V, E) – ориентированный граф. Ориентированным циклом называется ориентированный путь ненулевой длины из вершины в
- 9. Определение. Вершина w орграфа D (графа G) достижима из вершины v, если либо v=w, либо существует
- 10. Определение. Орграф называется односторонне связным, если для любых его двух вершин, по крайней мере, одна достижима
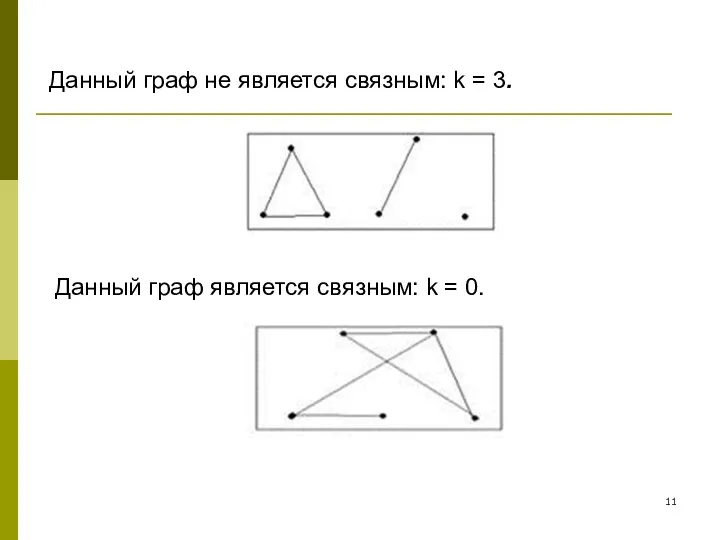
- 11. Данный граф является связным: k = 0. Данный граф не является связным: k = 3.
- 12. Пусть G – простой граф с n вершинами и k компонентами. Тогда число m его ребер
- 13. При исследовании графов возникает вопрос: насколько сильно связен связный граф? Этот вопрос можно сформулировать и так:
- 14. Определение. Разрезом называется такое разделяющее множество, никакое собственное подмножество которого не является разделяющим. Определение. Разрез, состоящий
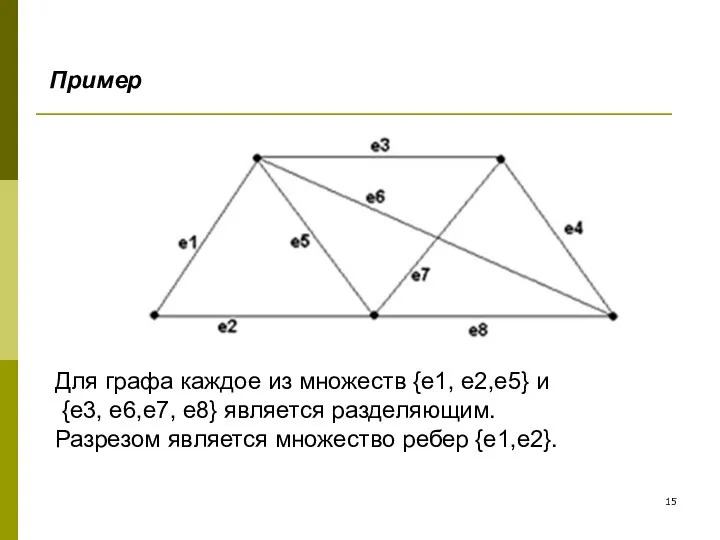
- 15. Для графа каждое из множеств {e1, e2,e5} и {e3, e6,e7, e8} является разделяющим. Разрезом является множество
- 16. Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и степень входа каждой
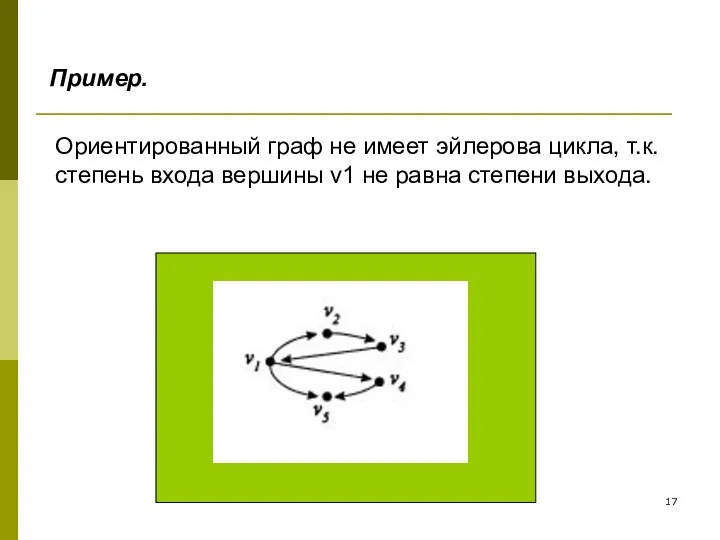
- 17. Ориентированный граф не имеет эйлерова цикла, т.к. степень входа вершины v1 не равна степени выхода. Пример.
- 18. Гиперкубы и код Грея
- 19. Определение: Расстояние между двумя вершинами графа называется длина самого короткого пути между этими двумя вершинами. Определение:
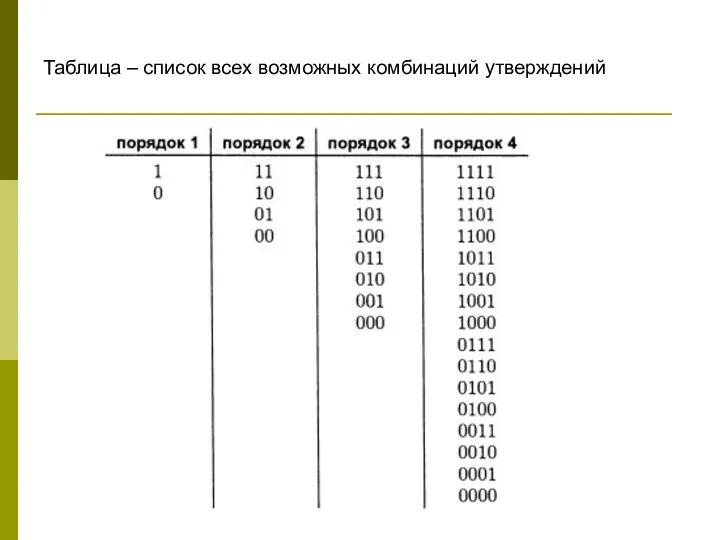
- 21. Таблица – список всех возможных комбинаций утверждений
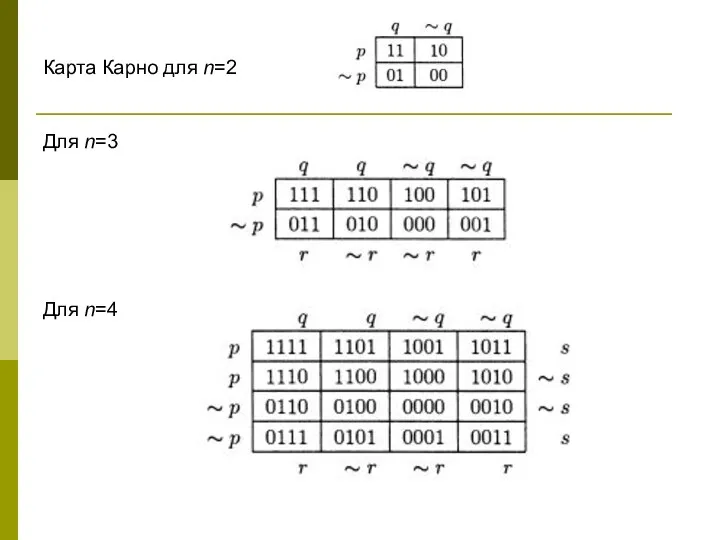
- 22. Карта Карно для n=2 Для n=3 Для n=4
- 23. Последовательность вершин для k+1 –мерного куба, используя последовательность вершин k –мерного куба: 1) Поместить 1 перед
- 24. Реверсируем список вершин для k –мерного куба, т.е. порядок вершин в списке изменим на обратный. Формирование
- 25. Список вершин для 3-мерного куба: Перейдем Приведенная процедура всегда будет давать последовательность вершин для k –мерного
- 26. Код Грея Правило построения кода Грея для k+1 : 1) Поместить 1 перед каждой вершиной в
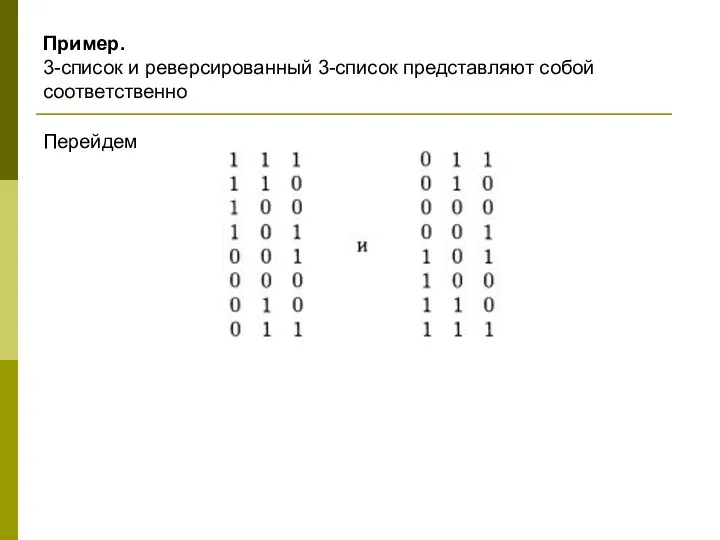
- 27. Пример. 3-список и реверсированный 3-список представляют собой соответственно Перейдем
- 28. Следовательно, код Грея для n=4
- 29. Соединение компьютеров в конфигурацию сетки или решета. Сетка – граф, вершины которого заданы массивом размерности m×n
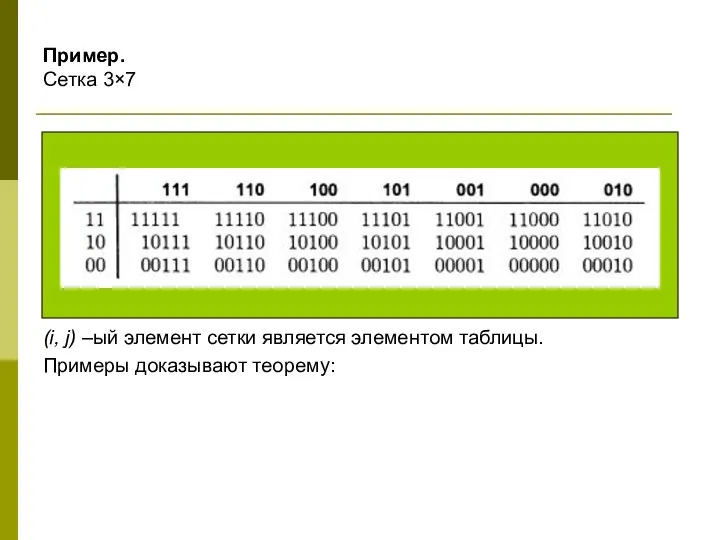
- 30. Пример. Сетка 3×7 (i, j) –ый элемент сетки является элементом таблицы. Примеры доказывают теорему:
- 31. Теорема Каждая сетка размера m×n представляет собой подграф i + j -мерного куба, где m≤ 2i
- 32. Теорема Каждый гиперкуб для n ≥ 1 является двудольным графом, в котором непересекающиеся множества вершин состоят
- 34. Скачать презентацию




















 Пифагор и теоремы. Интересные факты из жизни Пифагора
Пифагор и теоремы. Интересные факты из жизни Пифагора Средняя линия треугольника
Средняя линия треугольника урок математики
урок математики Суретте тікбұрышты параллелепипед бейнеленген
Суретте тікбұрышты параллелепипед бейнеленген Миллион
Миллион Геодезия. Определение площадей
Геодезия. Определение площадей Измерение углов. Транспортир
Измерение углов. Транспортир Сложение и вычитание многочленов. 7 класс
Сложение и вычитание многочленов. 7 класс Нахождение доли числа и числа по его доле
Нахождение доли числа и числа по его доле Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Математикалық балық аулау. Тренажер
Математикалық балық аулау. Тренажер Модуль Геометрия. ОГЭ-2017
Модуль Геометрия. ОГЭ-2017 Измерение отрезков
Измерение отрезков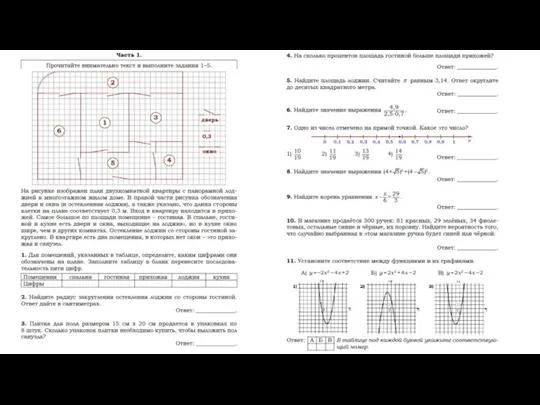 Задания по математике. Вариант 4
Задания по математике. Вариант 4 Краткий запись задач 1 клас
Краткий запись задач 1 клас Алгебраические дроби (урок повторения и обобщения). 8 класс
Алгебраические дроби (урок повторения и обобщения). 8 класс Поиски неизвестного количества
Поиски неизвестного количества уравнение
уравнение Методическое пособие. Разработка урока по математике. 4 класс.
Методическое пособие. Разработка урока по математике. 4 класс. Геометрические фигуры (2 класс)
Геометрические фигуры (2 класс) Многочлены. Действия с многочленами
Многочлены. Действия с многочленами Действия с дробями. Умножение дробей
Действия с дробями. Умножение дробей Понятие движения
Понятие движения Производные элементарных функций
Производные элементарных функций Простейшие преобразования графиков функций
Простейшие преобразования графиков функций Графики косинуса
Графики косинуса Урок математики
Урок математики Координатная плоскость. 6 класс
Координатная плоскость. 6 класс