Содержание
- 2. Пусть функция y=f(x) - непрерывная на отрезке [a;b] , причём на этом отрезке f(x) ≥ 0
- 3. 2.Площадь криволинейной трапеции. SABCDE =? 0 y x a b A B C D E S1
- 4. Определённый интеграл ∫f(x)dx = а b Нижний предел интегрирования Верхний предел интегрирования Рассмотрим непрерывную на некотором
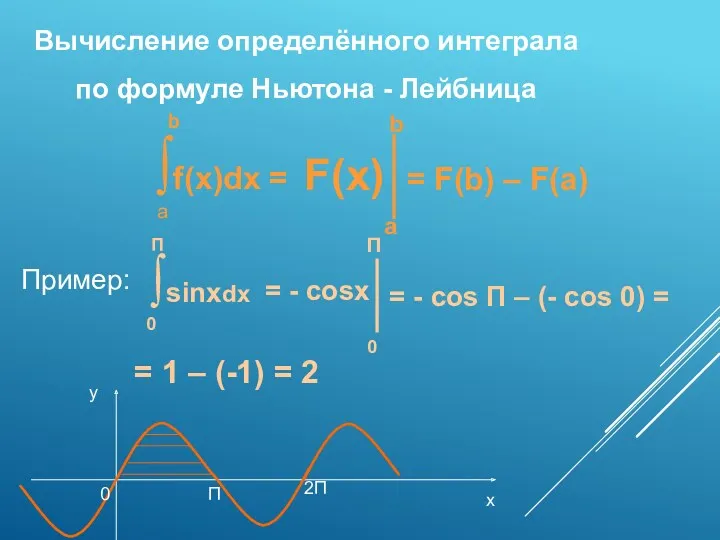
- 5. Вычисление определённого интеграла по формуле Ньютона - Лейбница ∫f(x)dx = а b F(x) a b =
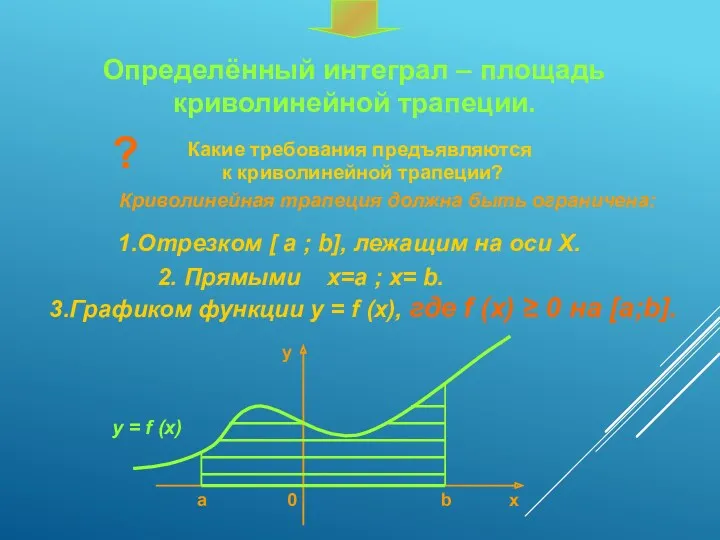
- 6. Определённый интеграл – площадь криволинейной трапеции. ? Какие требования предъявляются к криволинейной трапеции? Криволинейная трапеция должна
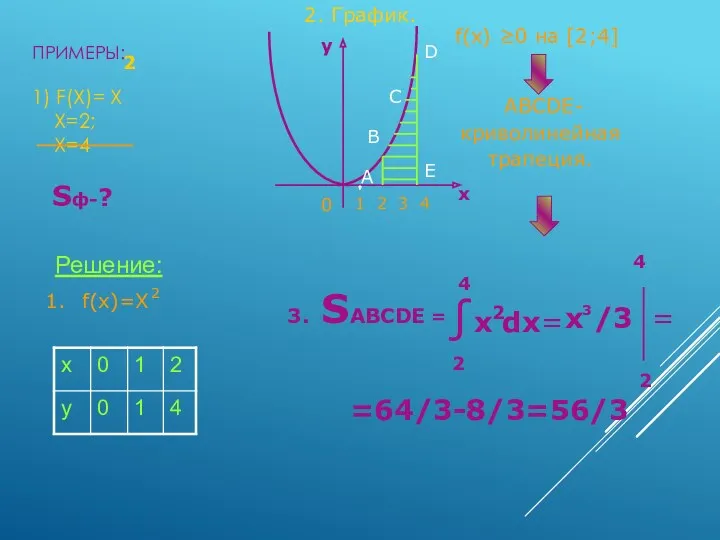
- 7. ПРИМЕРЫ: 1) F(X)= X X=2; X=4 2 Sф-? Решение: f(x)=X 2 2. График. y x 0
- 8. 3.Вычисление площадей фигур с помощью интеграла. а) Пусть фигура ограничена графиком непрерывной функции y= f(x), причём
- 9. Задачи по готовым чертежам: 2. График. 0 y x 1 2 3 4 0 4 4
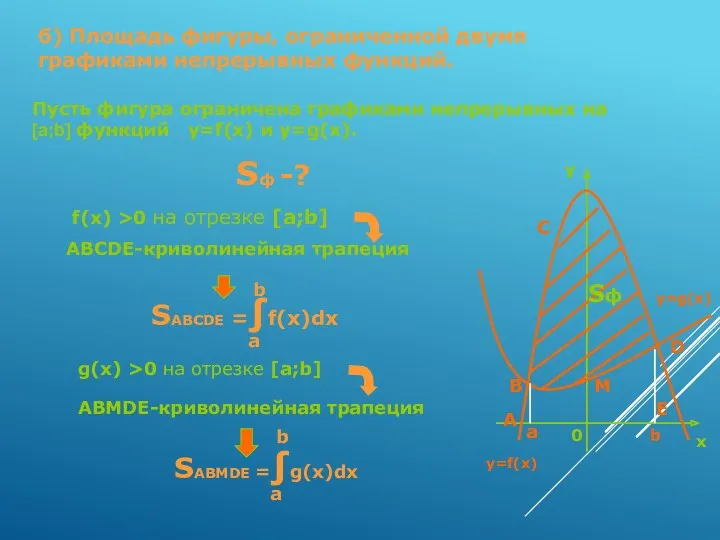
- 10. б) Площадь фигуры, ограниченной двумя графиками непрерывных функций. Пусть фигура ограничена графиками непрерывных на [a;b] функций
- 11. Sф -? y x 0 y=g(x) y=f(x) A B C D a b Sф E SABMDE
- 12. y x 0 Дано: f(x) = (x – 2)²; g(x)= - (х-2)² + 2 ; S
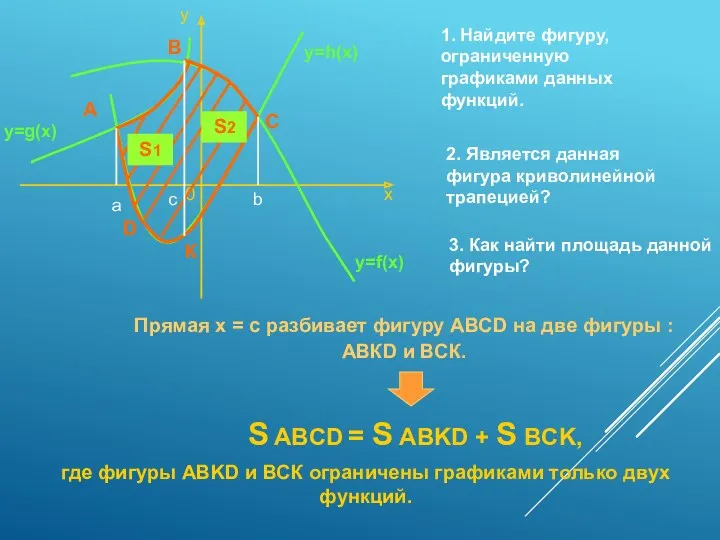
- 13. у х 0 y=f(x) y=g(x) y=h(x) 1. Найдите фигуру, ограниченную графиками данных функций. 2. Является данная
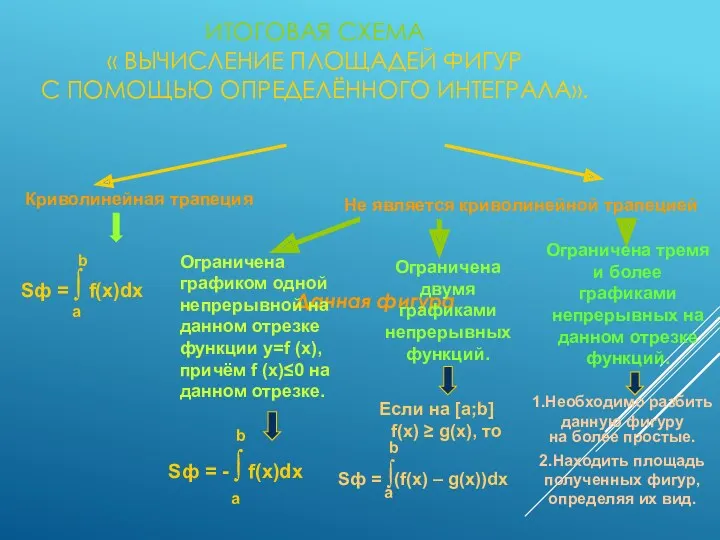
- 14. ИТОГОВАЯ СХЕМА « ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА». Данная фигура Криволинейная трапеция Не является
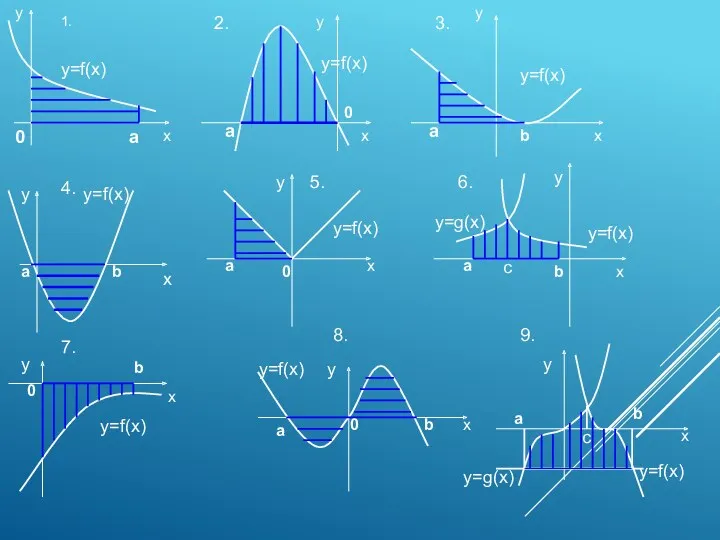
- 15. Самостоятельная работа На предложенных далее рисунках изображены различные фигуры. 1. Выберете из них те, на которых
- 16. 1. 2. 3. 4. 5. 6. 7. 8. 9. 0 а у х у х у
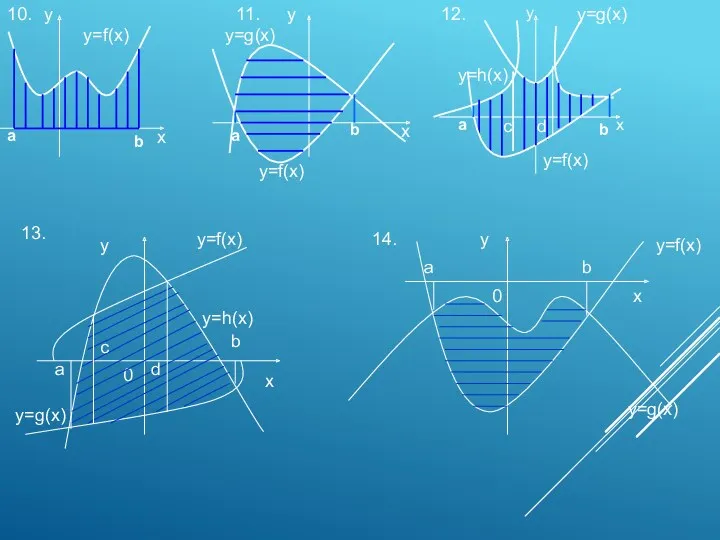
- 17. 10. 11. 12. x y y x y x a b a b a b у=f(x)
- 19. Скачать презентацию
![Пусть функция y=f(x) - непрерывная на отрезке [a;b] , причём](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/315053/slide-1.jpg)







 урок математики на тему Распределительное свойство умножения
урок математики на тему Распределительное свойство умножения Зачем будущим банковским работникам математика
Зачем будущим банковским работникам математика Ключевые задачи в процессе обучения школьников решению задач по геометрии
Ключевые задачи в процессе обучения школьников решению задач по геометрии Что называется процентом?
Что называется процентом? Закрепление пройденного материала
Закрепление пройденного материала Презентация по занятию ФЭМПОстров сокровищ
Презентация по занятию ФЭМПОстров сокровищ Сравнение чисел
Сравнение чисел Корень n-й степени. Упражнение 9
Корень n-й степени. Упражнение 9 Магия чисел
Магия чисел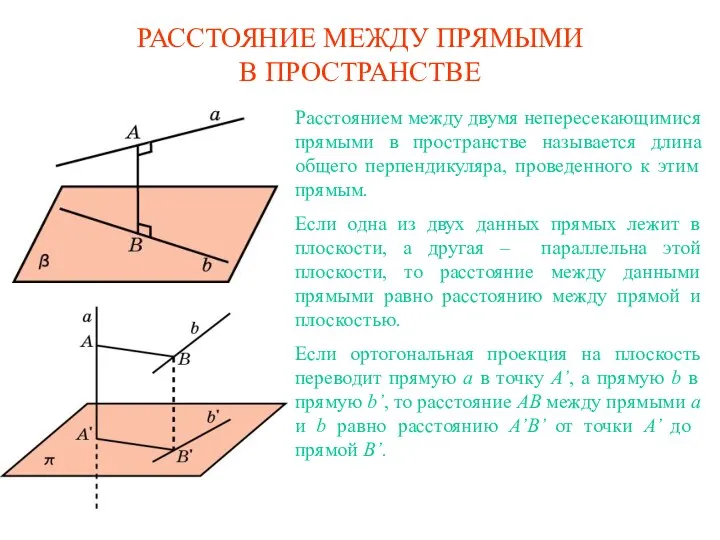 Расстояние между прямыми в пространстве
Расстояние между прямыми в пространстве Случаи сложения вида +4
Случаи сложения вида +4 Связь между компонентами и результатом умножения. Решение задач
Связь между компонентами и результатом умножения. Решение задач Геометрическое место точек. Окружность и круг
Геометрическое место точек. Окружность и круг Расстояние между параллельными прямыми
Расстояние между параллельными прямыми Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация Вычитание
Презентация Вычитание Прибавление и вычитание числа 2
Прибавление и вычитание числа 2 Средняя линия треугольника
Средняя линия треугольника Решение уравнений sinx=a. Понятие арксинуса числа
Решение уравнений sinx=a. Понятие арксинуса числа Письменное деление на трёхзначное число
Письменное деление на трёхзначное число Геометрические тела. Черчение
Геометрические тела. Черчение Прямоугольник
Прямоугольник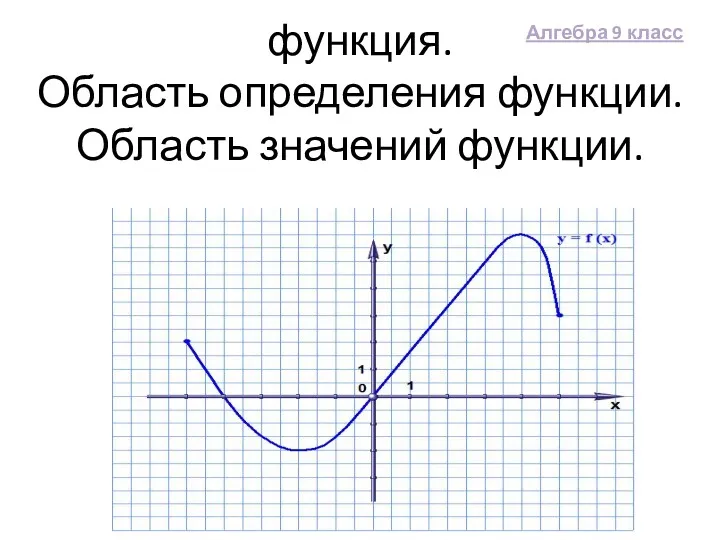 Функция. Область определения функции. Область значений функции. Алгебра 9 класс
Функция. Область определения функции. Область значений функции. Алгебра 9 класс Достоверные, невозможные и случайные события
Достоверные, невозможные и случайные события Натуральные числа. Урок-сказка
Натуральные числа. Урок-сказка Закрепление изученного. Решение задач.
Закрепление изученного. Решение задач. презентация к уроку математики в 4 классе Палетка Школа России
презентация к уроку математики в 4 классе Палетка Школа России Треугольники. Тест
Треугольники. Тест