Содержание
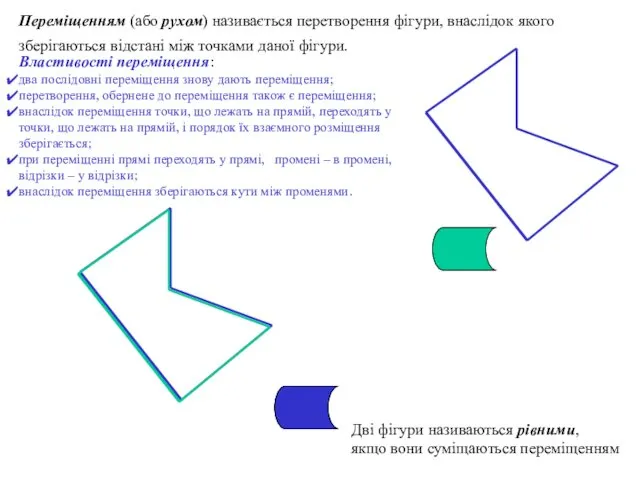
- 2. Переміщенням (або рухом) називається перетворення фігури, внаслідок якого зберігаються відстані між точками даної фігури. Дві фігури
- 3. Паралельним перенесенням фігури F у напрямі променя ОА на відстань а називається таке перетворення фігури F
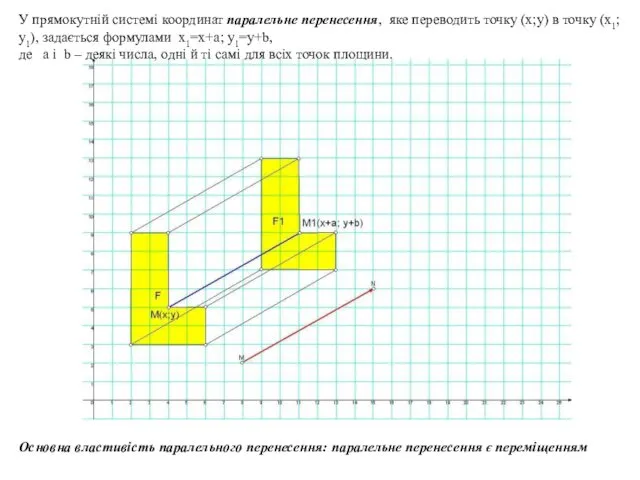
- 4. Основна властивість паралельного перенесення: паралельне перенесення є переміщенням У прямокутній системі координат паралельне перенесення, яке переводить
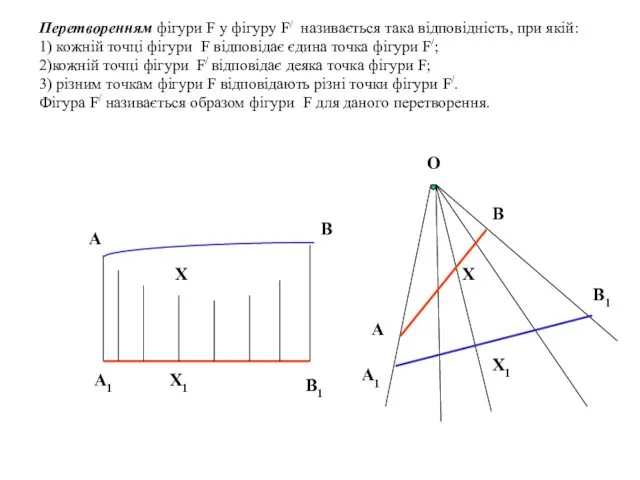
- 5. Перетворенням фігури F у фігуру F/ називається така відповідність, при якій: 1) кожній точці фігури F
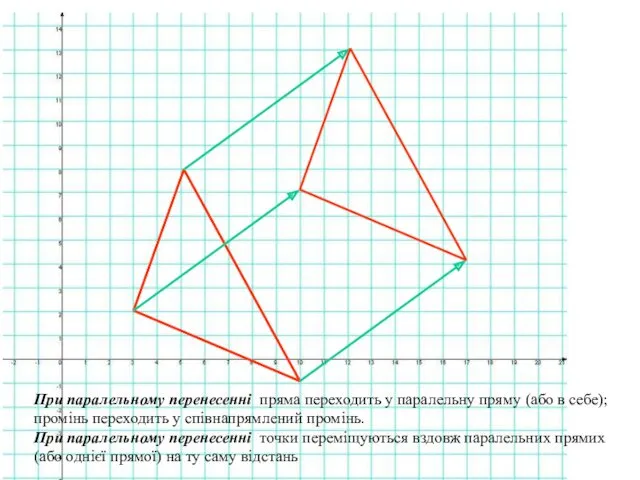
- 6. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе); промінь переходить у співнапрямлений промінь.
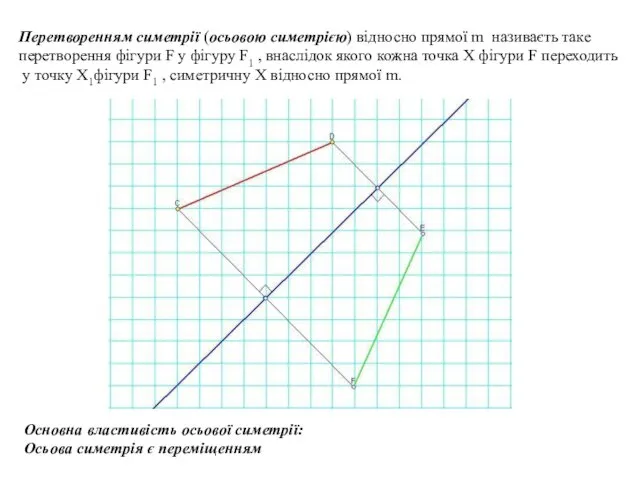
- 7. Перетворенням симетрії (осьовою симетрією) відносно прямої m називаєть таке перетворення фігури F у фігуру F1 ,
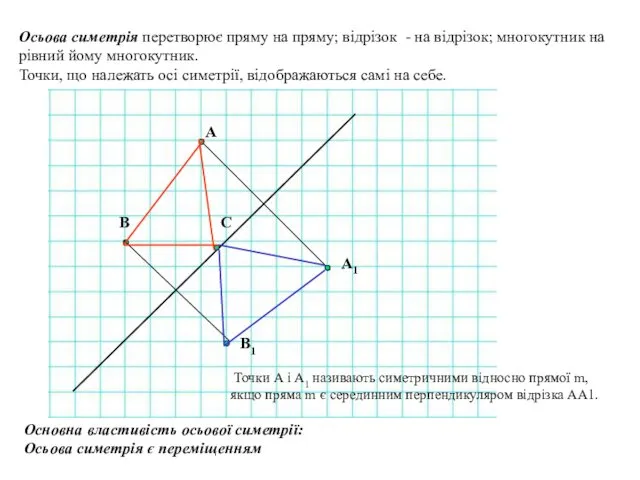
- 8. Осьова симетрія перетворює пряму на пряму; відрізок - на відрізок; многокутник на рівний йому многокутник. Точки,
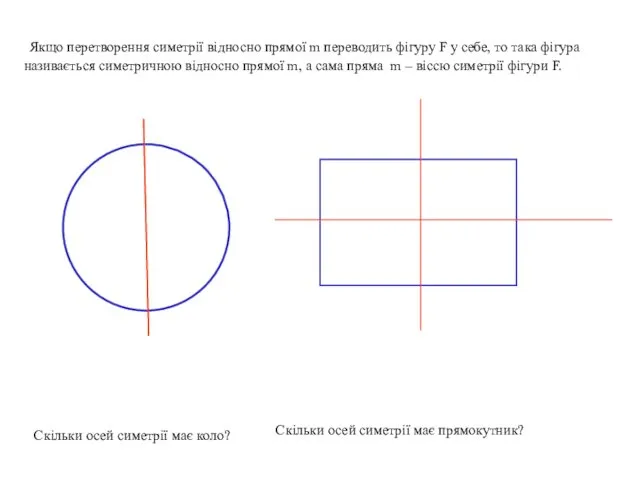
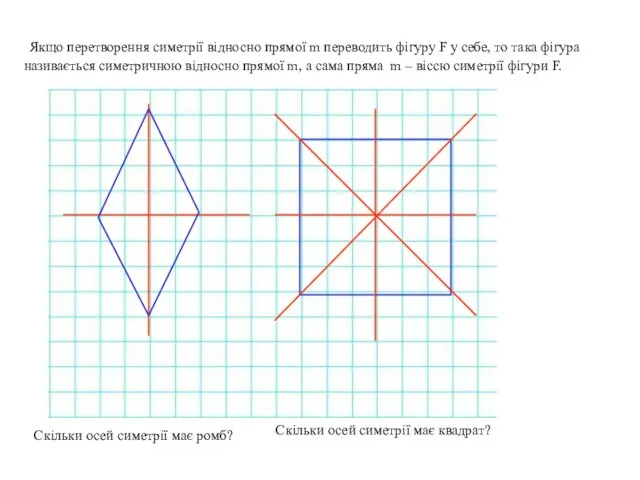
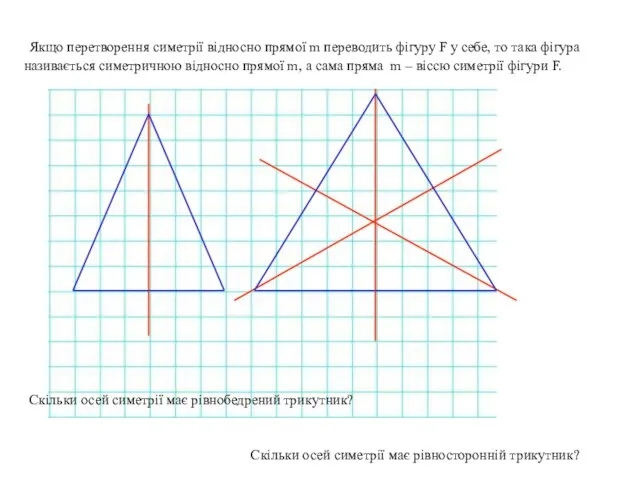
- 9. Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною
- 10. Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною
- 11. Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною
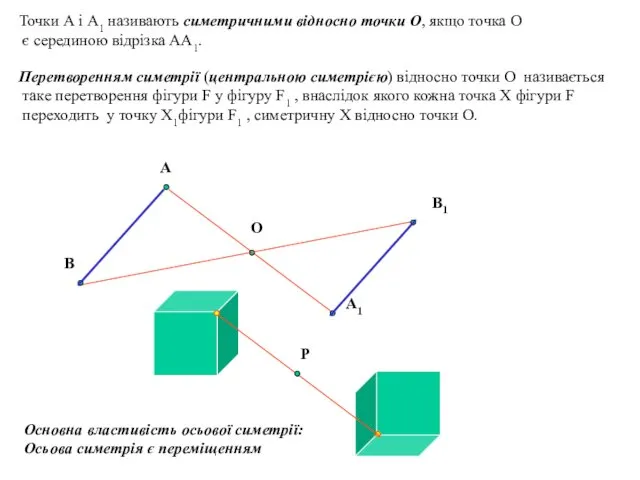
- 12. Точки А і А1 називають симетричними відносно точки О, якщо точка О є серединою відрізка АА1.
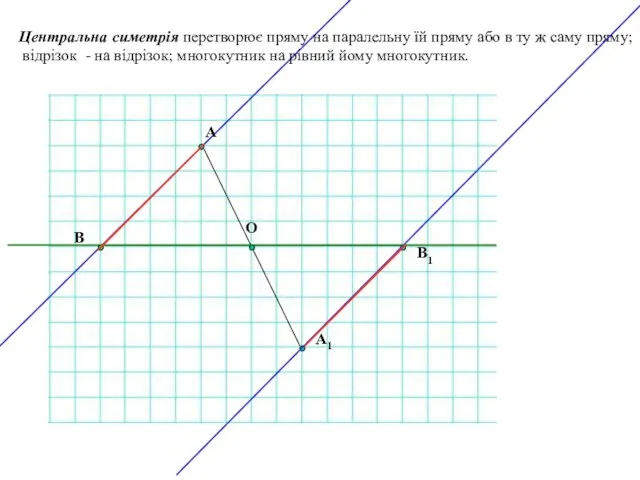
- 13. Центральна симетрія перетворює пряму на паралельну їй пряму або в ту ж саму пряму; відрізок -
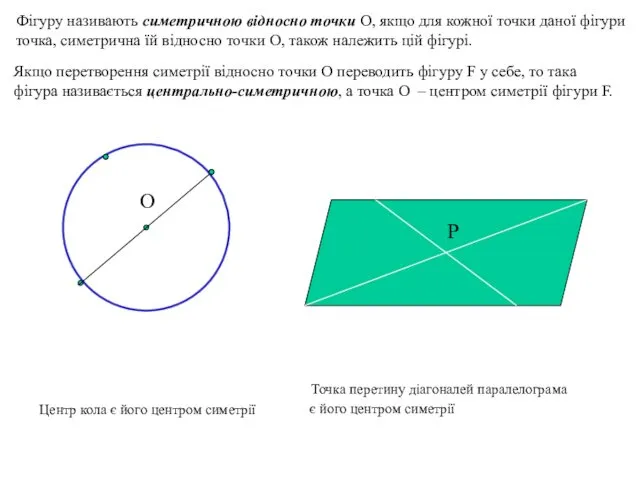
- 14. Фігуру називають симетричною відносно точки О, якщо для кожної точки даної фігури точка, симетрична їй відносно
- 15. Поворотом фігури F навколо точки О на кут α називається перетворення фігури F у фігуру F1
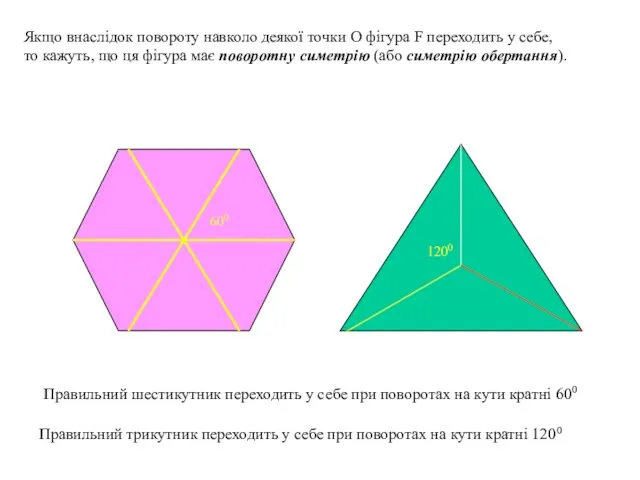
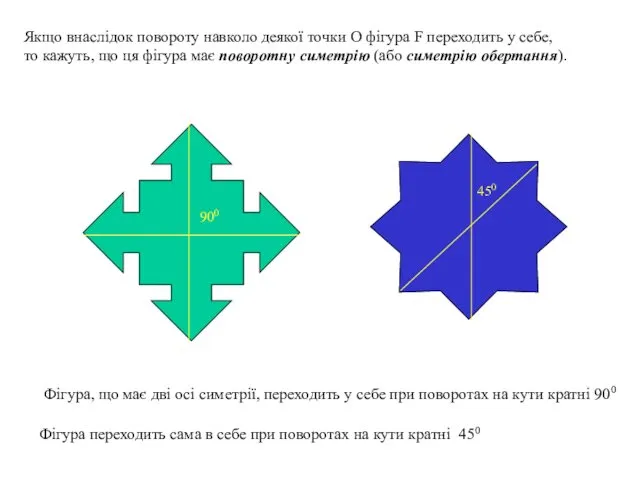
- 16. Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть, що ця
- 17. Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть, що ця
- 18. Перетворенням подібності (подібністю) називається таке перетворення фігури F у фігуру F1 , внаслідок якого відстані між
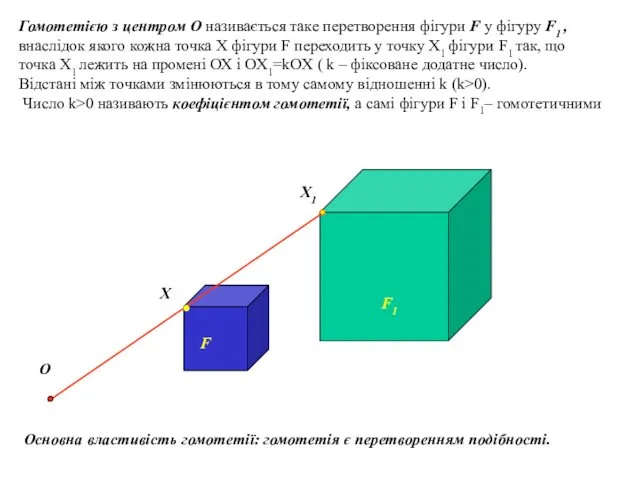
- 19. Гомотетією з центром О називається таке перетворення фігури F у фігуру F1 , внаслідок якого кожна
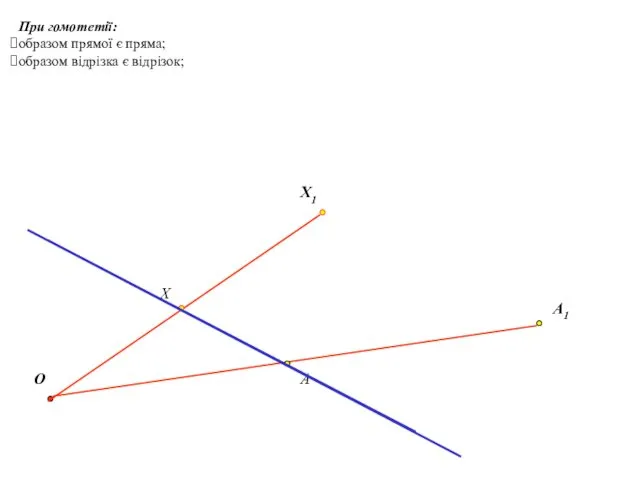
- 20. При гомотетії: образом прямої є пряма; образом відрізка є відрізок; O Х Х1 A A1
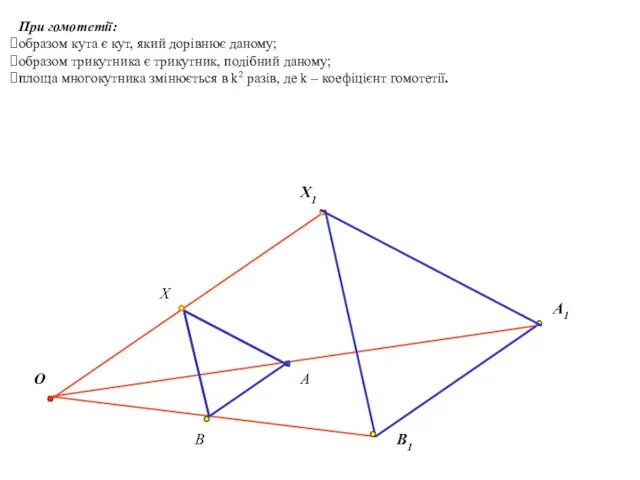
- 21. При гомотетії: образом кута є кут, який дорівнює даному; образом трикутника є трикутник, подібний даному; площа
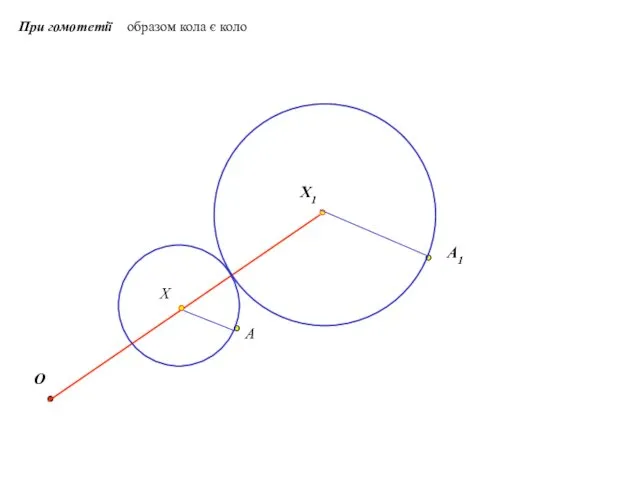
- 22. При гомотетії образом кола є коло O Х Х1 A A1
- 24. Скачать презентацию



 Давайте посчитаем. Устный счёт. 2класс. Математика
Давайте посчитаем. Устный счёт. 2класс. Математика Единица измерения сантиметр
Единица измерения сантиметр Задачи на чертежах по теме трапеция
Задачи на чертежах по теме трапеция Подготовка к ЕГЭ по математике. Профильная группа В10, база В4
Подготовка к ЕГЭ по математике. Профильная группа В10, база В4 Урок математики 2 класс УМК Школа 2100 и мастер класс Использование компьютерных технологий
Урок математики 2 класс УМК Школа 2100 и мастер класс Использование компьютерных технологий Сложение и вычитание в пределах 10
Сложение и вычитание в пределах 10 Евклидово пространство
Евклидово пространство Самостоятельные работы по математике. 4 класс.
Самостоятельные работы по математике. 4 класс. Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. 8 класс Тест по математике +3, -3 , 1 класс.
Тест по математике +3, -3 , 1 класс. Приёмы быстрого счёта
Приёмы быстрого счёта Основы статистики. Статистика & Биостатистика
Основы статистики. Статистика & Биостатистика Отношение двух чисел. Работа с математической моделью
Отношение двух чисел. Работа с математической моделью Угол. Измерение углов. Виды углов
Угол. Измерение углов. Виды углов Презентация Решение задач (СДО)
Презентация Решение задач (СДО) Векторы
Векторы Урок математики по УМК Перспективная начальная школа 2 класс,четвёртая четверть. Урок-путешествие в королевство Задачи Диск
Урок математики по УМК Перспективная начальная школа 2 класс,четвёртая четверть. Урок-путешествие в королевство Задачи Диск Построение параболы
Построение параболы Десятичные дроби
Десятичные дроби Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания
Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания Площадь треугольника
Площадь треугольника Математика. 1 класс. Урок 69. Уравнение - Презентация
Математика. 1 класс. Урок 69. Уравнение - Презентация Многогранники
Многогранники Сравнение полощадей (система Эльконина - Давыдова) Диск
Сравнение полощадей (система Эльконина - Давыдова) Диск Великие математики и их открытия
Великие математики и их открытия Линейная функция. Решение задач
Линейная функция. Решение задач Итоговый тест по математике 2 класс
Итоговый тест по математике 2 класс Порядок выполнения действий в выражениях
Порядок выполнения действий в выражениях