Содержание
- 2. Четырёхугольники
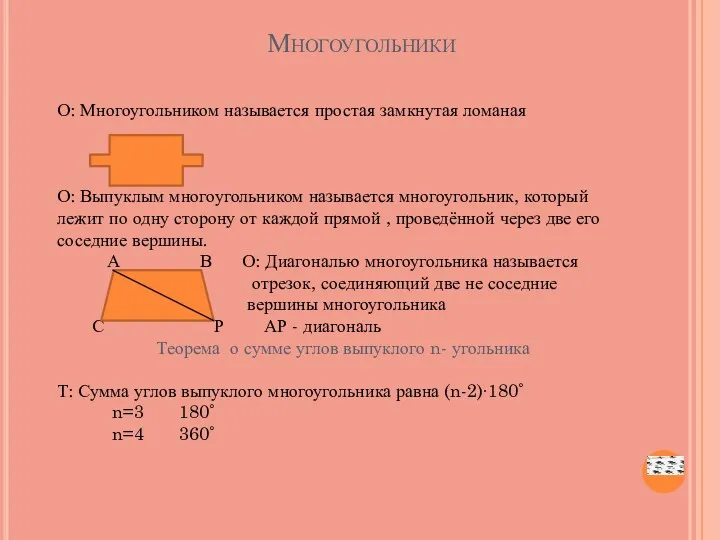
- 3. Многоугольники О: Многоугольником называется простая замкнутая ломаная О: Выпуклым многоугольником называется многоугольник, который лежит по одну
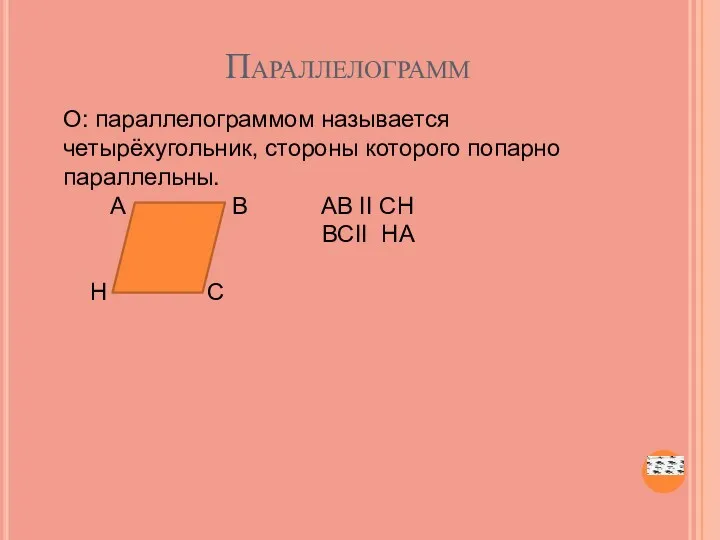
- 4. Параллелограмм О: параллелограммом называется четырёхугольник, стороны которого попарно параллельны. А В АВ ΙΙ СН ВСΙΙ НА
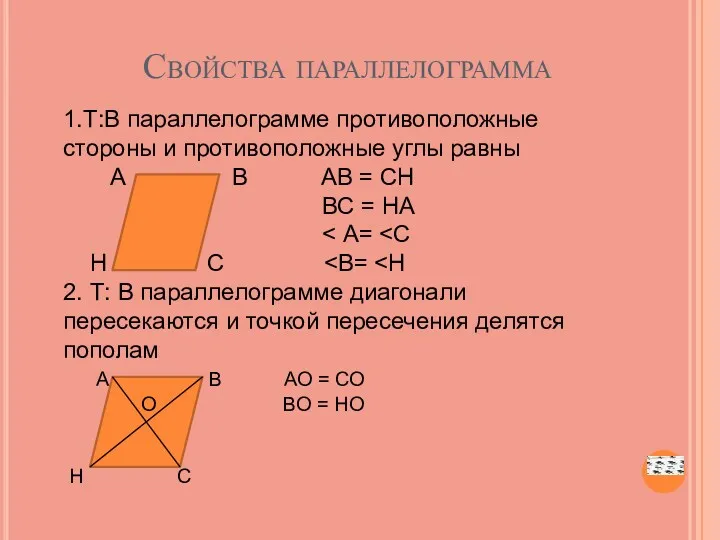
- 5. Свойства параллелограмма 1.Т:В параллелограмме противоположные стороны и противоположные углы равны А В АВ = СН ВС
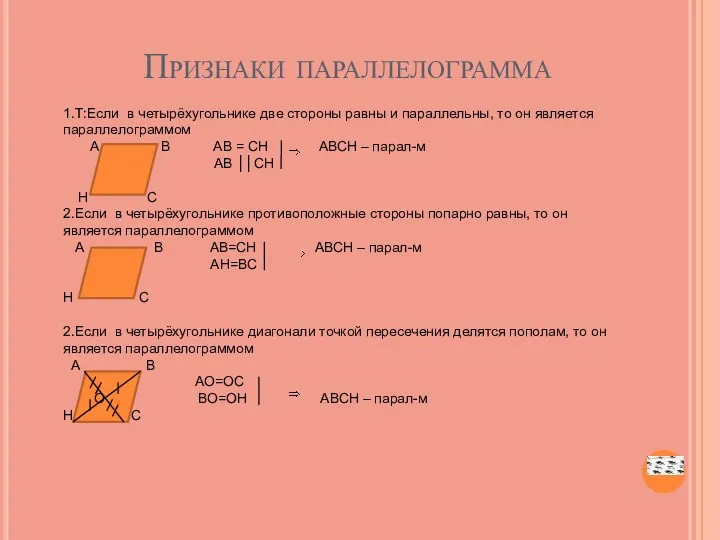
- 6. Признаки параллелограмма 1.Т:Если в четырёхугольнике две стороны равны и параллельны, то он является параллелограммом А В
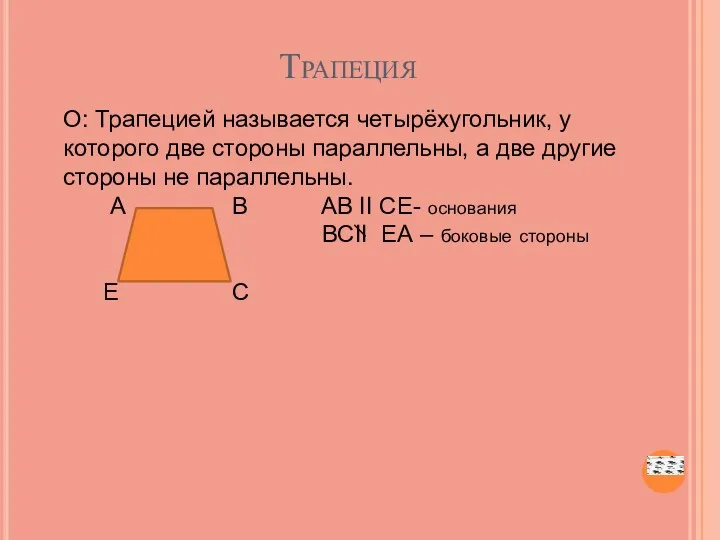
- 7. Трапеция О: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
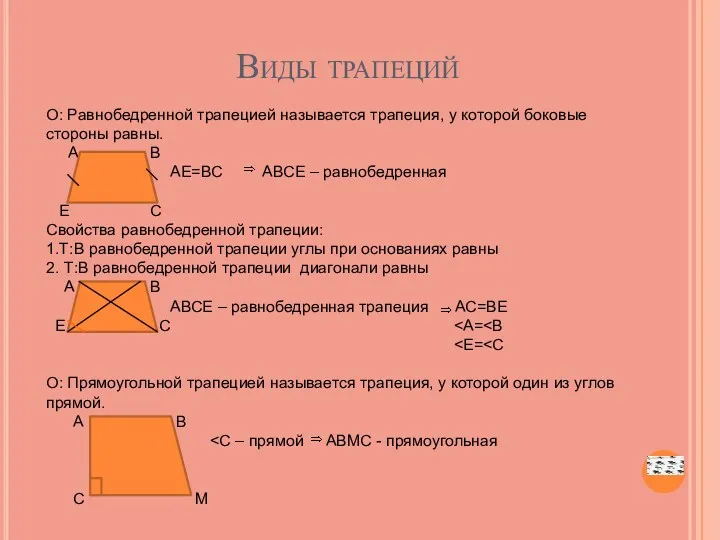
- 8. Виды трапеций О: Равнобедренной трапецией называется трапеция, у которой боковые стороны равны. А В АЕ=ВС АВСЕ
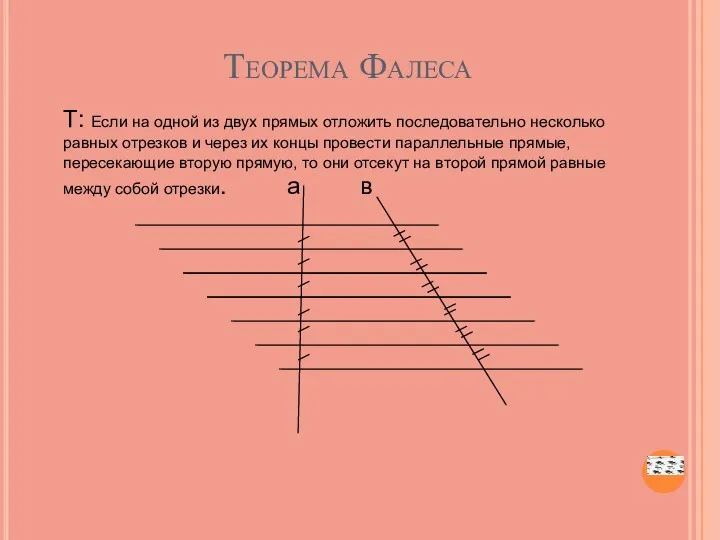
- 9. Теорема Фалеса Т: Если на одной из двух прямых отложить последовательно несколько равных отрезков и через
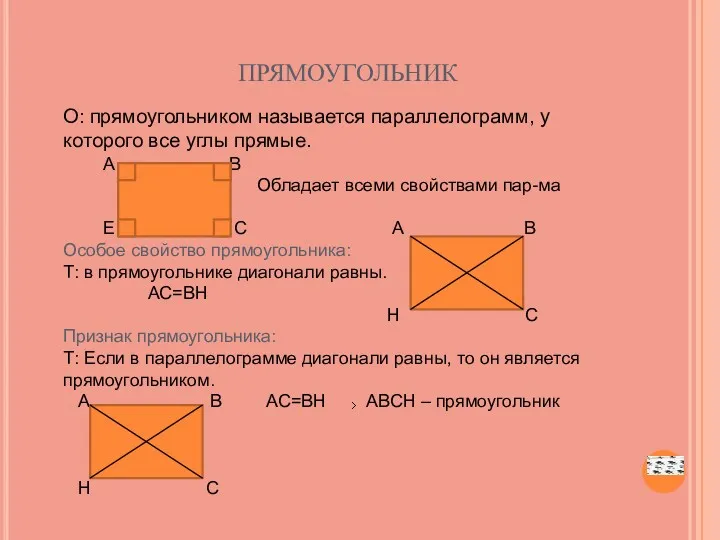
- 10. прямоугольник О: прямоугольником называется параллелограмм, у которого все углы прямые. А В Обладает всеми свойствами пар-ма
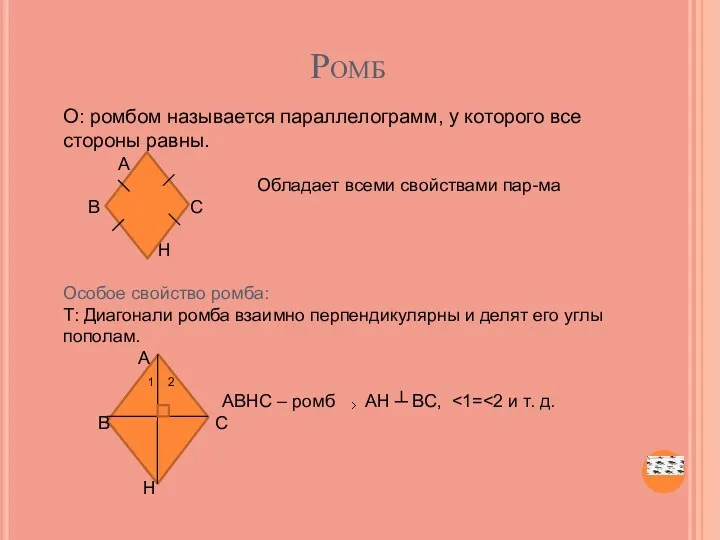
- 11. Ромб О: ромбом называется параллелограмм, у которого все стороны равны. А Обладает всеми свойствами пар-ма В
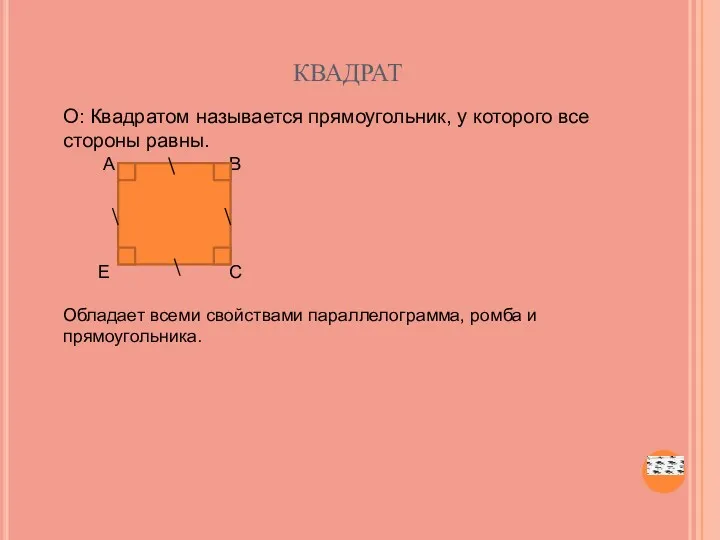
- 12. квадрат О: Квадратом называется прямоугольник, у которого все стороны равны. А В Е С Обладает всеми
- 13. Осевая симметрия О: Две точки А и В называются симметричными относительно прямой а, если эта прямая
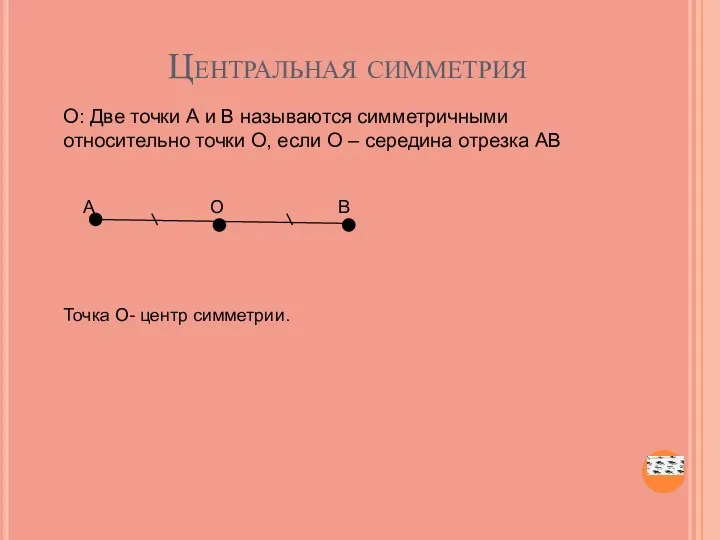
- 14. Центральная симметрия О: Две точки А и В называются симметричными относительно точки О, если О –
- 15. Площадь
- 16. Свойства площадей Т: Равные многоугольники имеют равные площади 2.Т: Если многоугольник составлен из нескольких многоугольников, то
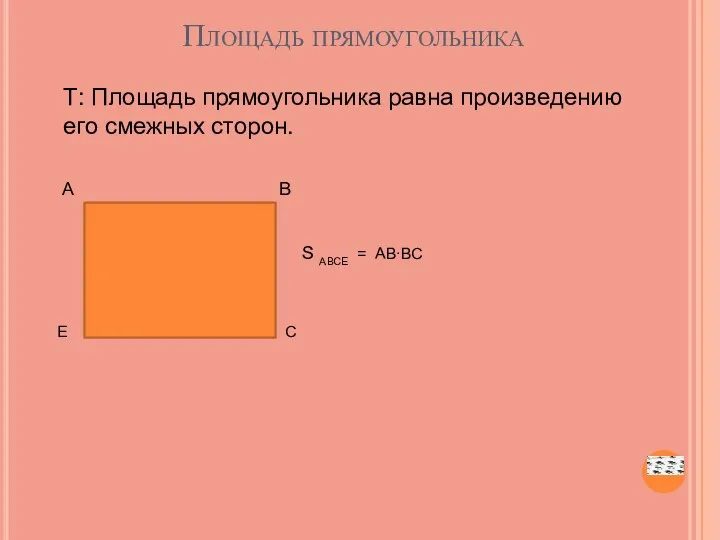
- 17. Площадь прямоугольника Т: Площадь прямоугольника равна произведению его смежных сторон. А В S АВСЕ = АВ∙ВС
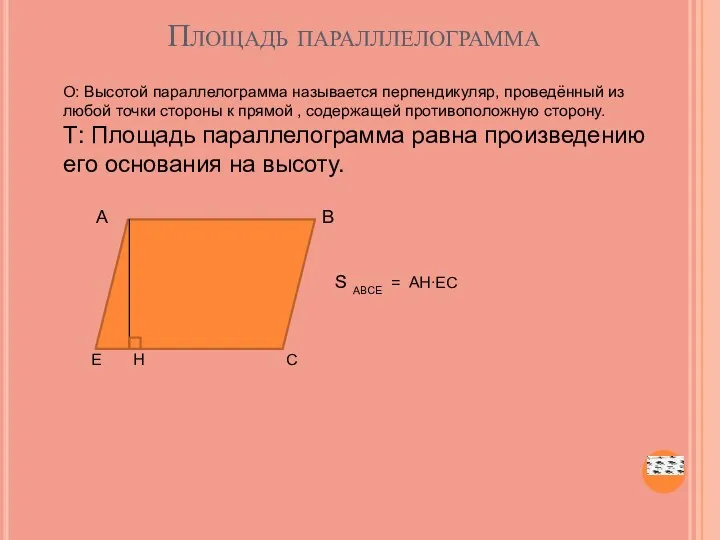
- 18. Площадь паралллелограмма О: Высотой параллелограмма называется перпендикуляр, проведённый из любой точки стороны к прямой , содержащей
- 19. Площадь треугольника Т: Площадь треугольника равна половине произведения его основания на высоту. В S ВСЕ =
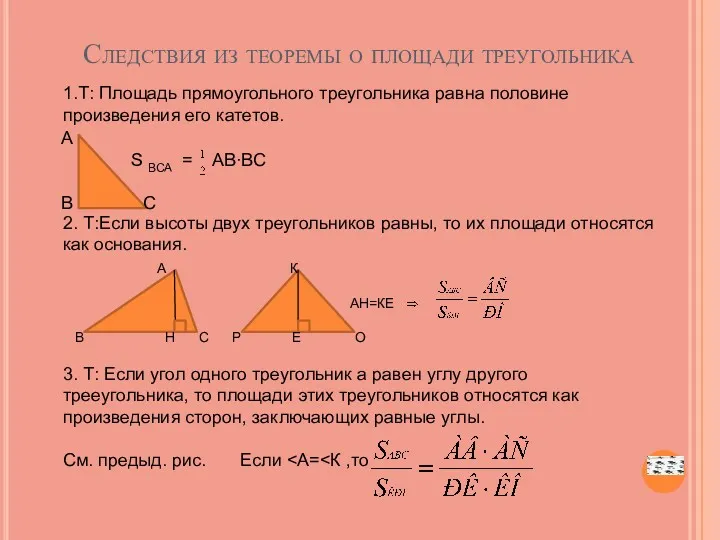
- 20. Следствия из теоремы о площади треугольника 1.Т: Площадь прямоугольного треугольника равна половине произведения его катетов. 2.
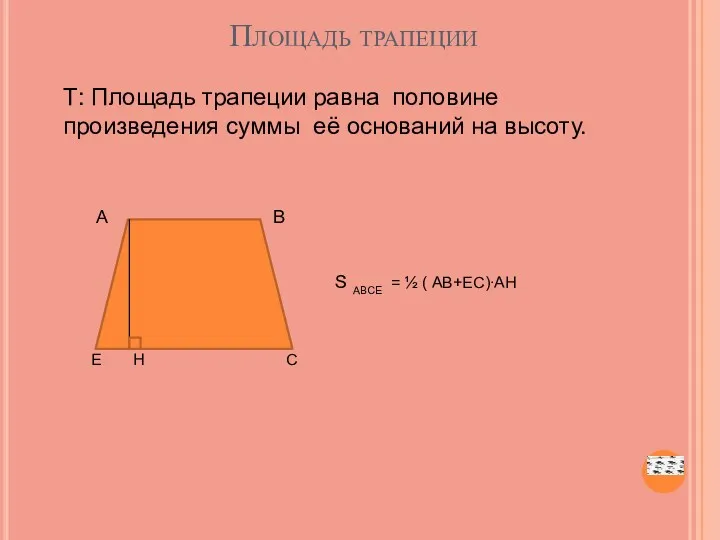
- 21. Площадь трапеции Т: Площадь трапеции равна половине произведения суммы её оснований на высоту. А В S
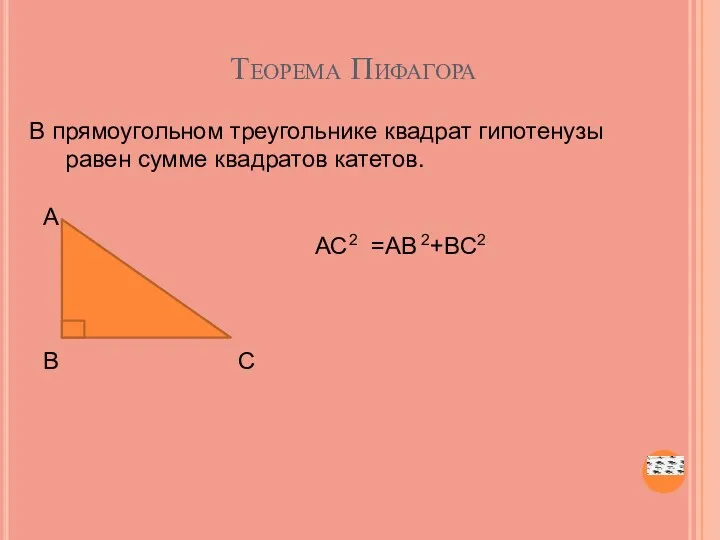
- 22. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А АС2 =АВ 2+ВС2 В
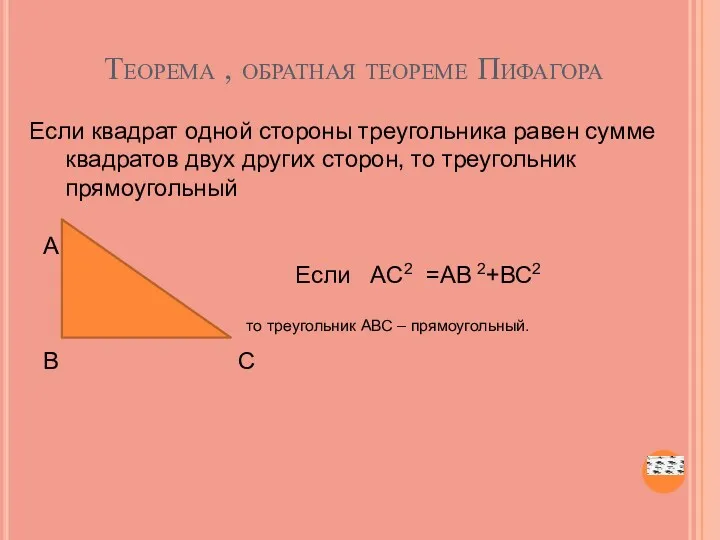
- 23. Теорема , обратная теореме Пифагора Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон,
- 24. Подобные треугольники
- 25. Пропорциональные отрезки О: Отношением отрезков АВ и НЕ называется отношение их длин. О: Отрезки АВ и
- 26. Подобные треугольники. О:Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны
- 27. Свойства подобных треугольников. 1.Т: Отношение периметров двух подобных треугольников равно коэффициенту подобия. ∆ АВС ∆А1В1С1 2.
- 28. Первый признак подобия треугольников. Т:если два угла одного треугольника равны двум углам другого треугольника, то такие
- 29. Второй признак подобия треугольников. Т:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы,
- 30. Третий признак подобия треугольников. Т:если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники являются
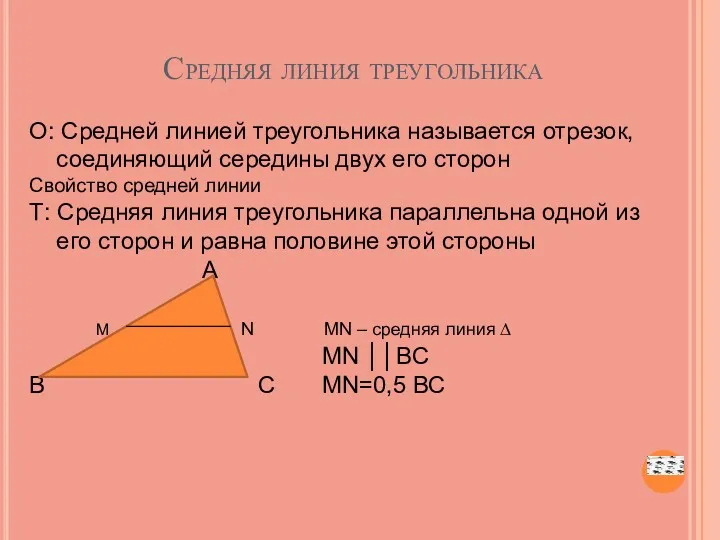
- 31. Средняя линия треугольника О: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон Свойство средней
- 32. Пропорциональные отрезки в прямоугольном треугольнике 1.Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное
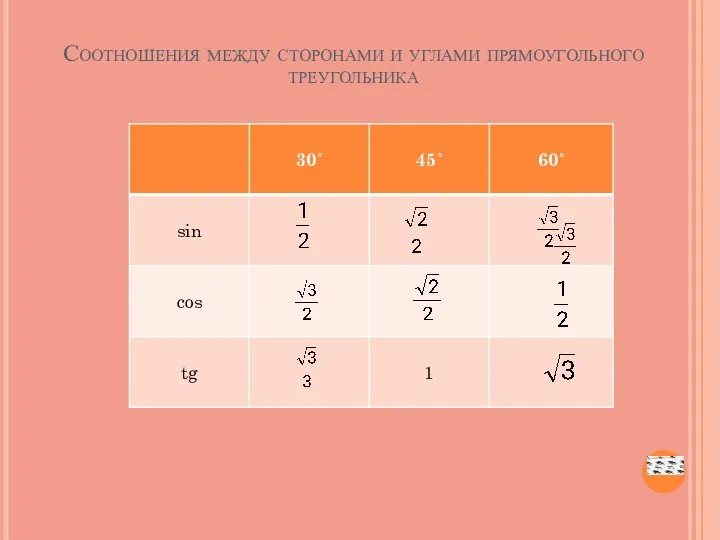
- 33. Соотношения между сторонами и углами прямоугольного треугольника О: синусом острого угла прямоугольного треугольника называется отношение противолежащего
- 34. Соотношения между сторонами и углами прямоугольного треугольника 1. 2. 3. Если сумма двух углов равна 90˚,
- 35. Соотношения между сторонами и углами прямоугольного треугольника Чтобы найти катет прямоугольного треугольника, можно: Гипотенузу умножить на
- 36. Соотношения между сторонами и углами прямоугольного треугольника
- 37. Окружность
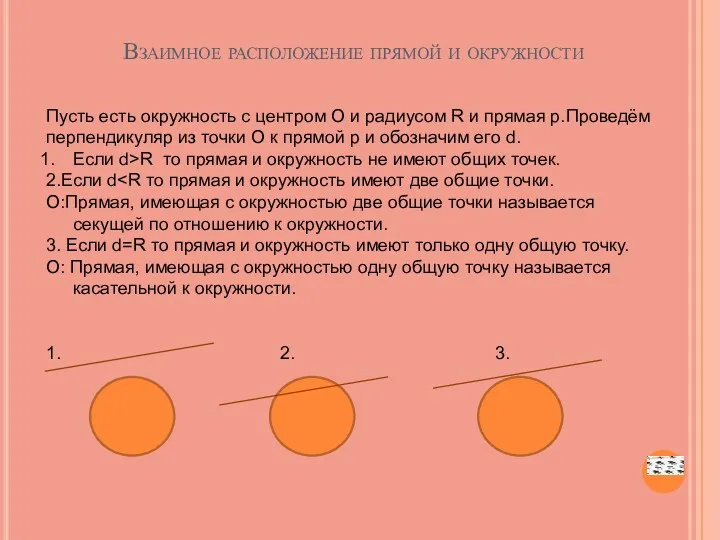
- 38. Взаимное расположение прямой и окружности Пусть есть окружность с центром О и радиусом R и прямая
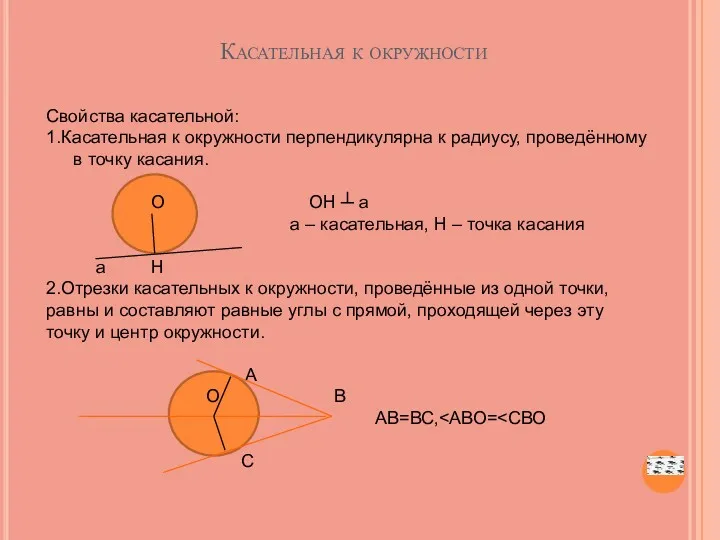
- 39. Касательная к окружности Свойства касательной: 1.Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. О
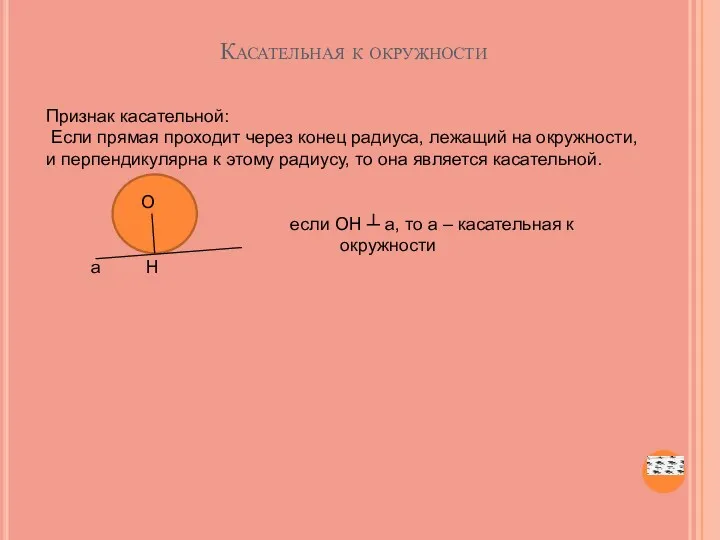
- 40. Касательная к окружности Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна
- 41. Градусная мера дуги окружности K L О:Дугой называется часть окружности, ограниченная двумя точками. Две точки A
- 42. Центральный угол О: Центральным углом называется угол, вершина которого находится в центре окружности K A B
- 43. Вписанный угол О: Вписанным углом называется угол, вершина которого лежит на окружности K A O В
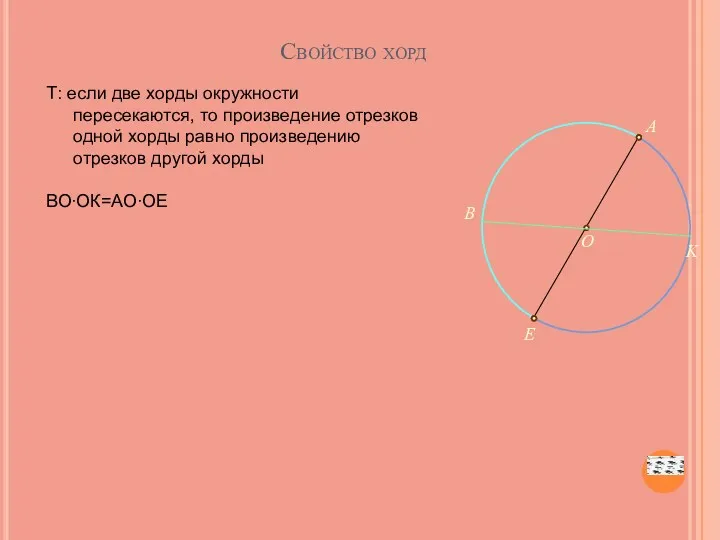
- 44. Свойство хорд Т: если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков
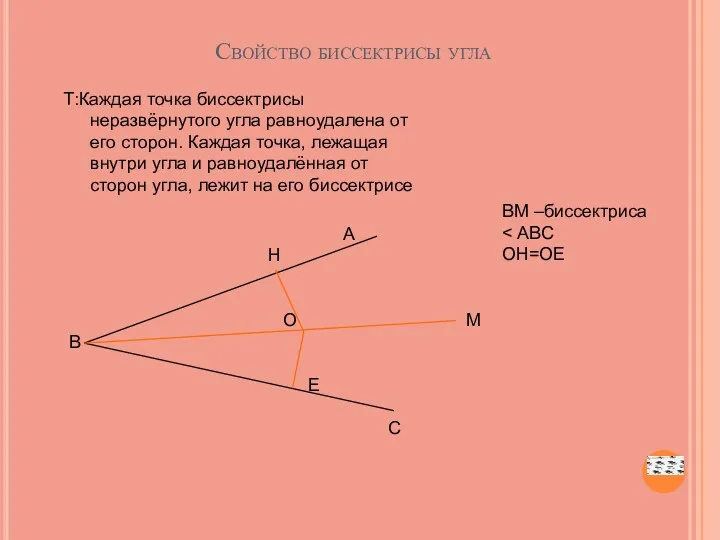
- 45. А Н О М В Е С Свойство биссектрисы угла Т:Каждая точка биссектрисы неразвёрнутого угла равноудалена
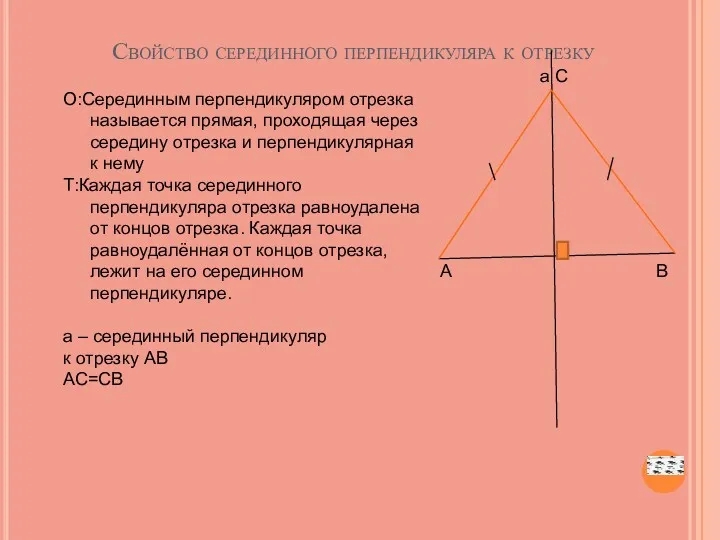
- 46. а С А В Свойство серединного перпендикуляра к отрезку О:Серединным перпендикуляром отрезка называется прямая, проходящая через
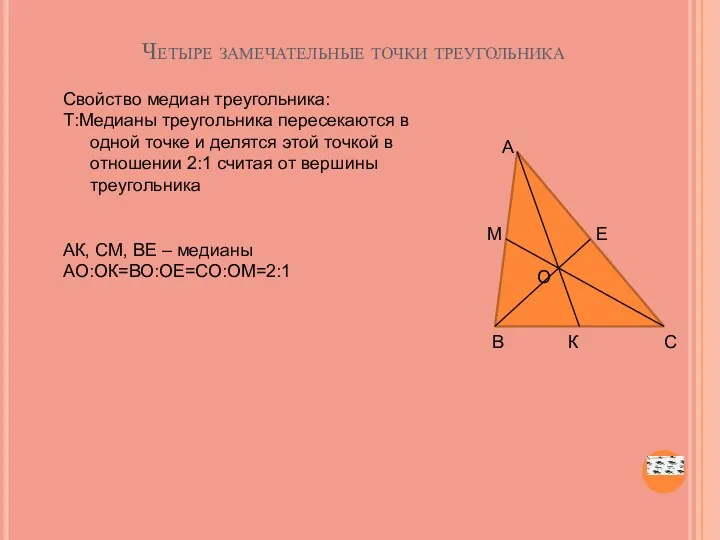
- 47. Четыре замечательные точки треугольника Свойство медиан треугольника: Т:Медианы треугольника пересекаются в одной точке и делятся этой
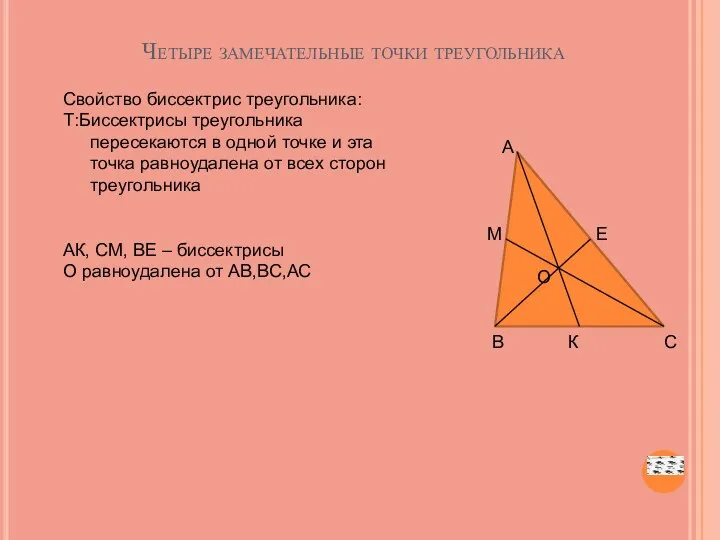
- 48. Четыре замечательные точки треугольника Свойство биссектрис треугольника: Т:Биссектрисы треугольника пересекаются в одной точке и эта точка
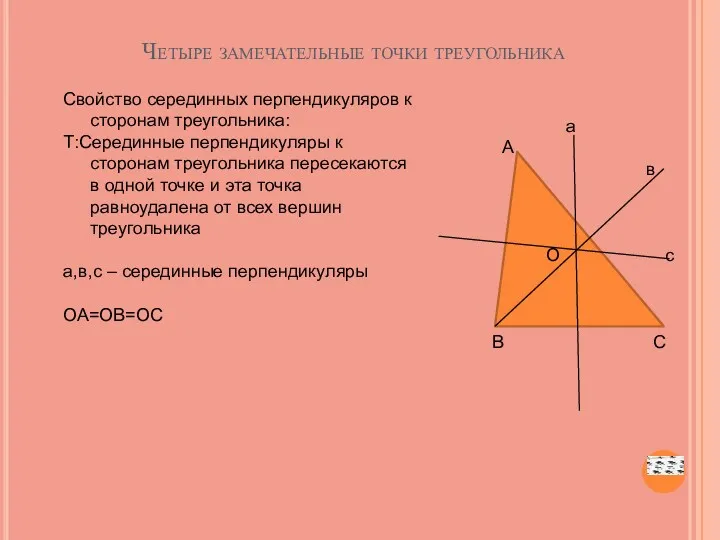
- 49. Четыре замечательные точки треугольника Свойство серединных перпендикуляров к сторонам треугольника: Т:Серединные перпендикуляры к сторонам треугольника пересекаются
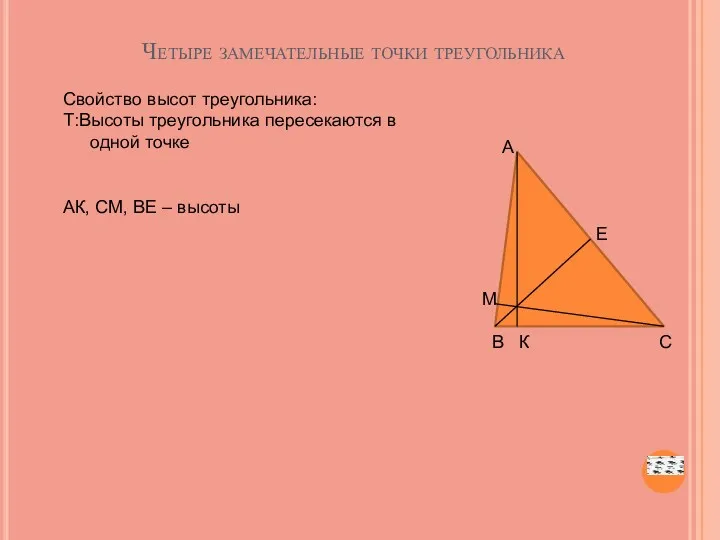
- 50. А Е О М В К С Четыре замечательные точки треугольника Свойство высот треугольника: Т:Высоты треугольника
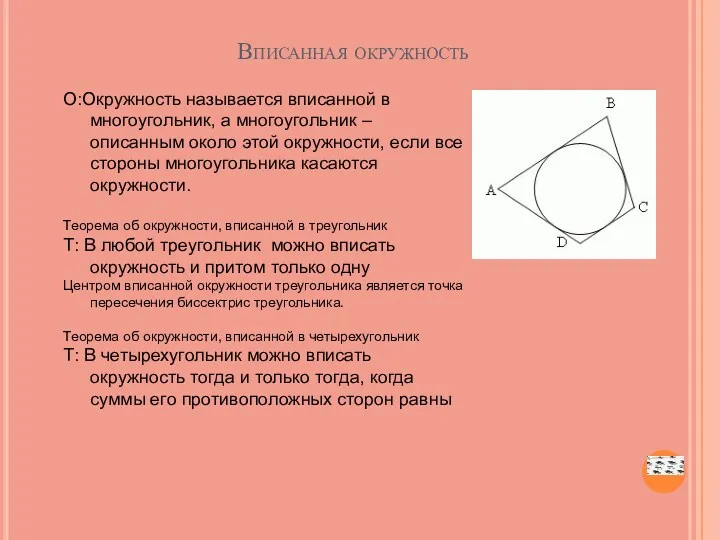
- 51. Вписанная окружность О:Окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности, если все
- 53. Скачать презентацию




















 Цилиндр. Основные сведения
Цилиндр. Основные сведения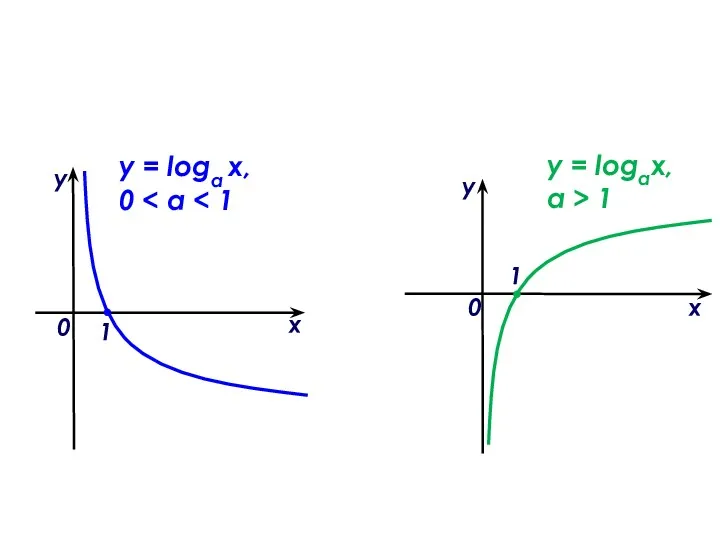 Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Названия чисел в записи действий (2 класс)
Названия чисел в записи действий (2 класс) Практикум по решению задачи 20. ЕГЭ базовый уровень
Практикум по решению задачи 20. ЕГЭ базовый уровень Прямая и обратная пропорциональная зависимости
Прямая и обратная пропорциональная зависимости C_26
C_26 Производные и интегралы функций общего вида
Производные и интегралы функций общего вида Первый признак равенства треугольников
Первый признак равенства треугольников Анализ учебников математики 1-4 классов
Анализ учебников математики 1-4 классов Треугольники. Основные признаки и свойства треугольников
Треугольники. Основные признаки и свойства треугольников Центральные и вписанные углы. 8 класс
Центральные и вписанные углы. 8 класс Признаки параллельности прямых. Решение задач на применение признаков параллельности прямых
Признаки параллельности прямых. Решение задач на применение признаков параллельности прямых Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Квадратные неравенства (8 класс)
Квадратные неравенства (8 класс) Интерактивные тесты по математике
Интерактивные тесты по математике Формулы сокращенного умножения
Формулы сокращенного умножения Случаи вычитания 11-
Случаи вычитания 11- Основное свойство дробей
Основное свойство дробей Инженерная графика. Начертательная геометрия. Конспект лекций
Инженерная графика. Начертательная геометрия. Конспект лекций Краткий справочный материал по математике для студентов 1 курса
Краткий справочный материал по математике для студентов 1 курса Признаки делимости натуральных чисел
Признаки делимости натуральных чисел Делители и кратные. Урок для обучающиеся 6 класса
Делители и кратные. Урок для обучающиеся 6 класса Сложение и вычитание в пределах 100. Таблица умножения
Сложение и вычитание в пределах 100. Таблица умножения Граф. Связный граф. Представление задачи с помощью графа
Граф. Связный граф. Представление задачи с помощью графа Пространственные фигуры
Пространственные фигуры Математика. 1 класс. Урок 98. Сложение и вычитание в пределах 20 - Презентация
Математика. 1 класс. Урок 98. Сложение и вычитание в пределах 20 - Презентация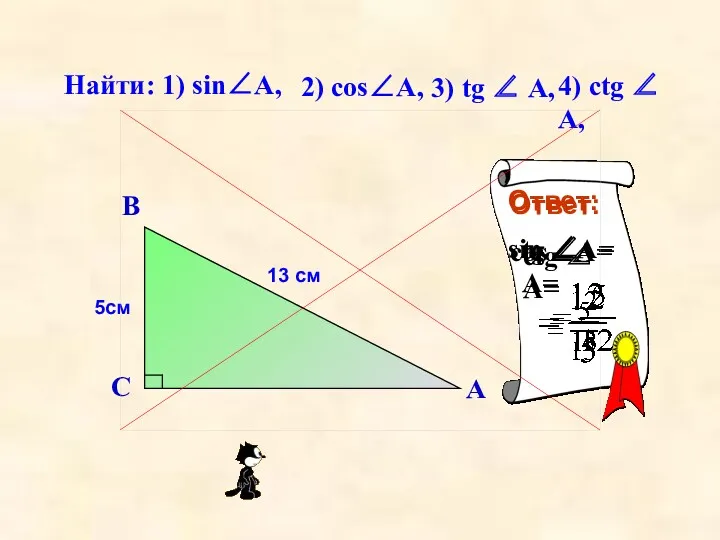 Значения синуса, косинуса, тангенса для углов 30, 45, 60 градусов
Значения синуса, косинуса, тангенса для углов 30, 45, 60 градусов Сфера. Шар. Части сферы и шара
Сфера. Шар. Части сферы и шара