Содержание
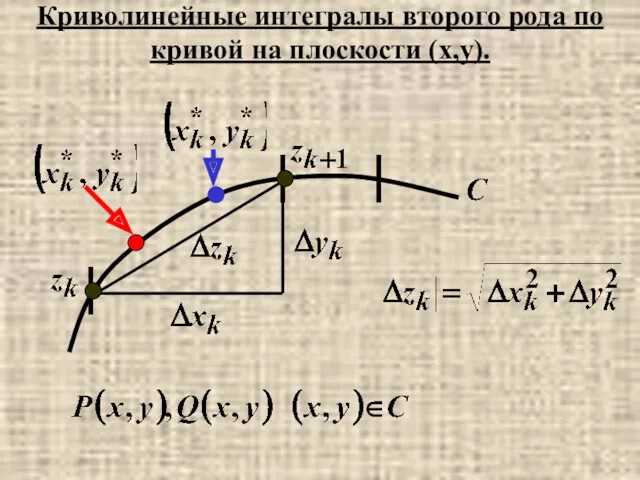
- 2. Криволинейные интегралы второго рода по кривой на плоскости (x,y).
- 3. Достаточные условия существования: кусочная гладкость кривой C; кусочная непрерывность и ограниченность функций P и Q.
- 4. Def. Интегралом от функции комплексной переменной f(z)=u(x,y)+iv(x,y) по кривой C комплексной плоскости z называется комплексное число
- 5. Замечания. Достаточные условие существования - кусочная гладкость контура C; - кусочная непрерывность и ограниченность u(x,y), v(x,y)
- 6. п.3. Свойства
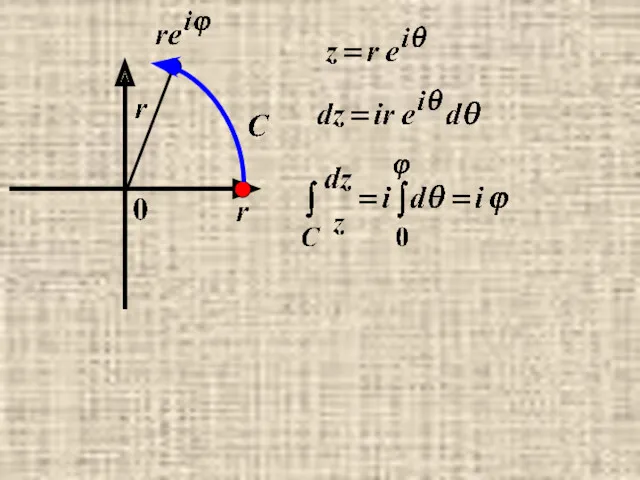
- 7. Пример.
- 8. 6) Замена переменной. Пусть ∃ однолистная
- 9. §6. Теорема Коши. п.1. Вспомогательные положения. Def. Область g⊂R2 называется квадрируемой если Def. Число называется площадью
- 10. Для функции f(x,y)∈C(g) и |f(x,y)|≤A в квадрируемой области g Def. Область g⊂R2 называется односвязной, если для
- 11. Пусть P(x,y), Q(x,y) ∈C(g), ∂g- кусочно- гладкий контур и Px, Py, Qx, Qy ⊂C(g), тогда Формула
- 12. п.2. Теорема 6.1 (Коши). в односвязной области g, то для ∀ замкнутого контура γ⊂g Если Доказательство.
- 13. ■
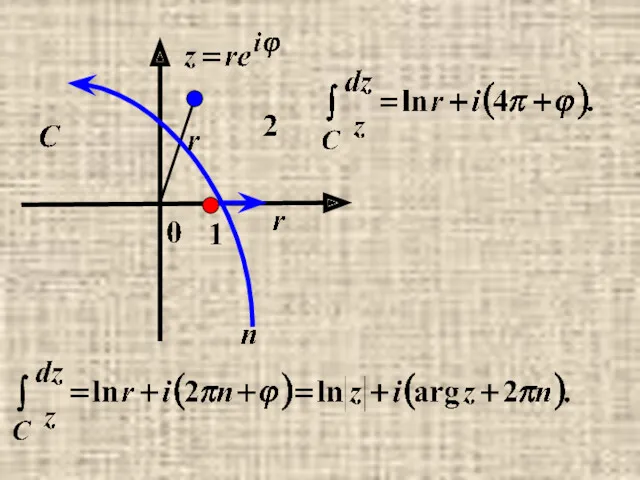
- 14. Замечания. 1) Односвязность области – важное требование! Пример.
- 15. Def. f(z) называется аналитической в замкнутой области g f(z)∈C∞(g), если f(z)∈C∞(g) и f(z) ∈C (g). Т.е.
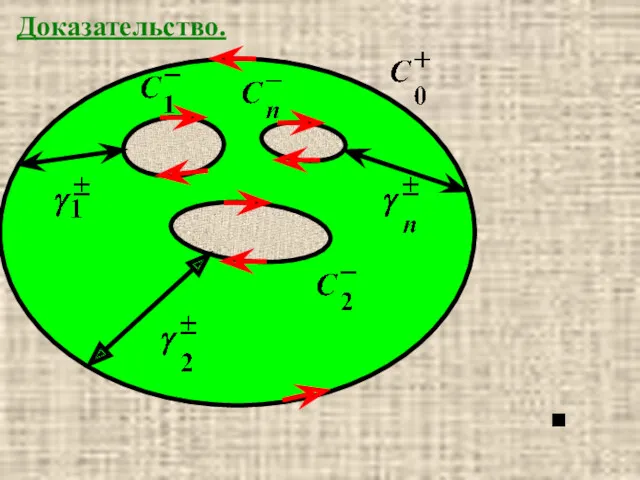
- 16. Теорема 6.3 (теорема Коши для многосвязной области). Пусть f(z)∈C∞ (g), g-многосвязная, ограниченная извне контуром C0, а
- 17. Доказательство. ■
- 18. п.3. Следствия теоремы Коши. 1) Если g- односвязная и f(z)∈C∞ (g), то для ∀z1, z2∈g При
- 19. 2) Неопределенный интеграл. Пусть g-односвязная область, f(z)∈C(g), для ∀ замкнутого контура γ⊂g неопределенный интеграл f(z).
- 20. Свойства неопределенного интеграла F(z). Теорема 6.4 Если g-односвязная область, для ∀ замкнутого контура γ⊂g f(z)∈C(g), то
- 21. Доказательство. ■
- 22. Понятие первообразной Def. Пусть f(z)∈C(g). Тогда первообразной F(z) функции f(z) в g называется ∀F(z)∈C∞ (g) такая,
- 23. Свойства неопределенного интеграла F(z). 1) Неопределенный интеграл F(z) в односвязной области g- первообразная для f(z). 2)
- 24. 4) Формула конечных приращений, вообще говоря не верна. 5) Формула Коши-Адамара.
- 26. 6) При вычислении интеграла от аналитической функции контур интегрирования можно деформировать так, чтобы он не выходил
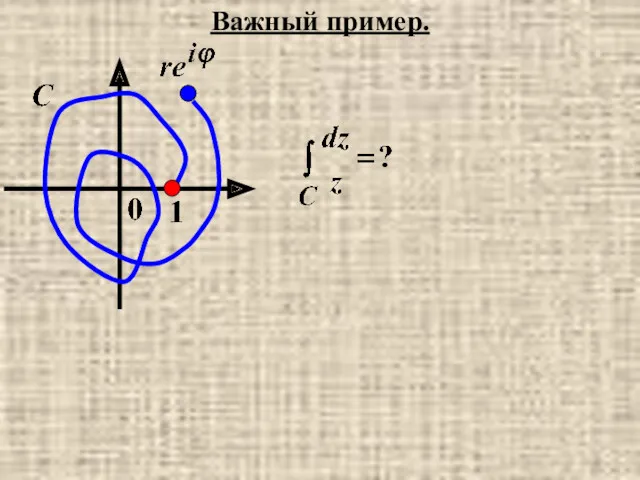
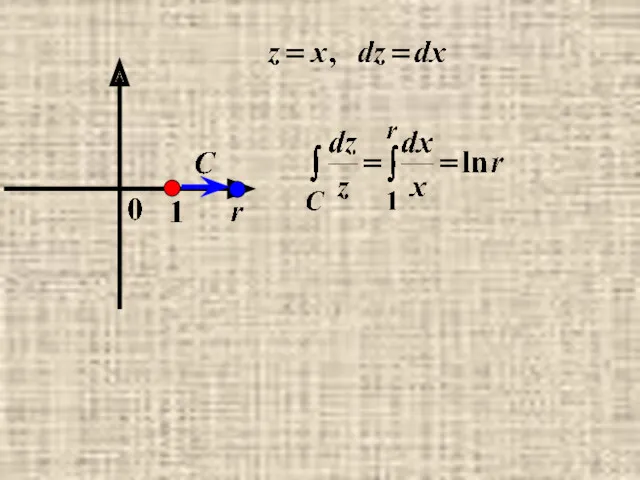
- 27. Важный пример.
- 32. Скачать презентацию



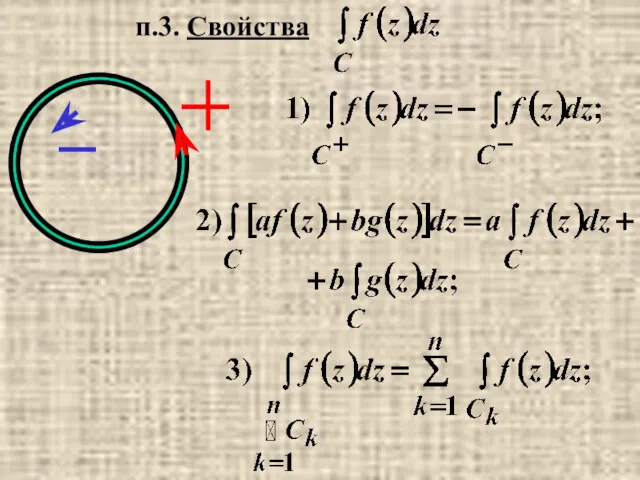
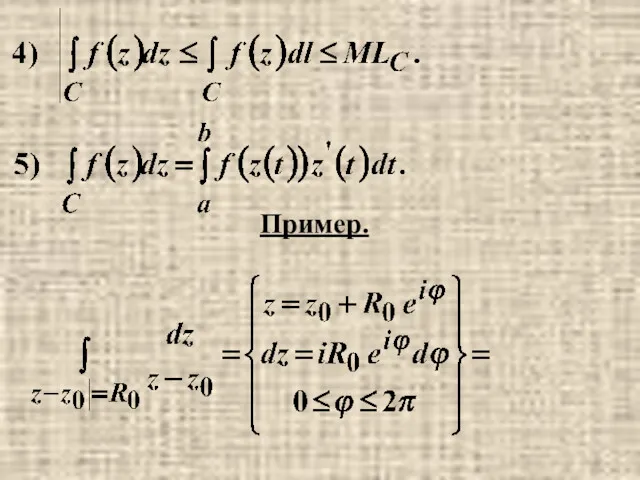
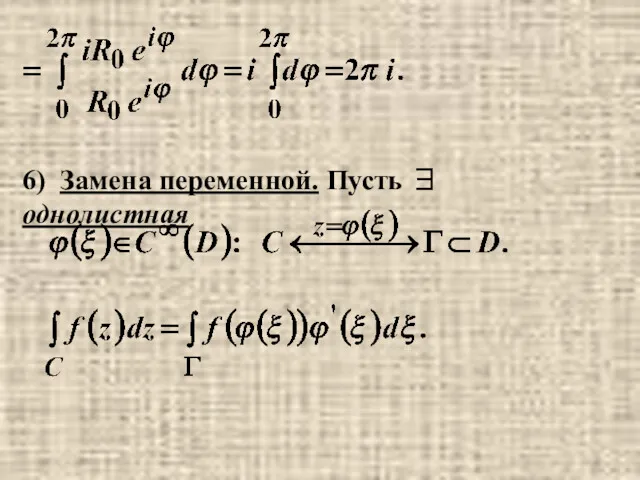




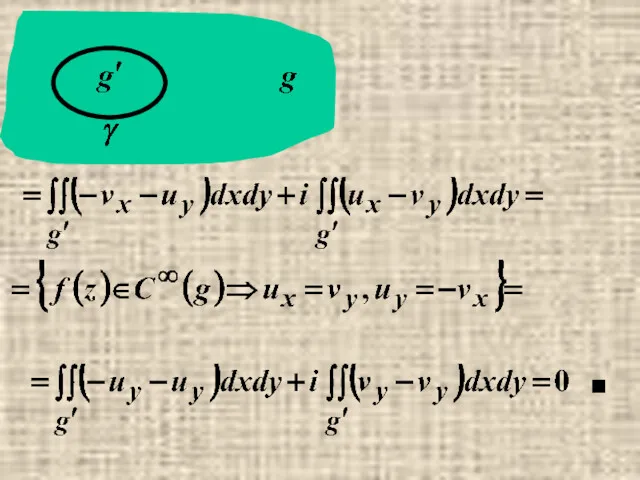












 В гости к царице Математике
В гости к царице Математике Умножение числа 2
Умножение числа 2 Сокращение алгебраических дробей
Сокращение алгебраических дробей Итоговый тест за курс начальной школы
Итоговый тест за курс начальной школы Полярные координаты. Параметрическая форма кривых
Полярные координаты. Параметрическая форма кривых Понятие отношения
Понятие отношения Доли. 3 класс.
Доли. 3 класс. Сложение вида …+2 , …+ 3. 1 класс
Сложение вида …+2 , …+ 3. 1 класс Периметр квадрата и прямоугольника. Презентация.
Периметр квадрата и прямоугольника. Презентация. Воображаемая геометрия Н.И. Лобачевского
Воображаемая геометрия Н.И. Лобачевского Презентация урока математики в 1 классе Из каких фигур состоит картинка
Презентация урока математики в 1 классе Из каких фигур состоит картинка Презентация Дроби. Нахождение части числа и нахождение числа по его части
Презентация Дроби. Нахождение части числа и нахождение числа по его части Степень с рациональным показателем и ее свойства
Степень с рациональным показателем и ее свойства Применение производной к исследованию функций. Схема исследования функции
Применение производной к исследованию функций. Схема исследования функции Урок математики Умножение и деление на 10 и на 100. Символы олимпиады Сочи 2014
Урок математики Умножение и деление на 10 и на 100. Символы олимпиады Сочи 2014 Составная задача на нахождение неизвестного уменьшаемого
Составная задача на нахождение неизвестного уменьшаемого Простейшие задачи в координатах
Простейшие задачи в координатах Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Сложение векторов. Правило треугольника
Сложение векторов. Правило треугольника Простейшие вероятностные задачи
Простейшие вероятностные задачи Внеклассное мероприятие по математике Своя игра
Внеклассное мероприятие по математике Своя игра Простые и составные числа
Простые и составные числа Додавання двоцифрових чисел. Ознайомлення із задачею на знаходження невідомого зменшуваного. Урок №124
Додавання двоцифрових чисел. Ознайомлення із задачею на знаходження невідомого зменшуваного. Урок №124 Решение уравнений
Решение уравнений Свойства прямоугольных треугольников. Задачи по готовым чертежам
Свойства прямоугольных треугольников. Задачи по готовым чертежам Обыкновенные дроби. Математика. 6 класс
Обыкновенные дроби. Математика. 6 класс Касательная к окружности. Решение задач на готовых чертежах
Касательная к окружности. Решение задач на готовых чертежах Давайте, посчитаем!
Давайте, посчитаем!