Содержание
- 2. План урока 1. Историческая справка 2. Определение иррационального уравнения 3. Уравнения, содержащие корень нечетной степени. 4.
- 3. Историческая справка Название «радикал» происходит от латинских слов radix – «корень», radicalis -- «коренной». Начиная с
- 4. Историческая справка (продолжение) В 1626г голландский математик А.Жирар ввел обозначение и т.д., которое стало быстро вытеснять
- 5. Иррациональные уравнения Иррациональным называется уравнение, в котором переменная входит под знаком корня (радикала). Например:
- 6. Уравнения, содержащие корень нечетной степени. Решая уравнения, содержащие корень нечетной степени, чтобы «избавиться от радикала», надо
- 7. Уравнения, содержащие корень нечетной степени (продолжение) х = 1, х = 2, х = 0 Решить
- 8. І. Уравнения вида В ОДЗ левая часть уравнения всегда неотрицательна – поэтому решение может существовать только
- 9. ПРИМЕРЫ 1) Решить уравнение Воспользуемся условием равносильности (*):
- 10. ПРИМЕРЫ 2) Решить уравнение Воспользуемся условием равносильности (*):
- 11. ІІ. Уравнения вида В ОДЗ обе части неотрицательны и при возведении в квадрат дает равносильное уравнение
- 12. ПРИМЕРЫ 1) Решить уравнение Воспользуемся условием равносильности (1): Ответ: х = 2,5
- 13. 2) Найдите произведение корней уравнения Воспользуемся условием равносильности (1): Ответ: Произведение корней равно - 2
- 14. ІІІ. Замена переменных. Решить уравнение 1. Пусть получим уравнение Значит решений нет. Ответ: х = 3.
- 15. Замена переменных Решить уравнение 2. Замена: , тогда , т.е. Обе части неотрицательны, возведём в квадрат
- 16. Решить самостоятельно уравнения 1. 2. 3. 4. 5. 6. 7. Ответы: - 1, 0, 2 2
- 17. Решить самостоятельно уравнения 8. 9. Замена : тогда Ответ : Замена : тогда Ответ:
- 18. Домножение на сопряженное выражение Решить уравнение ОДЗ: а) x = 0 - не является корнем иск.
- 20. Скачать презентацию

















 Математическая мозаика. Интеллектуальная игра
Математическая мозаика. Интеллектуальная игра Тренажер. Чтение графиков
Тренажер. Чтение графиков Делители. Наибольший общий делитель. Наименьшее общее кратное
Делители. Наибольший общий делитель. Наименьшее общее кратное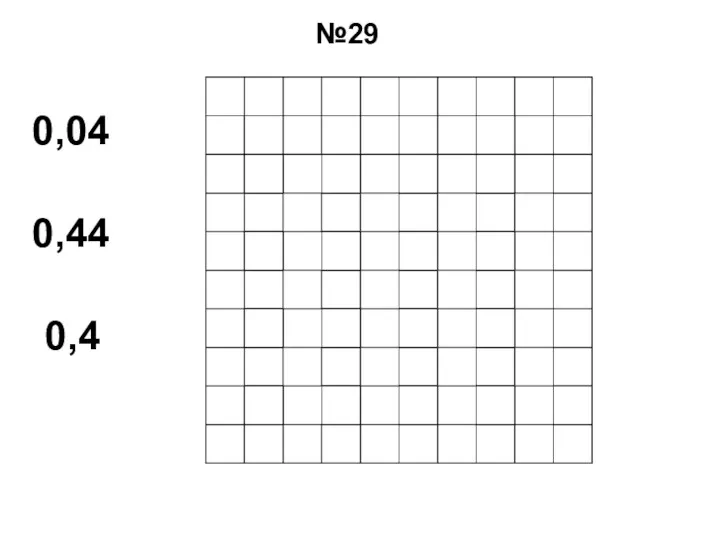 Действия с дробями
Действия с дробями Математическая модель
Математическая модель How many turkeys are there_- To Share
How many turkeys are there_- To Share Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике)
Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике) Основы геостатистики что такое геостатистика?
Основы геостатистики что такое геостатистика? Предмет эконометрики. Основные эконометрические модели
Предмет эконометрики. Основные эконометрические модели Полигон и гистограмма. Эмпирическая функция распределения
Полигон и гистограмма. Эмпирическая функция распределения Основы образования чертежа. Проецирование плоскости. Метрические задачи. (Лекция 2)
Основы образования чертежа. Проецирование плоскости. Метрические задачи. (Лекция 2) Больше, меньше или равно?
Больше, меньше или равно? Числовые выражения
Числовые выражения Кездейсоқ процесс – сигналдың моделі ретінде. Кездейсоқ процестердің ықтималдылық сипаттамалары
Кездейсоқ процесс – сигналдың моделі ретінде. Кездейсоқ процестердің ықтималдылық сипаттамалары Сокращение дробей
Сокращение дробей Функция y=k/x, её график и свойства
Функция y=k/x, её график и свойства Предмет, метод, задачи статистики, ее организация
Предмет, метод, задачи статистики, ее организация Число Пи
Число Пи Числовые неравенства и их свойства
Числовые неравенства и их свойства Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов История возникновения геометрии
История возникновения геометрии Преобразование графиков функций
Преобразование графиков функций Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера Математические диктанты
Математические диктанты 20231123_lineynaya_funktsiya_i_ee_grafik
20231123_lineynaya_funktsiya_i_ee_grafik Тест. Задания В3, ЕГЭ по математике
Тест. Задания В3, ЕГЭ по математике Умножение десятичных дробей. 6 класс
Умножение десятичных дробей. 6 класс Признаки параллельности прямых, 7 класс
Признаки параллельности прямых, 7 класс