Слайд 2

Приложения производной
Понятие производной имеет широкие приложения.
Важное приложение производной − задачи
на нахождение экстремальных (наибольших и наименьших) значений.
Оно основано на следующем факте, установленном Пьером Ферма:
если функция y=f(x) принимает в некоторой точке x = x0 экстремальное значение и существует производная в этой точке, то .
Слайд 3

Экстремумы функции, их необходимый и достаточный признаки
Точка экстремума функции – это
точка области определения функции, в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции.
Слайд 4

Критические точки
Значение аргумента х = х0, при котором производная обращается в
нуль или не существует, называется критическим.
Однако не во всякой критической точке функция имеет экстремум. Существует ряд достаточных условий наличия экстремума в точке х = х0. Сформулируем два из них.
Слайд 5

Первый достаточный признак существования экстремума
Если производная функции при переходе слева
направо через критическую точку х = х0 меняет знак с «−» на «+», то х = х0 − точка минимума, а при перемене знака с «+» на «−» х = х0 − точка максимума.
Слайд 6

Второй достаточный признак существования экстремума
Критическая точка x0 является точкой экстремума функции f(x), если
вторая производная функции в этой точке не равна нулю (f ''(x) ≠ 0); причём, если вторая производная больше нуля (f ''(x) > 0), то она является точкой максимума, а если вторая производная меньше нуля (f ''(x) < 0), то точкой минимума.
Слайд 7

Признаки возрастания и убывания функции
Теорема 1 (достаточный признак возрастания). Если во всех
точках некоторого промежутка производная функции больше нуля (f '(x) > 0), то функция f(x) возрастает в этом промежутке.
Теорема 2 (достаточный признак убывания). Если во всех точках некоторого промежутка производная функции меньше нуля (f '(x) < 0), то функция f(x) убывает на этом промежутке.
Слайд 8

Схема исследование функций и построения их графиков
Найти область определения функции D(f).
Установить четность и периодичность функции.
Установить поведение функции на концах промежутков области определения.
Найти промежутки возрастания и убывания функции, исследуя знак ее первой производной.
Найти точки экстремума (с помощью первой или второй производных, а также путем выявления точек, в которых функция не имеет производной или имеет бесконечную производную).
Слайд 9

Схема исследование функций и построения их графиков
Вычислить значения экстремумов (для чего
надо вычислить значения функции в точках экстремума).
Определить промежутки выпуклости и вогнутости графика функции (путем исследования знака второй производной: график функции выпуклый для тех значений х, при которых , и вогнутый, для тех х, при которых . Найти точки перегиба А(х0,f(х0)) – точки, при переходе через которые меняется направление выпуклости-вогнутости (при переходе через точку х0 вторая производная меняет знак). Более конкретно.
Слайд 10

Точки перегиба
Если в точке х0 функция f(x) имеет первую производную, а вторая производная в этой
точке равна нулю или не существует и, кроме того, при переходе через точку х0 меняет знак, то точка (х0, f(х0)) является точкой перегиба графика функции y = f(x).
Слайд 11

Схема исследование функций и построения их графиков
Найти вертикальные и наклонные асимптоты
графика функции. Асимптотами графика функции называются прямые, к которым при неограниченном удалении от начала координат ( ) приближается график функции, но их не пересекает.
Если функция не определена при х = а, то прямая х = а является вертикальной асимптотой.
Слайд 12

Схема исследование функций и построения их графиков
Для определения наклонной асимптоты y=kx+b
(в том числе и горизонтальной) при х→+∞ или х→-∞ числа k и b находят по формулам:
или
Найти точки пересечения графика функции с координатными осями.
Построить график функции.
Слайд 13

Пример
Исследовать функцию
и построить ее график.
Решение.
1. Данная функция определена на
всем множестве действительных чисел за исключением точки х = 0, таким образом, D(f) = (–∞, 0)∪(0, +∞).
2. Функция не является четной или нечетной, т. к.
Слайд 14

Пример
3. Установим, как ведет себя функция при х→+∞, х→-∞, х→0:
4. Находим
производную заданной функции:
Слайд 15

Пример
Производная обращается в нуль при х=6/5. Точка х=6/5 − критическая точка.
Производная не существует при х=0, однако, х=0 критической точкой не является, т. к. не принадлежит области определения.
На промежутке х∈(0; 6/5) производная данной функции положительна, значит, функция на этом промежутке возрастает.
При х∈(-∞; 0)∪(6/5; +∞) производная отрицательна, следовательно, при этих значениях х функция убывает.
Слайд 16

Пример
5. Точка х=6/5 – точка максимума, так как при переходе слева
направо через нее производная меняет знак с «+» на «–».
6. Максимальное значение функции равно:
7. Находим вторую производную данной функции:
Слайд 17

Пример
Вторая производная при х∈(-∞; 0)∪(0; 1,8) отрицательна, следовательно график функции будет
выпуклым на этом промежутке.
При х∈(1,8; +∞) график функции будет во-гнутым, т. к. на этом промежутке вторая производная положительна.
В точке с абсциссой х=1,8 график заданной функции имеет перегиб. Найдем значение функции при х=1,8; получим:
Точка перегиба имеет координаты (1,8; 3,85).
Слайд 18

Пример
8. При х = 0 функция не определена. Таким образом, прямая
х = 0 является для графика вертикальной асимптотой.
Уравнение наклонной асимптоты будем искать в виде y=kx+b.
Слайд 19

Пример
Таким образом, при х→+∞ наклонной асимптотой будет прямая у = 2
(уравнение горизонтальной прямой).
Несложно установить, что эта же прямая будет асимптотой и при х→-∞.
График функции не пересекает ось Оу. Точки пересечения графика с осью Ох находим, решая уравнение:
Получаем х1 = -3; х2 = 0,5.


















 Задачи на противоположное движение урок+презентация для 4 класса
Задачи на противоположное движение урок+презентация для 4 класса Тест по теме: Призма. Часть 1
Тест по теме: Призма. Часть 1 Презентация к уроку по математике (старшая группа) по теме: Методический театр- сказка.
Презентация к уроку по математике (старшая группа) по теме: Методический театр- сказка.  Подготовка к итоговой работе по математике. 4 класс
Подготовка к итоговой работе по математике. 4 класс Математическое кафе Апельсин
Математическое кафе Апельсин Решение примеров и задач на умножение и деление чисел 0 и1
Решение примеров и задач на умножение и деление чисел 0 и1 Презентация по математике по теме Задачи на движение4 класс
Презентация по математике по теме Задачи на движение4 класс Площадь и периметр прямоугольника
Площадь и периметр прямоугольника Векторы в пространстве. Координаты вектора
Векторы в пространстве. Координаты вектора Сложение чисел с разными знаками
Сложение чисел с разными знаками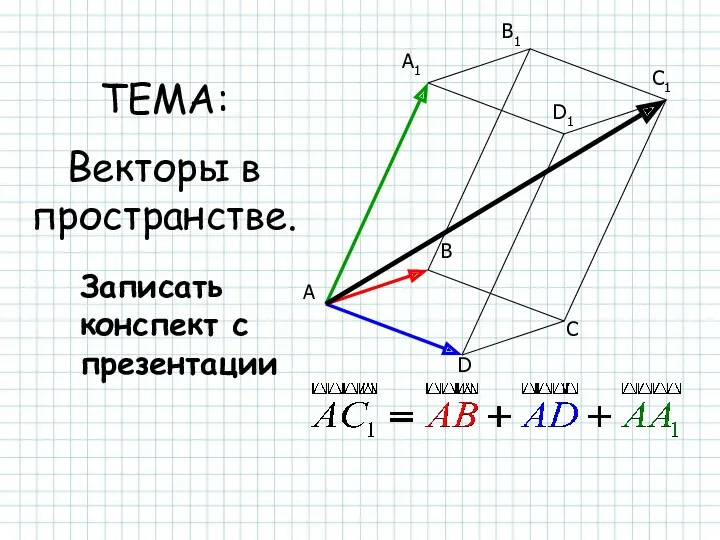 Векторы в пространстве
Векторы в пространстве Ломаная
Ломаная Олимпиады для начальной школы (3-4 класс).
Олимпиады для начальной школы (3-4 класс). Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Сложение и вычитание дробей. Проверочная работа
Сложение и вычитание дробей. Проверочная работа Десятичное приближение обыкновенной дроби
Десятичное приближение обыкновенной дроби Игра Экология и математика
Игра Экология и математика Четырёхугольники
Четырёхугольники Чертежи и развертки простых геометрических тел
Чертежи и развертки простых геометрических тел Геометрические фигуры. Треугольник
Геометрические фигуры. Треугольник Умножение десятичных дробей
Умножение десятичных дробей Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Великие математики древности
Великие математики древности Вертикальные углы
Вертикальные углы Решение задач наприменение аксиом стереометрии и их следствий
Решение задач наприменение аксиом стереометрии и их следствий Статистика. Загальні поняття про статистику
Статистика. Загальні поняття про статистику Умножение и деление на 5
Умножение и деление на 5 Основные понятия комбинаторики: размещения, сочетания, перестановки и формулы для их вычисления
Основные понятия комбинаторики: размещения, сочетания, перестановки и формулы для их вычисления