Содержание
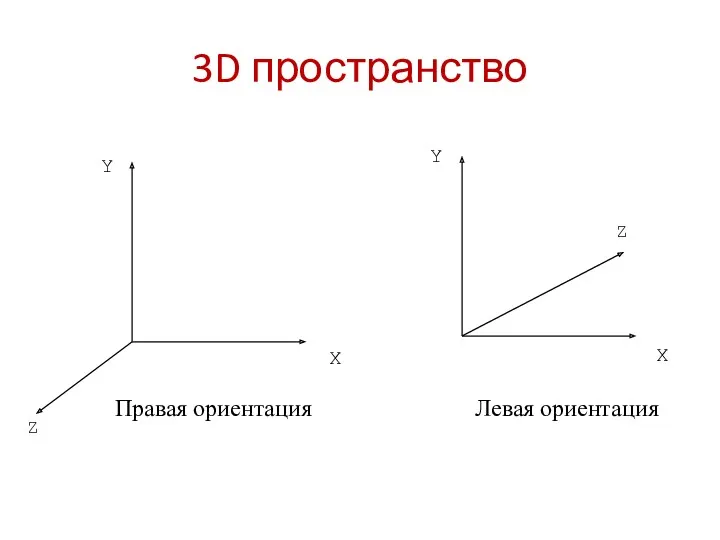
- 2. 3D пространство Y Z X Y Z X Правая ориентация Левая ориентация
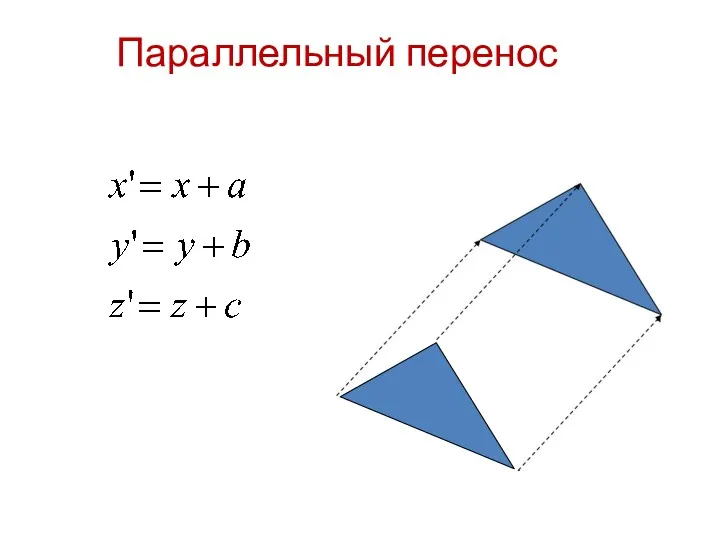
- 3. Параллельный перенос
- 4. Параллельный перенос
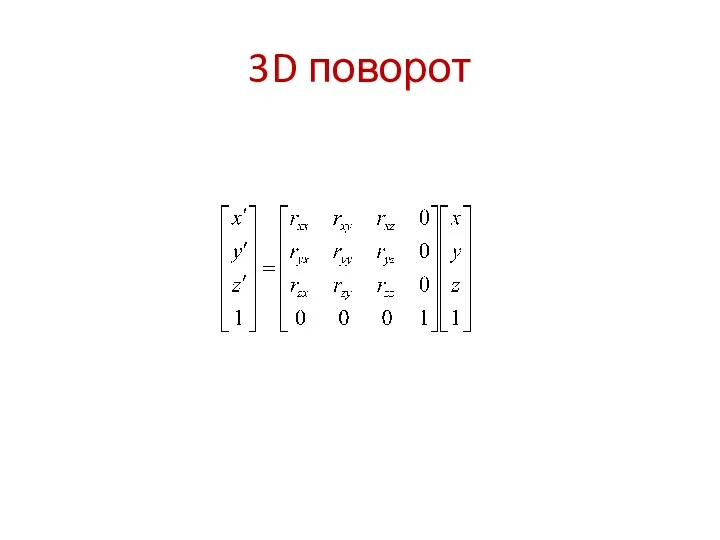
- 5. 3D поворот Рассматривается поворот осей координат вокруг начала координат. В матричном представлении: всякая ортогональная 3х3 матрица
- 6. 3D поворот
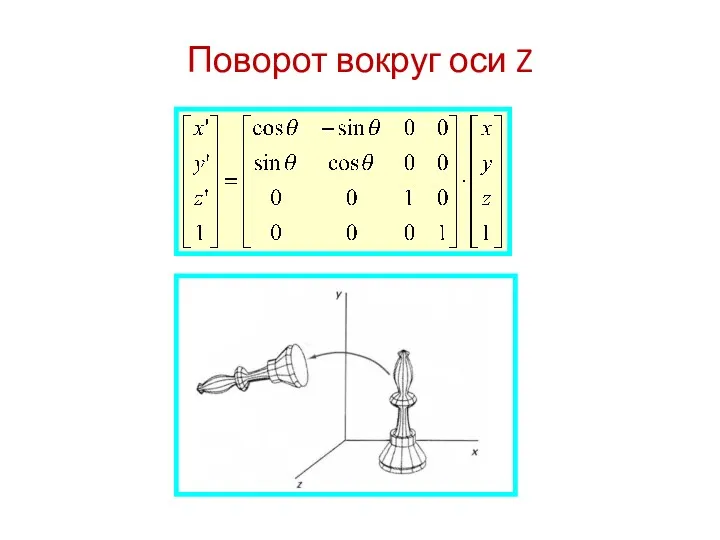
- 7. Поворот вокруг оси Z
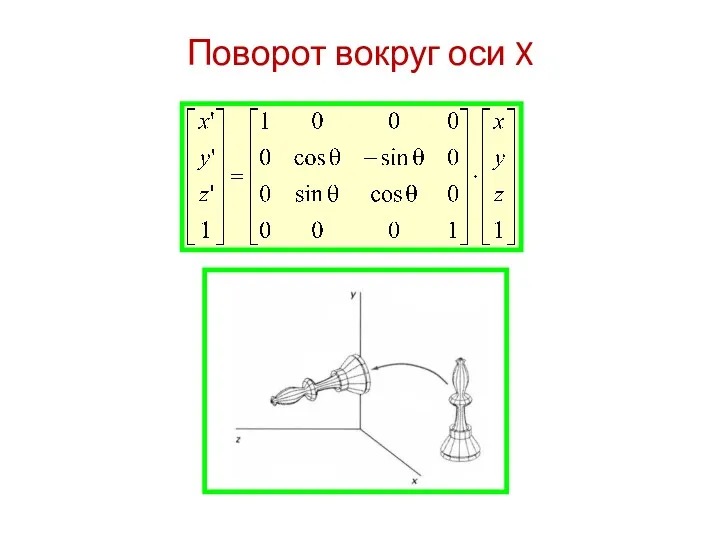
- 8. Поворот вокруг оси X
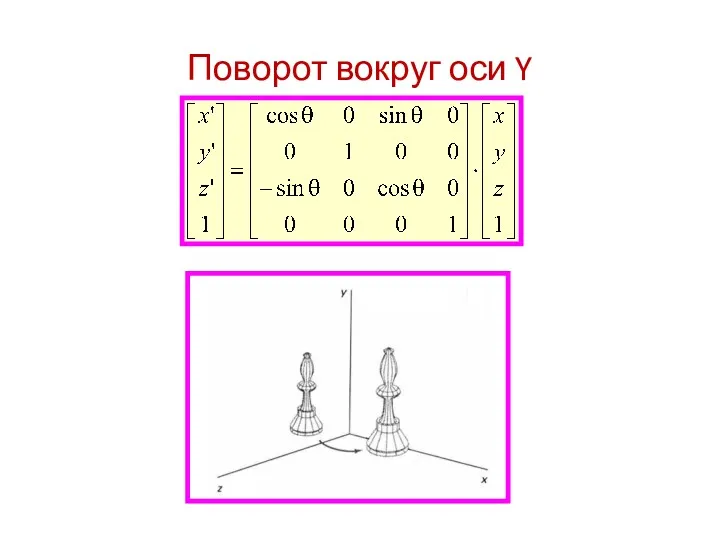
- 9. Поворот вокруг оси Y
- 10. Уравнение поверхности 2-го порядка Уравнение поверхности 2-го порядка главная(квадратичная) часть линейная часть . Основная задача состоит
- 11. Составим матрицу Так как матрица симметрическая, то существует ортогональное преобразование (поворот), приводящее главную часть к главным
- 12. 1. Все собственные числа отличны от нуля. Выделим полные квадраты выполним параллельный перенос получим
- 13. 1. Все собственные числа отличны от нуля. 1.1. Если знаки одинаковы и с=0, преобразуем уравнение Получим
- 14. 1. Все собственные числа отличны от нуля. 1.2. Если знаки и с одинаковы, то действительных решений
- 15. 1. Все собственные числа отличны от нуля. 1.3. Если знаки , с одной стороны, и с
- 16. Эллипсоид Каноническое уравнение трехосного эллипсоида имеет вид a b c полуоси эллипсоида. Центр этого эллипсоида находится
- 17. 1. Все собственные числа отличны от нуля. 1.4. Знаки различны, пусть знаки отличаются от знака и
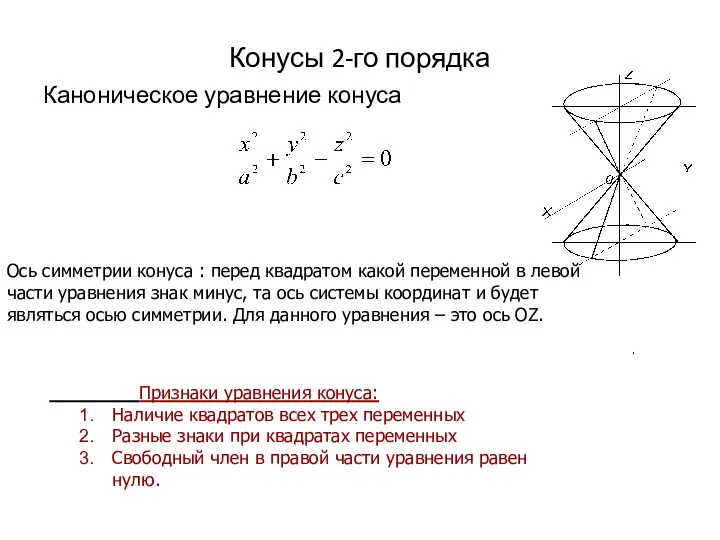
- 18. Конусы 2-го порядка Каноническое уравнение конуса Признаки уравнения конуса: Наличие квадратов всех трех переменных Разные знаки
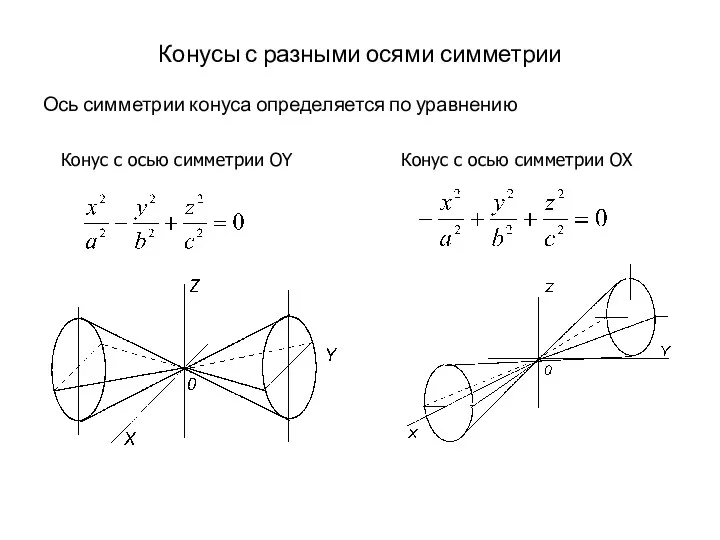
- 19. Конусы с разными осями симметрии Ось симметрии конуса определяется по уравнению Конус с осью симметрии OY
- 20. 1. Все собственные числа отличны от нуля. 1.5. Знаки различны, пусть знаки отличаются от знака и
- 21. Гиперболоиды Канонические уравнения гиперболоидов Каноническое уравнение однополостного гиперболоида Признаки уравнения однополостного гиперболоида: Наличие квадратов всех трех
- 22. Разные ориентации однополостных гиперболоидов Ориентация гиперболоида зависит от того, перед какой переменной в каноническом уравнении стоит
- 23. Гиперболоиды Каноническое уравнение двуполостного гиперболоида Признаки уравнения двуполостного гиперболоида: Наличие квадратов всех трех переменных Разные знаки
- 24. Разные ориентации двуполостного гиперболоида Каноническое уравнение двуполостного гиперболоида содержит два знака минус в уравнении. Один знак
- 25. 2. Одно из собственных чисел равно нулю ( ). Выделим полные квадраты 2.1. , выполним параллельный
- 26. 2. Одно из собственных чисел равно нулю ( ). 2.1.1. с=0, знаки одинаковы. Получим уравнение плоскости
- 27. 2. Одно из собственных чисел равно нулю ( ). 2.1.3. , знаки одинаковы и отличаются от
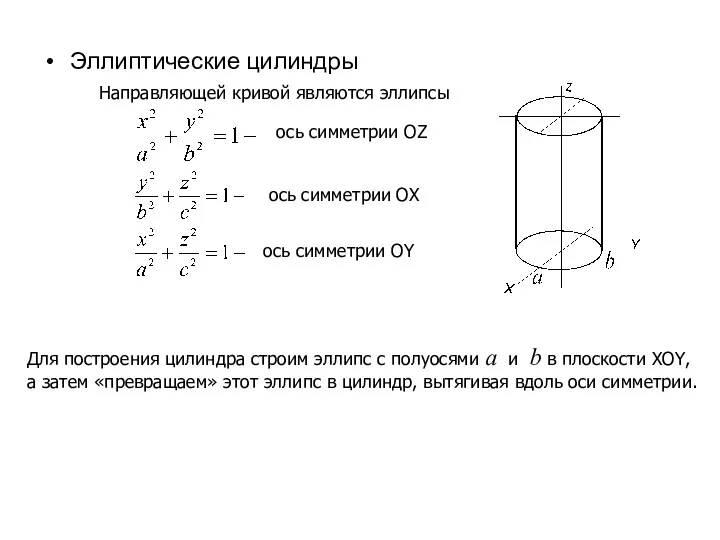
- 28. Эллиптические цилиндры ось симметрии OZ ось симметрии OX ось симметрии OY Для построения цилиндра строим эллипс
- 29. 2. Одно из собственных чисел равно нулю ( ). 2.1.4. с=0, знаки различны. Получим уравнение плоскостей
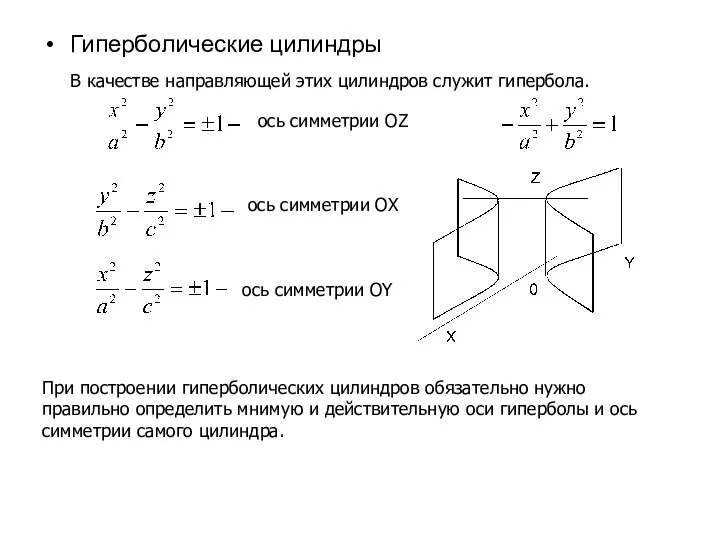
- 30. Гиперболические цилиндры ось симметрии OZ ось симметрии OX ось симметрии OY При построении гиперболических цилиндров обязательно
- 31. 2. Одно из собственных чисел равно нулю ( ). 2.2. Выделим полные квадраты выполним параллельный перенос
- 32. 2. Одно из собственных чисел равно нулю ( ). Преобразуем Получим каноническое уравнение параболоида
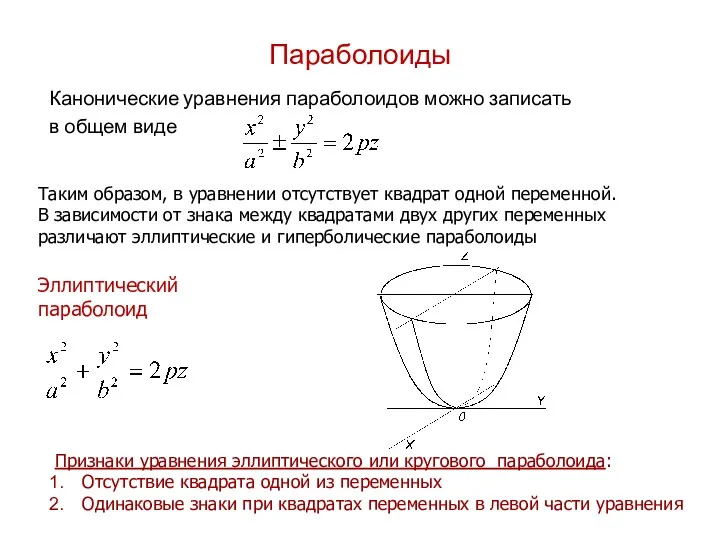
- 33. Параболоиды Канонические уравнения параболоидов можно записать в общем виде Таким образом, в уравнении отсутствует квадрат одной
- 34. Гиперболический параболоид Каноническое уравнение гиперболического параболоида имеет вид Признаки уравнения гиперболического параболоида: Отсутствие квадрата одной из
- 35. 3. Два собственных числа равны нулю ( ). Выделим полный квадрат выполним параллельный перенос Получим
- 36. 3. Два собственных числа равны нулю ( ). 3.1. , получим Это есть либо уравнения пересекающихся
- 37. 3. Два собственных числа равны нулю ( ). 3.2. хотя бы один из : перенос: поворот:
- 39. Скачать презентацию

























 Методическая разработка внеклассного мероприятия по математике 1 класс
Методическая разработка внеклассного мероприятия по математике 1 класс Элективный курс по математике Практикум по решению задач
Элективный курс по математике Практикум по решению задач Развёртки поверхностей. Аксонометрические проекции
Развёртки поверхностей. Аксонометрические проекции Тренажер по математике Сложение и вычитание однозначных чисел
Тренажер по математике Сложение и вычитание однозначных чисел Прямокутна система координат. 6 клас
Прямокутна система координат. 6 клас Правильные многоугольники
Правильные многоугольники Розв'язування задач за допомогою рівнянь
Розв'язування задач за допомогою рівнянь Золотое сечение
Золотое сечение Прогрессии. Арифметическая прогрессия
Прогрессии. Арифметическая прогрессия Формирование познавательных ууд на уроках математики в начальной школе.
Формирование познавательных ууд на уроках математики в начальной школе. Правильные многоугольники
Правильные многоугольники Электронно-демонстрационная игра
Электронно-демонстрационная игра Медицинская статистика. Значение, методы
Медицинская статистика. Значение, методы Статистические методы обработки экспериментальных данных
Статистические методы обработки экспериментальных данных Транспортная задача. Метод потенциалов
Транспортная задача. Метод потенциалов Подготовка к ЕГЭ (профильный уровень). Задание 6. Математика
Подготовка к ЕГЭ (профильный уровень). Задание 6. Математика Деление вида 63 : 3
Деление вида 63 : 3 Площадь прямоугольника
Площадь прямоугольника Таблица сложения
Таблица сложения Сравнение десятичных дробей
Сравнение десятичных дробей Свойства тригонометрических функций
Свойства тригонометрических функций Параллелограмм (8 класс)
Параллелограмм (8 класс) Таблица умножения на 2. Тренажёр-раскраска
Таблица умножения на 2. Тренажёр-раскраска Деление многозначных чисел и решение задач на движение
Деление многозначных чисел и решение задач на движение Дидактическая игра по сенсорному развитию у дошкольников ЗАСЕЛИ ДОМИКИ
Дидактическая игра по сенсорному развитию у дошкольников ЗАСЕЛИ ДОМИКИ Вычисление площадей фигур на клетчатой бумаге. Формула Пика (8 класс)
Вычисление площадей фигур на клетчатой бумаге. Формула Пика (8 класс) Построение таблиц истинности сложных высказываний
Построение таблиц истинности сложных высказываний Равнобедренный треугольник. Геометрия 7 класс
Равнобедренный треугольник. Геометрия 7 класс