Содержание
- 2. Измерение – это приписывание объекту числа по определенному правилу. Это правило устанавливает соответствие между измеряемым свойством
- 3. Измерительные шкалы (С. Стивенс, 1951 год) Неметрические: Номинативная шкала (шкала наименований) Ранговая (порядковая) шкала Метрические: Интервальная
- 4. Номинативная шкала (шкала наименований) Неметрическая. Измерение состоит в присвоении признаку определенного обозначения или символа. Процедура измерения
- 5. Ранговая (порядковая) шкала Неметрическая. Измерение предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства.
- 6. Интервальная шкала Метрическая Измерение отражает не только различия в уровне выраженности признака, но и то, на
- 7. Абсолютная шкала (шкала отношений) Метрическая Установлена нулевая точка, соответствующая полному отсутствию выраженности измеряемого признака. В силу
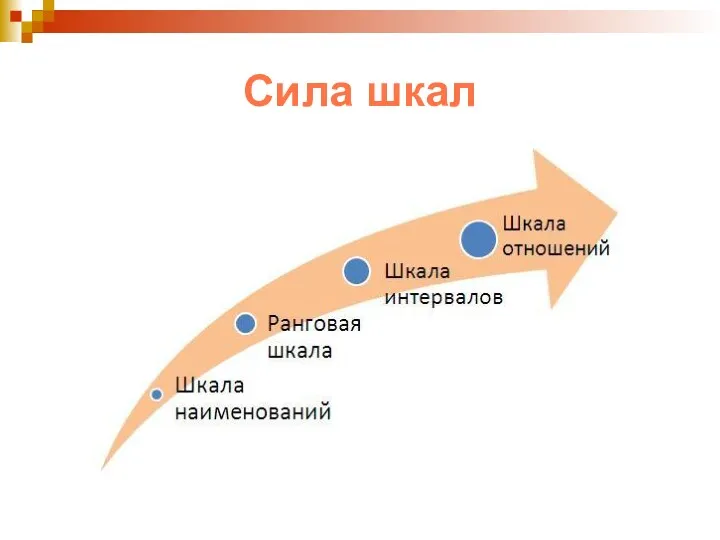
- 8. Сила шкал
- 9. Типы данных (применительно к статистической обработке) Качественные Номинативные Ранговые (порядковые, полуколичественные) Количественные Дискретные Непрерывные
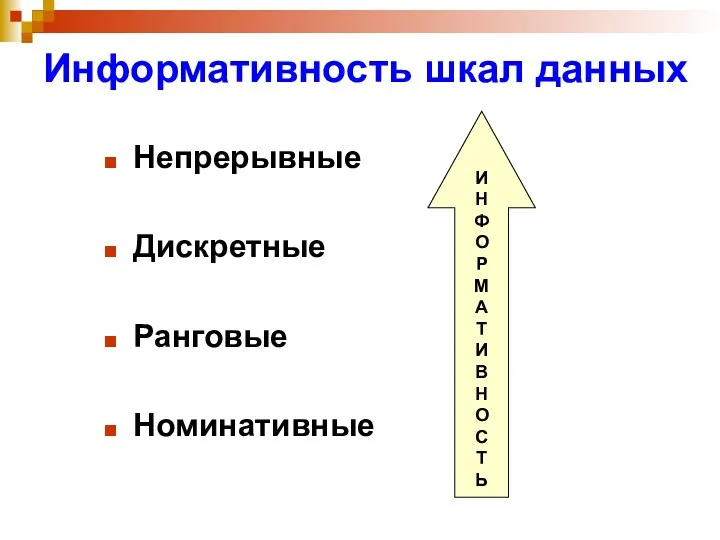
- 10. Информативность шкал данных Непрерывные Дискретные Ранговые Номинативные И Н Ф О Р М А Т И
- 11. Преобразование данных количественные ? ранговые ? номинативные
- 12. Описательная статистика
- 13. Генеральная совокупность Всё множество объектов, обладающее изучаемым признаком.
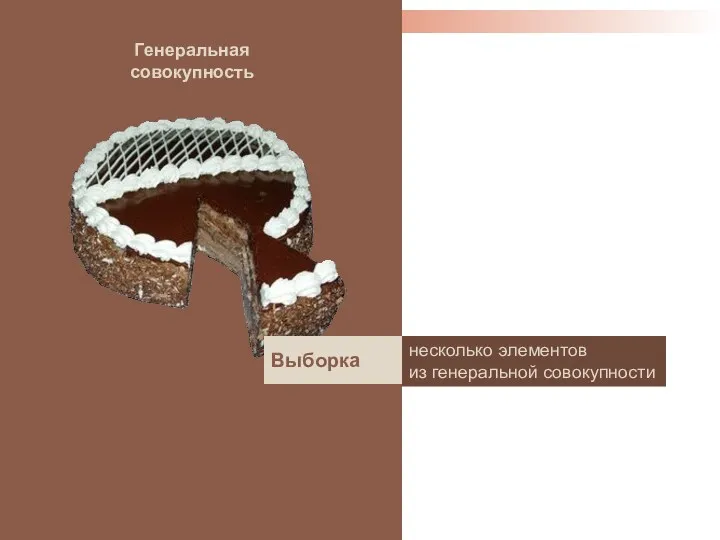
- 14. Генеральная совокупность несколько элементов из генеральной совокупности Выборка
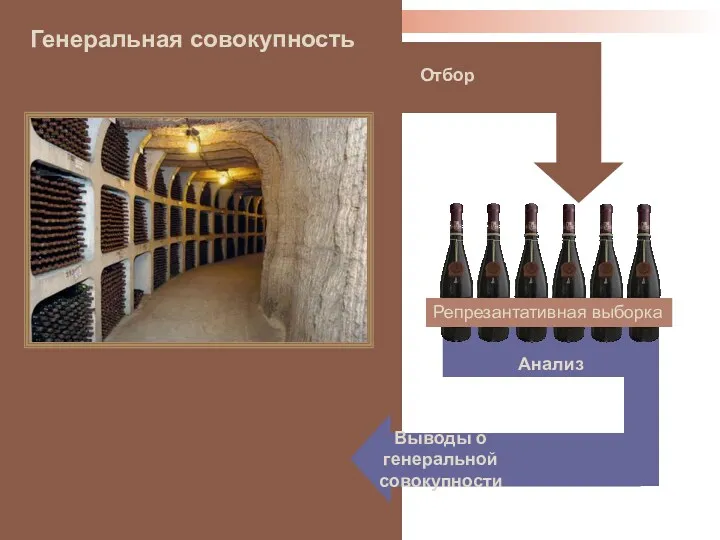
- 15. Генеральная совокупность Анализ Выводы о генеральной совокупности Отбор Репрезантативная выборка
- 16. Характеристики, которые базируются на данных массовых наблюдений, называют обобщающими показателями или числовыми характеристиками. Эти показатели характеризуют
- 17. Описательная статистика нужна для: «Сжатия» и концентрирования информации Первичного анализа полученной информации Представления и сравнения результатов
- 18. Ценность описательной статистики в том, что она дает сжатую и концентрированную характеристику изучаемого явления. Например: На
- 19. Что характеризует? Центр распределения Разброс значений Форму кривой
- 20. §1. Меры центральной тенденции
- 21. Важнейшие среди обобщающих показателей - средние величины, т. е. такие значения признака, вокруг которых группируются отдельные
- 22. В зависимости от характера задачи пользуются тем или иным видом средней величины. К ним принадлежат среднее
- 23. Выборочная средняя – это средняя арифметическая всех вариант в выборке. Обозначается Вычисляется по формуле: (для группированной
- 24. 1.1. Среднее арифметическое (выборочная средняя) Сущность среднего арифметического состоит в следующем: если каждое наблюдение заменить средним,
- 25. 1.1. Среднее арифметическое (выборочная средняя) Еще одно свойство выборочной средней состоит в том, что сумма расстояний
- 26. 1.1. Среднее арифметическое (выборочная средняя) Например: Рассмотрим среднюю месячную зарплату работников некоторого предприятия. Пусть, например, в
- 27. 1.2. Медиана Медиана (обозначается Мd или Ме) — это значение, которое делит упорядоченное множество данных пополам,
- 28. 1.2. Медиана Если объем совокупности нечетный и равен 2n + 1, и варианты размещены в порядке
- 29. 1.2. Медиана Если количество элементов четное и равно 2n, то нет варианты, которая бы делила совокупность
- 30. 1.2. Медиана Ранее рассматривался пример с зарплатой работников некоторой фирмы, в которой работает 20 человек, зарплата
- 31. 1.2. Медиана Вычисление медианы имеет следующие преимущества: она мало чувствительна к выбросам ее возможно вычислять не
- 32. 1.3. Мода Мода - это такое значение признака, которое встречается наиболее часто. В случае дискретных рядов
- 33. 1.3. Мода Когда два соседних значения имеют одинаковые частоты и они больше частоты любого другого значения,
- 34. 1.4. Ограничения при работе с мерами центральной тенденции Следует всегда помнить, что меры центральной тенденции отражают
- 35. 1.5. Ограничения при работе с мерами центральной тенденции Выбирая меру центральной тенденции, нужно руководствоваться знанием ее
- 36. Однажды пятеро мужчин сидели рядом на скамейке парка. Двое были бродягами, имущество которых выражалось в 25
- 37. Мода – 25 центов. Медиана – 2 000 долларов. Среднее – 1 003 400,10 долларов.
- 38. §2. Меры изменчивости
- 39. Чтобы определить, насколько хорошо та или иная мера центральной тенденции выражает «типичного» представителя совокупности, следует воспользоваться
- 40. 2.1. Размах Размах просто измеряет на числовой шкале расстояние, в пределах которого изменяются оценки. Поскольку существуют
- 41. 2.1. Размах Исключающий размах — это разность максимального и минимального значений в выборке. Например: исключающий размах
- 42. 2.1. Размах Включающий размах — это разность между естественной верхней границей интервала, содержащего максимальное значение, и
- 43. 2.2. Квартильный размах Кванти́ль в математической статистике - такое число, что заданная случайная величина не превышает
- 44. 2.2. Квартильный размах Квартильный размах – это интервал, в котором вокруг медианы сосредоточилось 50% значений. Он
- 45. 2.3. Дисперсия Размах представляет собой меру рассеяния, разброса, неоднородности или изменчивости. Эта величина возрастает с ростом
- 46. Выборочная дисперсия – это средняя арифметическая квадратов отклонений вариант от выборочной средней Обозначается DB Вычисляется по
- 47. 2.3. Дисперсия Исправленная выборочная дисперсия: Чаще всего вычисляют сразу исправленную дисперсию по формуле:
- 48. 2.3. Дисперсия Ценность дисперсии заключается в том, что, являясь мерой варьирования числовых значений признака вокруг его
- 49. 2.4. Среднеквадратическое и стандартное отклонение Мерой изменчивости, тесно связанной с дисперсией, является стандартное отклонение. Среднеквадратическое (стандартное
- 50. 2.5. Коэффициент вариации Cv Дисперсия и среднее отклонение применимы и для сравнительной оценки одноимённых средних величин.
- 51. 2.5. Коэффициент вариации Cv Одним из относительных показателей вариации является коэффициент вариации. Этот показатель представляет собой
- 52. 2.5. Коэффициент вариации Cv Различные признаки характеризуются различными коэффициентами вариации. Но в отношении одного и того
- 53. §3. Показатели формы кривой распределения
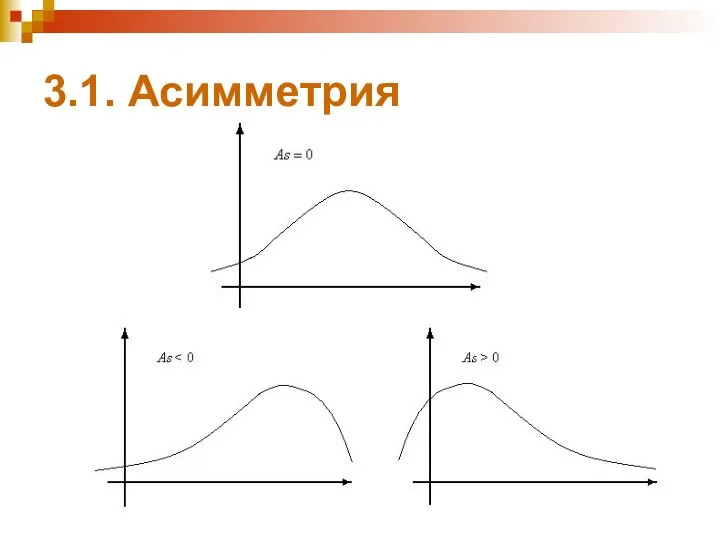
- 54. 3.1. Асимметрия Одно из наиболее важных свойств распределения частот – степень асимметрии. Практически точно симметричные полигоны
- 55. 3.1. Асимметрия
- 56. 3.2. Эксцесс Cтатистики описывают три свойства или особенности выборок: центральную тенденцию изменчивость симметрию Четвертое свойство завершает
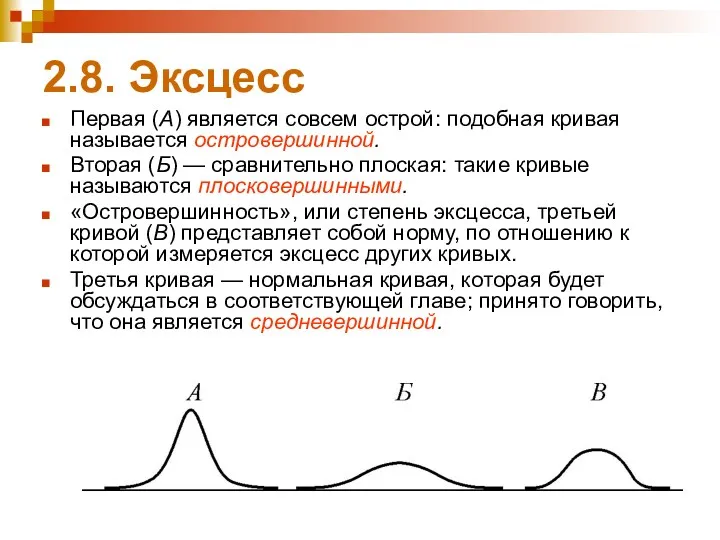
- 57. 2.8. Эксцесс Первая (А) является совсем острой: подобная кривая называется островершинной. Вторая (Б) — сравнительно плоская:
- 58. 2.8. Эксцесс Понятие «эксцесс» применимо лишь к унимодальным распределениям и относится к крутизне кривой в окрестности
- 60. Скачать презентацию



















































 Игра Я знаю всё
Игра Я знаю всё Деловая игра как форма знакомства с профессиями на уроках математики
Деловая игра как форма знакомства с профессиями на уроках математики Сравнение чисел. 6 класс
Сравнение чисел. 6 класс Степень числа. Квадрат и куб числа. 5 класс
Степень числа. Квадрат и куб числа. 5 класс Действия с обыкновенными дробями. Создание ОАО
Действия с обыкновенными дробями. Создание ОАО Десятичные дроби. Повторение
Десятичные дроби. Повторение Математический кубик-рубик. Натуральные числа
Математический кубик-рубик. Натуральные числа Умножение многочлена на многочлен
Умножение многочлена на многочлен Урок математики в 1 классе Табличное вычитание ОС Школа 2100
Урок математики в 1 классе Табличное вычитание ОС Школа 2100 proizvodnaya-slozhnoy-funkcii
proizvodnaya-slozhnoy-funkcii Целеполагание как этап современного урока в условиях ФГОС
Целеполагание как этап современного урока в условиях ФГОС Признаки равенства треугольников. Задачи на готовых чертежах
Признаки равенства треугольников. Задачи на готовых чертежах Многоугольники. Четырехугольники
Многоугольники. Четырехугольники Модуль числа
Модуль числа Розв’язування логарифмічних рівнянь
Розв’язування логарифмічних рівнянь Моделирование методом Монте-Карло
Моделирование методом Монте-Карло Урок математики по УМК Перспективная начальная школа 2 класс,четвёртая четверть. Урок-путешествие в королевство Задачи Диск
Урок математики по УМК Перспективная начальная школа 2 класс,четвёртая четверть. Урок-путешествие в королевство Задачи Диск Числовые и буквенные выражения
Числовые и буквенные выражения Графы. Решение задач
Графы. Решение задач Изображение трехмерных объектов
Изображение трехмерных объектов Подготовка к контрольной работе по теме Треугольники
Подготовка к контрольной работе по теме Треугольники Симметрия на плоскости
Симметрия на плоскости Презентация Занимательный материал в обучении дошкольников элементарной математике
Презентация Занимательный материал в обучении дошкольников элементарной математике Математические методы в историческом исследовании. (Лекция 1)
Математические методы в историческом исследовании. (Лекция 1) Взаимно обратные числа. Деление
Взаимно обратные числа. Деление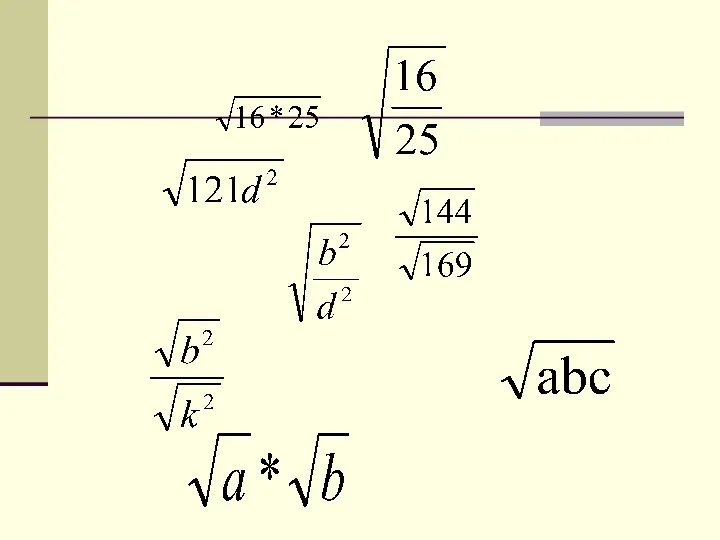 Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Педагогические условия повышения уровня подготовки учащихся к ОГЭ по математике
Педагогические условия повышения уровня подготовки учащихся к ОГЭ по математике Часы
Часы