Слайд 2

Основные понятия
Комплексным числом называется выражение вида
где и – действительные числа,
а
– мнимая единица.
Слайд 3

Два комплексных числа
называются равными тогда и только тогда, когда
Комплексное
число
равно 0 тогда и только тогда, когда
Слайд 4

Понятия «больше» и «меньше» для комплексных чисел не определяются.
Два комплексных числа
называются сопряженными.
Справедливо равенство
Слайд 5

Извлечение корней из комплексных чисел
Корнем n-ой степени из комплексного числа называется
комплексное число ,
удовлетворяющее равенству
Т.е. , если
Слайд 6

Пример
Вычислить
Решить уравнение
Решить уравнение
Решение. 1.
Слайд 7
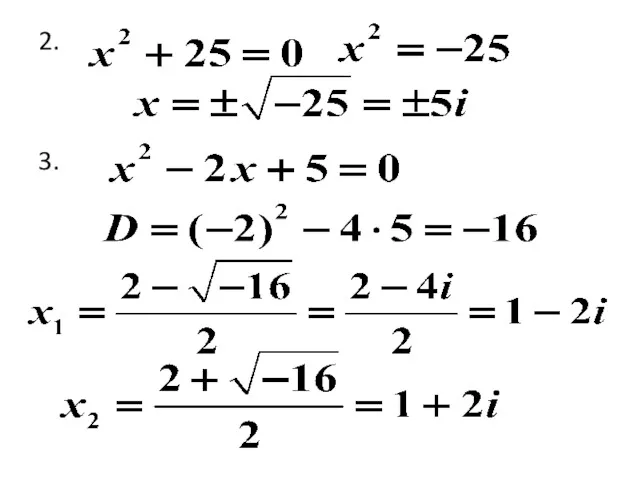
Слайд 8

Тема: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§1. Дифференциальные уравнения первого порядка
Слайд 9

Дифференциальные уравнения первого порядка
Уравнение
связывающее независимую переменную x, искомую функцию
y и ее производную y’, называется
дифференциальным уравнением первого порядка
(ДУ первого порядка).
Слайд 10

Если дифференциальное уравнение можно записать в виде
то говорят, что оно разрешимо
относительно производной.
Это уравнение можно записать в виде
так как
или, в более общем виде
Слайд 11

Решение дифференциального уравнения
Решением (или интегралом) дифференциального уравнения первого порядка называется
любая функция , которая при подстановке в уравнение обращает его в тождество.
График функции в этом случае называется интегральной кривой.
Процесс нахождения решений данного дифференциального уравнения называется интегрированием этого уравнения.
Слайд 12

Задача Коши
Задача отыскания решения дифференциального уравнения, удовлетворяющего заданному начальному условию ,
называется задачей Коши.
Задача Коши:
Слайд 13

Общее решение ДУ
Общим решением дифференциального уравнения
называется такая функция
где –
C произвольная постоянная, что при любом конкретном C она является решением дифференциального уравнения;
для любого допустимого начального условия
найдется такое , что
Слайд 14

Если общее решение записать в виде
то это соотношение называется
общим интегралом дифференциального уравнения.
Частным решением
дифференциального уравнения первого порядка называется функция
которая получается из общего решения при конкретном значении C.
Слайд 15

Дифференциальные уравнения с разделяющимися переменными
Уравнение вида
Где
– заданные функции,
называется дифференциальным уравнением с разделяющимися переменными.
Слайд 16

Если
то, разделив уравнение (1) на
получим уравнение
которое
называется дифференциальным уравнением с разделенными переменными (коэффициент при есть функция переменной x, при – функция переменной y).
Слайд 17

Общий интеграл полученного уравнения находится почленным интегрированием:
Уравнение
Где – заданные функции,
сводится к уравнению (2).
Нужно положить и разделить переменные
Слайд 18

Схема решения ДУ с разделяющимися переменными
Слайд 19

Слайд 20

Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение вида
Где , ,
– непрерывные
функции, называется линейным неоднородным уравнением первого порядка.
Слайд 21

§2. Дифференциальные уравнения второго порядка
Уравнение вида
или
называется дифференциальным уравнением второго
порядка.
Начальные условия для данного уравнения имеют вид
– некоторые числа.
Слайд 22

Решением уравнения
называется всякая функция , которая при подстановке вместе
с y’ и y’’ в это уравнение обращает его в тождество.
Пример. Показать, что функция
является решением уравнения
Решение.
Слайд 23

Общим решением уравнения
называется функция , зависящая от двух произвольных постоянных
и и такая, что:
1) она является решением уравнения при любых конкретных значениях и ;
2) для любых допустимых начальных условий можно подобрать такие и , что функция будет удовлетворять этим условиям.
Слайд 24

Понижение порядка дифференциальных уравнений
В некоторых частных случаях удается понизить порядок
дифференциального уравнения второго порядка. В итоге дифференциальное уравнение приводится к дифференциальному уравнению первого порядка одного из ранее изученных типов.
Слайд 25

Типы уравнений, допускающих понижение порядка
Уравнение
Способ понижения порядка
Слайд 26

Пример
Найти общее решение уравнения
Решение. Интегрируя, получим
– уравнение с
разделяющимися переменными.
Слайд 27

Так как
разделяем переменные и интегрируем:
Слайд 28

ИНТЕГРИРОВАНИЕ ДУ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Уравнение вида
(p и q
– постоянные) называется линейным однородным дифференциальным уравнением с постоянными коэффициентами.
Слайд 29

Уравнение
называется характеристическим для дифференциального уравнения
Для составления характеристического уравнения в
уравнении (4) заменяют
Вид общего решения этого уравнения определяется корнями характеристического уравнения и .
Слайд 30

Пример
Составить характеристические уравнения для следующих дифференциальных уравнений:
1.
2.
3.
4.
Слайд 31

Слайд 32
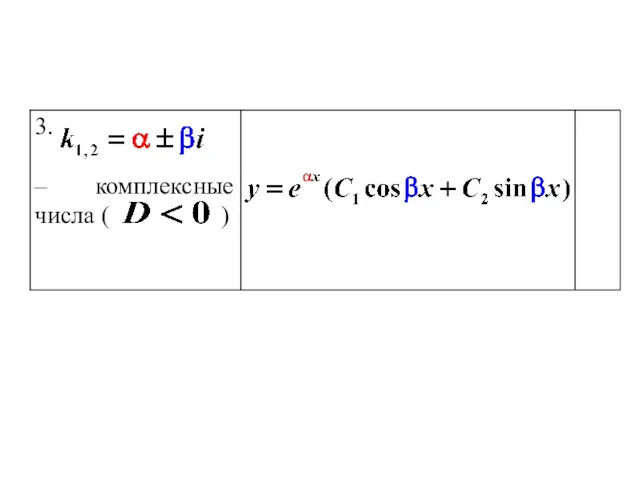
Слайд 33

Пример
1. Найти общее решение уравнения
Решение. Составим характеристическое уравнение, заменяя в данном
уравнении
Получим





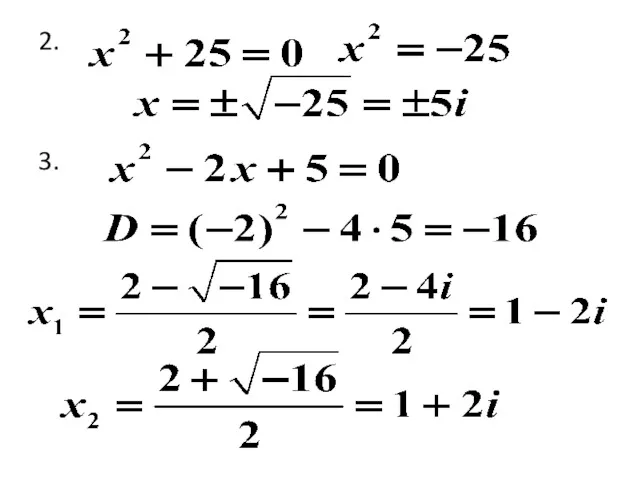
























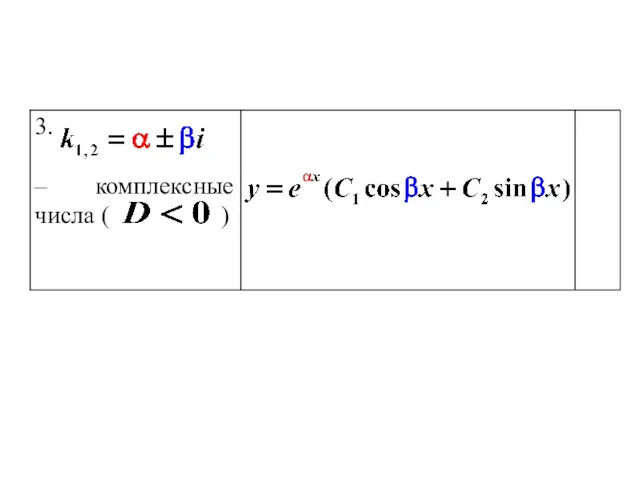

 Геометрия. 7 класс. Измерение отрезков и углов
Геометрия. 7 класс. Измерение отрезков и углов Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Решение задач. (6 класс)
Решение задач. (6 класс) Кеңістік фигураларын жазықтықта бейнелеу. Параллель проекциялау. Ортогональ проекциялау
Кеңістік фигураларын жазықтықта бейнелеу. Параллель проекциялау. Ортогональ проекциялау Многочлен. Вычисление значений многочлена
Многочлен. Вычисление значений многочлена Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел
Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел Методические рекомендации по формированию навыка работы с таблицей (математика 6 класс)
Методические рекомендации по формированию навыка работы с таблицей (математика 6 класс) Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Устный счет
Устный счет Математические модели. Текстовые задачи по математике
Математические модели. Текстовые задачи по математике Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3)
Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3) Устный счёт. Решение выражений
Устный счёт. Решение выражений Самостоятельная математическая деятельность детей дошкольного возраста
Самостоятельная математическая деятельность детей дошкольного возраста Показательная функция
Показательная функция Урок повторения курса геометрии 7-9
Урок повторения курса геометрии 7-9 Задачи (устно)
Задачи (устно) Теория вероятностей. Способность предвидеть возможные варианты будущего
Теория вероятностей. Способность предвидеть возможные варианты будущего Раскрытие скобок
Раскрытие скобок Деление и умножение десятичной дроби (6 класс)
Деление и умножение десятичной дроби (6 класс) Задачи на движение. Скорость
Задачи на движение. Скорость Показательная функция
Показательная функция Интегрированный урок математики с историей
Интегрированный урок математики с историей Внешнее сопряжение двух окружностей
Внешнее сопряжение двух окружностей Ординаты для разбивки переводной кривой стрелочного перевода
Ординаты для разбивки переводной кривой стрелочного перевода 2 Презентация Колличественный счет
2 Презентация Колличественный счет Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Сравнение десятичных дробей
Сравнение десятичных дробей Развитие познавательных способностей.
Развитие познавательных способностей.