Содержание
- 2. Комплексные числа. Действия над комплексными числами.
- 3. Цели занятия: Образовательные: формировать навыки выполнения алгебраических действий над комплексными числами; актуализировать, обобщить и систематизировать знания,
- 4. После изучения темы «Комплексные числа учащиеся должны: Знать: алгебраическую, геометрическую и тригонометрическую формы комплексного числа. Уметь:
- 5. Установите соответствие Натуральные числа Целые числа Рациональные числа Действительные числа Иррациональные числа Z R N Q
- 6. Множества чисел N ⊂ Z ⊂ Q ⊂ R ⊂ C
- 7. Назовите лишнее число в каждой строке. Ответ обоснуйте 1,2(3); 2,455…; 3,1415…; 7,282828… 45; 34; -111; 3,7;
- 8. Найдите ошибки в предложенных классификациях Действительные числа Положительные числа Рациональные числа Бесконечные непериодические дроби Бесконечные периодические
- 9. Бесконечные непериодические дроби Конечные десятичные дроби Неправильные дроби Обыкновенные дроби Бесконечные периодические дроби Составьте классификацию из
- 10. Расположите числа в порядке возрастания
- 11. Для каждой группы чисел найдите в списке правильную характеристику 2; 12; 35; 64 5,1; 4,7; 11,2;
- 12. Найдите ошибки
- 13. Верно ли решены примеры? -8+(-3)=11 48:(-6)=-8 -3·(-7)=-21 3+(-7)=4 -6-10=-16 17+(-21)=-2 -9·3=27 -6:(-3)=-2 -8+(-3)=-11 верно -3·(-7)=21 3+(-7)=-4
- 16. Содержание:
- 17. 1. Мнимая единица
- 18. Допустим, что существует такое число, квадрат которого равен (– 1). Обозначим это число буквой i. Тогда
- 19. Вычислите:
- 20. Пример. Решите уравнение: x2 – 6x + 13 = 0 Решение. Найдем дискриминант по формуле D
- 21. Решите уравнение:
- 22. Название “мнимые числа” ввёл французский математик и философ Р. Декарт в 1637 году
- 23. Степени мнимой единицы
- 25. Значения степеней повторяются с периодом, равным 4. Найдем: Если показатель степени делится на 4 без остатка,
- 26. Решение. i ,– 1, – i , 1 , i, – 1, – i, 1 и
- 27. Вычислите: -1 -i 1 2-i -1
- 28. Комплексные числа Определение 1. Числа вида a + bi, где a и b – действительные числа,
- 29. a + bi = c + di, если a = c и b = d. Свойство:
- 30. Найти x и y из равенства: 3y + 5хi = 15 – 7i Решение: 3y =
- 31. Действия над комплексными числами.
- 32. (а+bi) Вычитание =(a+c) + (c+di) Сложение (b+d) + i (а+bi) - (c+di) =(a-c) + (b-d) i
- 33. Выполните действия: z1 = 2 + 3i, z2 = 5 – 7i. Найти: а) z1 +
- 34. Выполните действие 1. (2 + 3i) + (5 + i) = 2. (– 2 + 3i)
- 35. Умножение (c+di) = ac bс i = + + + аd bd (а+bi) i i2 Учитывая
- 36. Выполните действия: (5 + 3i)(5 – 3i)= (2 + 3i)(5 – 7i) (2 – 7i)2 =
- 37. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
- 38. Деление комплексных чисел. Чтобы выполнить деление, необходимо умножить делимое и делитель на число сопряжённое делителю.
- 39. Деление = = =
- 40. VII в.н.э.- квадратный корень из положительного числа имеет два значения – положительное и отрицательное, а из
- 41. В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных
- 42. Он предложил Кордано назвал такие величины “чисто отрицательными” или даже “софистически отрицательными”, считая их бесполезными и
- 43. в 1572 году итальянский учёный Бомбелли выпустил книгу, в которой были установлены первые правила арифметических операций
- 44. один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare
- 45. гораздо В настоящее время в математике шире, комплексные числа используются действительные чем
- 46. Комплексные числа имеют прикладное значение во многих областях науки, являются основным аппаратом для расчетов в электротехнике
- 47. Применяются при конструировании ракет и самолетов
- 48. При вычерчивании географических карт
- 49. В исследовании течения воды, а также во многих других науках.
- 50. Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда Найти
- 51. Выполните действия:
- 52. Выполните действия:
- 53. Выполните действия: = = = 2
- 54. Домашняя работа 2) Вычислить: 1. (3 + 5i) + (7 – 2i) 2. (– 2 +3i)
- 56. Скачать презентацию





















































 Золотое сечение
Золотое сечение Конспект занятия по формированию элементарных математических представлений Удивительное путешествие
Конспект занятия по формированию элементарных математических представлений Удивительное путешествие Тригонометрические функции острого и тупого углов
Тригонометрические функции острого и тупого углов Системно - деятельностный подход в обучении математике
Системно - деятельностный подход в обучении математике Игровые технологии на уроках математики
Игровые технологии на уроках математики Урок-конференция. Число π
Урок-конференция. Число π Графики тригонометрических функций
Графики тригонометрических функций Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions
Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions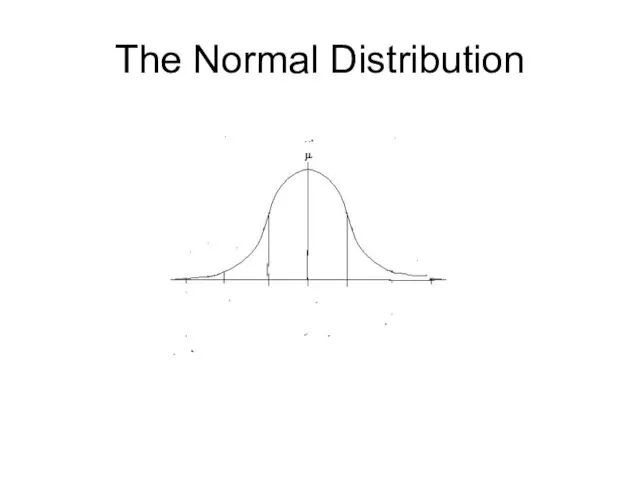 The normal distribution
The normal distribution Плоска система збіжних сил
Плоска система збіжних сил Сложение чисел с разными знаками
Сложение чисел с разными знаками Линейные уравнения. 7 класс
Линейные уравнения. 7 класс Рабочая программа по предметам1класс ФГОС. УМС Занкова.
Рабочая программа по предметам1класс ФГОС. УМС Занкова. Экстремум функции двух переменных
Экстремум функции двух переменных ДЕЛЕНИЕ СУММЫ НА ЧИСЛО. презентация
ДЕЛЕНИЕ СУММЫ НА ЧИСЛО. презентация Статистическое изучение динамики социально-правовых явлений и процессов
Статистическое изучение динамики социально-правовых явлений и процессов Презентация по математике для 1 класса УМК Школа России. По теме: Слагаемые. Сумма.
Презентация по математике для 1 класса УМК Школа России. По теме: Слагаемые. Сумма. Признаки делимости на 2, 5, 10, 4 и 25
Признаки делимости на 2, 5, 10, 4 и 25 Задачи на смекалку
Задачи на смекалку Геометричні перетворення
Геометричні перетворення Решение систем линейных уравнений
Решение систем линейных уравнений Трапеция
Трапеция Умножаем и делим на 7, 8, 9
Умножаем и делим на 7, 8, 9 Слайды к уроку математики в 1 классе.
Слайды к уроку математики в 1 классе. Правило умножения для комбинаторных задач
Правило умножения для комбинаторных задач Подготовка к ЕГЭ. 8 класс. 9 класс. Задания по геометрии. Площади фигур. Декартовы координаты. Векторы
Подготовка к ЕГЭ. 8 класс. 9 класс. Задания по геометрии. Площади фигур. Декартовы координаты. Векторы Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Разработка и программная реализация в ПК МВТУ полной математической модели синхронного генератора в фазных координатах
Разработка и программная реализация в ПК МВТУ полной математической модели синхронного генератора в фазных координатах