Содержание
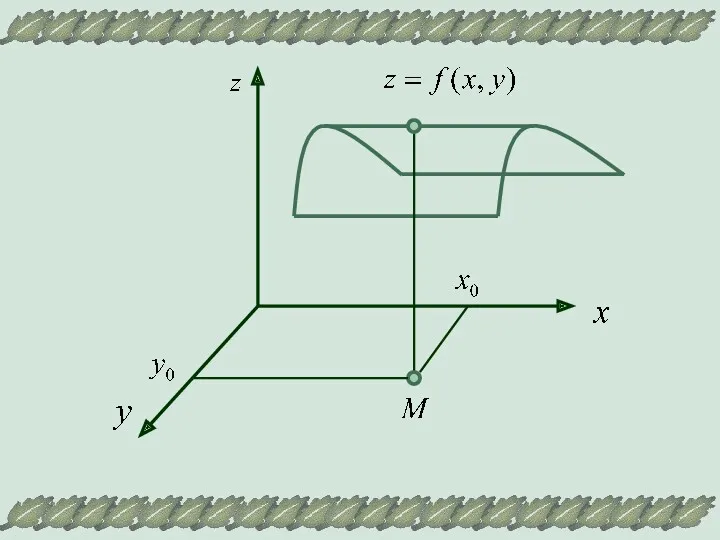
- 2. Точка М(х0,у0) называется точкой максимума (минимума) функции z=f(x,y), если существует окрестность точки М, такая что для
- 3. Экстремум имеет локальный характер, поскольку рассматривается максимальное и минимальное значение функции в достаточно малой окрестности точки
- 4. ТЕОРЕМА. Пусть точка (х0,у0) является точкой экстремума дифференцируемой функции z=f(x,y). Тогда частные производные в этой точке
- 5. Доказательство: Пусть точка М(х0,у0) – точка максимума. Зафиксируем одну из переменных, например, у: у=у0 Тогда получим
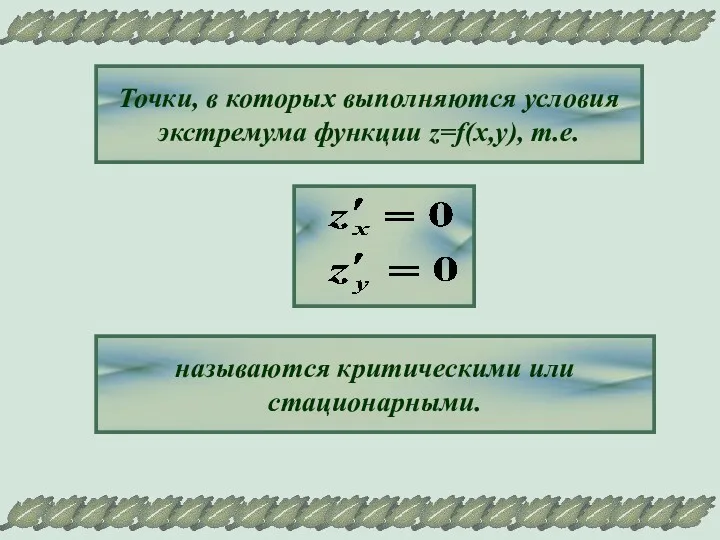
- 6. Точки, в которых выполняются условия экстремума функции z=f(x,y), т.е. называются критическими или стационарными.
- 7. Необходимое условие экстремума можно сформулировать иначе: В точках максимума или минимума дифференцируемой функции градиент этой функции
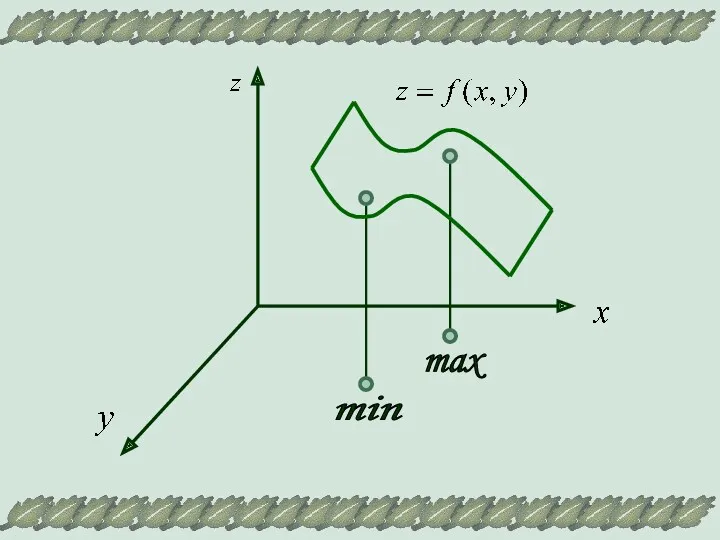
- 8. max min
- 9. Однако, сформулированное выше условие является необходимым, но не достаточным. Т.е., если частные производные функции в точке
- 11. В точке М(х0,у0) выполняется необходимое условие экстремума: Но эта точка не является точкой экстремума. Она называется
- 12. ТЕОРЕМА. Достаточное условие экстремума Пусть функция z=f(x,y) 1 Определена в некоторой окрестности критической точки (х0,у0), в
- 13. 2 Имеет в этой точке непрерывные частные производные второго порядка:
- 14. Тогда, если то в данной точке функция имеет экстремум, причем если А>0, то минимум если А
- 15. СХЕМА исследования функции нескольких переменных на экстремум 1 Найти частные производные
- 16. 2 Решить систему уравнений и найти критические точки
- 17. 3 Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного
- 18. 4 Найти значения функции в точках экстремума.
- 19. Пример. Найти экстремум функции
- 20. Решение.
- 21. Экстремума нет.
- 23. Скачать презентацию















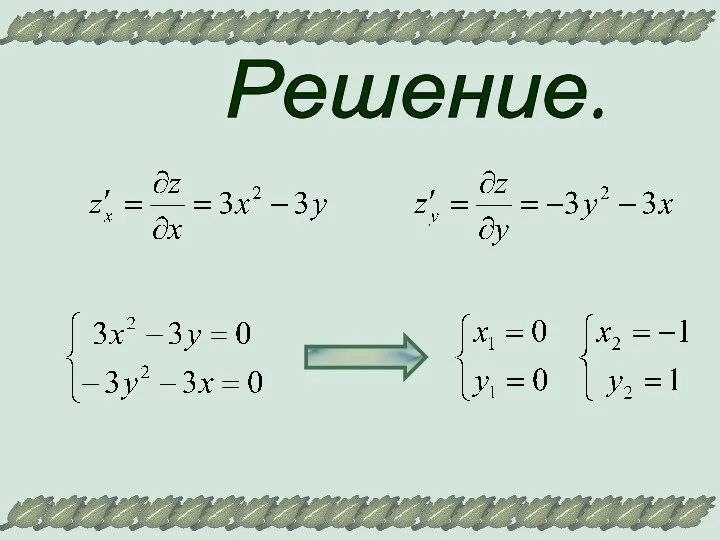
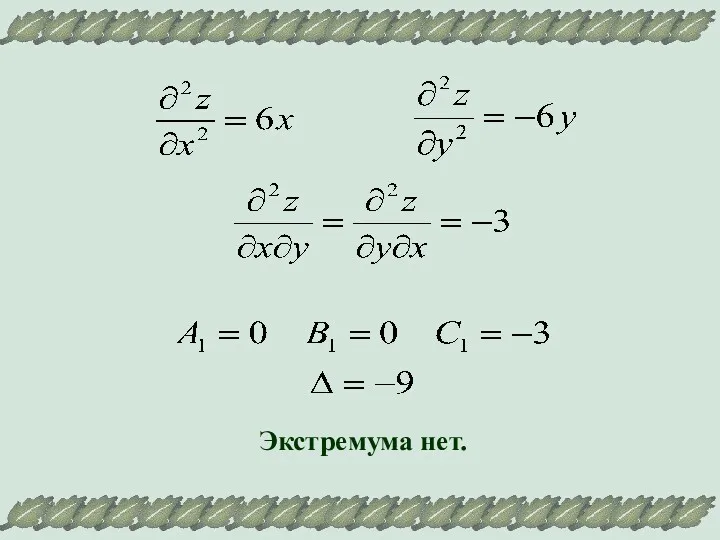
 Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Симметрия. Виды симметрии
Симметрия. Виды симметрии Внеклассное мероприятие по сказке КОЛОБОК
Внеклассное мероприятие по сказке КОЛОБОК Окружность, хорды и диаметры, их свойства
Окружность, хорды и диаметры, их свойства Таблица умножения 3
Таблица умножения 3 Делители и кратные. 5 класс
Делители и кратные. 5 класс Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Презентация по математике Умножение в Простоквашино
Презентация по математике Умножение в Простоквашино Комбинаторика. Правило произведения. Перестановки. Размещения
Комбинаторика. Правило произведения. Перестановки. Размещения Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Правильные многоугольники
Правильные многоугольники Задачи на смеси и сплавы
Задачи на смеси и сплавы Пределы. Числовая последовательность. Предел числовой последовательности
Пределы. Числовая последовательность. Предел числовой последовательности Аксиомы стереометрии. Следствия из аксиом. Задачи
Аксиомы стереометрии. Следствия из аксиом. Задачи Понятие производной
Понятие производной Математика. Основные разделы теста. 1 семестр
Математика. Основные разделы теста. 1 семестр Конус. Конусы вокруг нас
Конус. Конусы вокруг нас Мистика и тайны загадочного числа пи
Мистика и тайны загадочного числа пи Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Теорема Виета. Открытый урок по алгебре. 8 класс
Теорема Виета. Открытый урок по алгебре. 8 класс Сложение однозначных чисел с переходом через десяток вида + 6
Сложение однозначных чисел с переходом через десяток вида + 6 Подготовка к ОГЭ. Функции и графики: линейная функция
Подготовка к ОГЭ. Функции и графики: линейная функция Задачи и принципы квалиметрии
Задачи и принципы квалиметрии Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Подібність трикутників
Подібність трикутників Понятие функции
Понятие функции Задачи по планиметрии
Задачи по планиметрии Цифра 9
Цифра 9