Содержание
- 2. «…très souvent les lois particulières déduites par les physiciens d'un grand nombre d'observations ne sont pas
- 3. Т. (Коши для односвязной области). Пусть в замыкании односвязной области D задана однозначная аналитическая функция f(z).
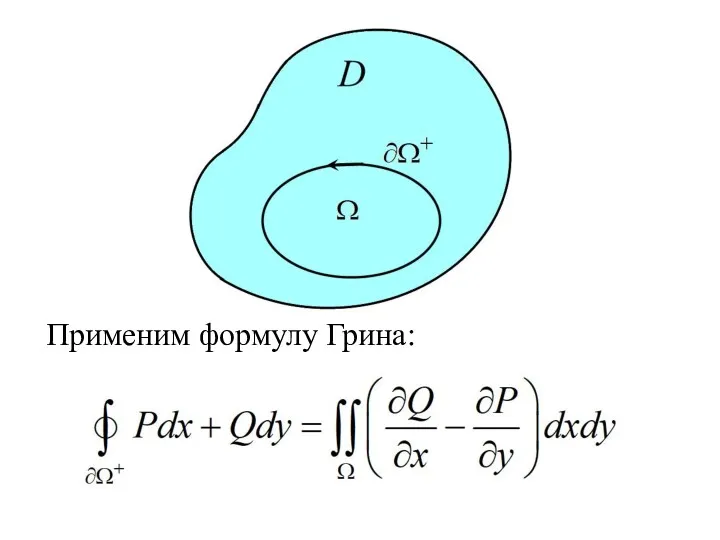
- 4. Применим формулу Грина:
- 5. Получим C учетом условий КРЭД теорема доказана.
- 6. Обобщения теоремы Коши Т. (вторая ф-ка т. Коши) Если функция f(z) является АФ в односвязной области
- 7. Следствие. (аналог ф-лы Ньютона-Лейбница для АФ). Если: кривая интегрирования AB находится в односвязной области, в которой
- 8. Т. (Коши для многосвязной области). Пусть f(z) является аналитической функцией в многосвязной области Ω, ограниченной извне
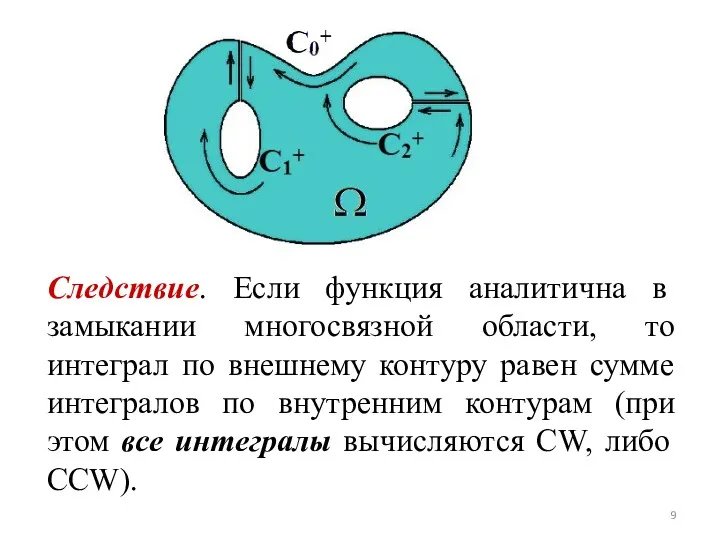
- 9. Следствие. Если функция аналитична в замыкании многосвязной области, то интеграл по внешнему контуру равен сумме интегралов
- 10. П. Вычислить интеграл где C0 – некоторый контур, внутри которого находится точка z = 0.
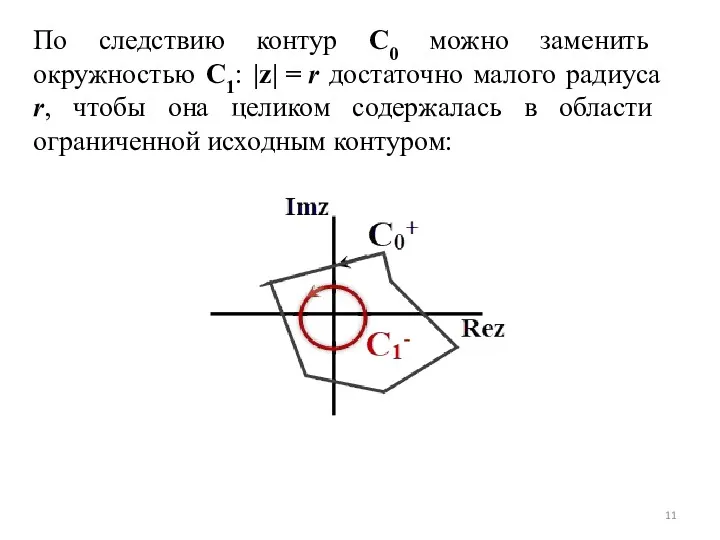
- 11. По следствию контур C0 можно заменить окружностью С1: |z| = r достаточно малого радиуса r, чтобы
- 12. Тогда
- 13. П. Вычислить интеграл где АВ – отрезок прямой, соединяющий точки z=0 и z=1+i. Так как то
- 14. П. Вычислить интеграл где интегрирование может совершаться по любой линии, соединяющей точку ζ = 1 с
- 15. Случай 1. Вдоль пути, не окружающего нулевую точку: Первообразной является многозначная ф-ция
- 16. Для применения формулы НЛ необходимо выбрать какую-либо ветвь этой функции, например, главную (k=0): Случай 2. Путь
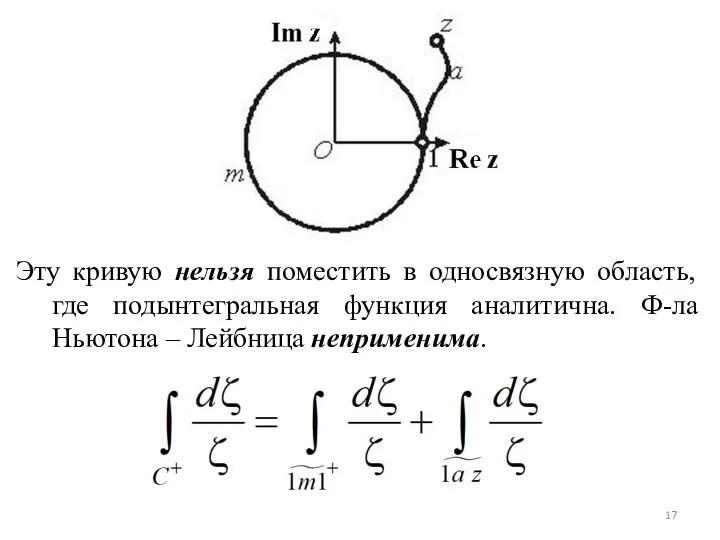
- 17. Эту кривую нельзя поместить в односвязную область, где подынтегральная функция аналитична. Ф-ла Ньютона – Лейбница неприменима.
- 18. Если путь интегрирования делает k оборотов в положительном направлении, то Формула дает интегральное представление функции Lnz
- 19. Т. (формула Коши, интеграл Коши). Пусть функция f(z) аналитична в замыкании области Ω и z0∈Ω –
- 20. Формальное доказательство. Пусть ε – произвольное достаточно малое число, такое, что окружность этого радиуса с центром
- 21. Переходя к пределу при ε→0, получим ч.т.д.
- 22. Следствие. При выполнении условий теоремы Коши АФ имеет производные любого порядка и Замечание. Если т. z0
- 23. Обобщенный вариант формулы Коши: П. Вычислить
- 25. a) Перепишем интеграл в виде:
- 27. Разложим функцию на сумму простых дробей
- 29. П. Вычислить
- 31. Скачать презентацию







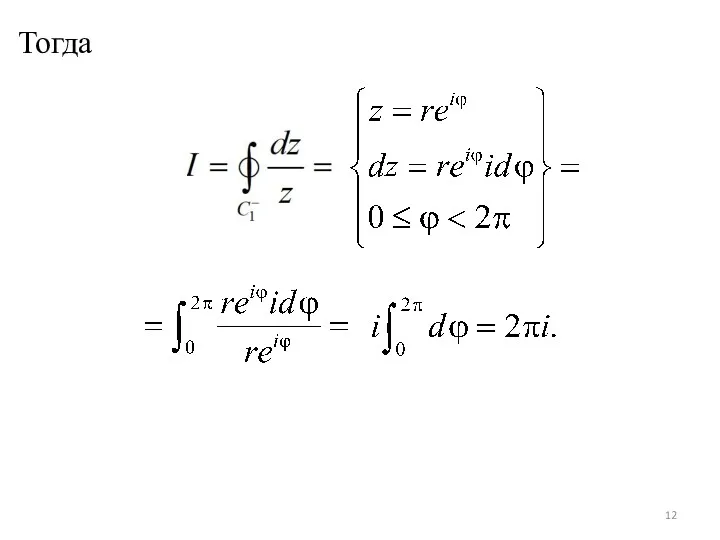











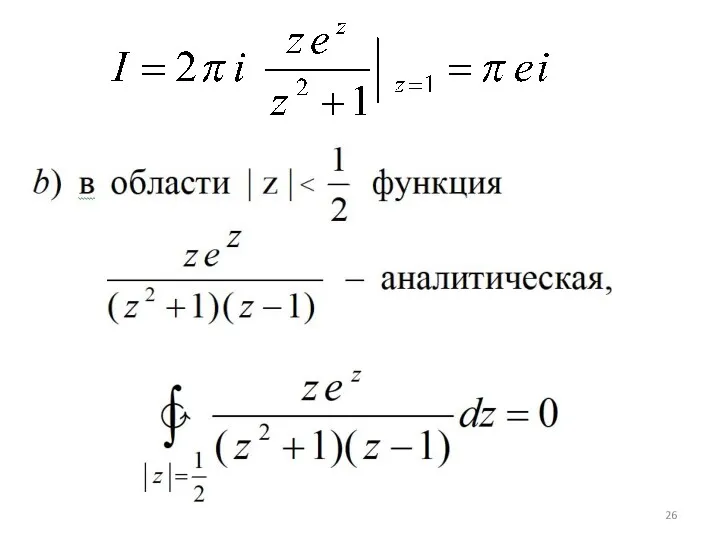

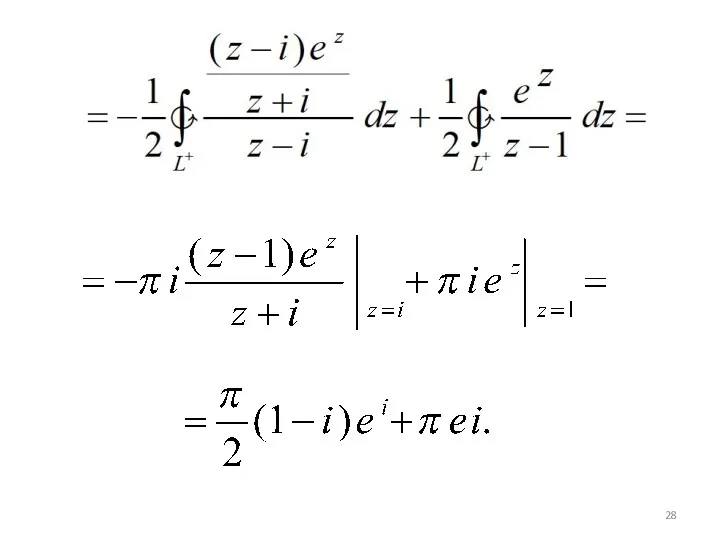
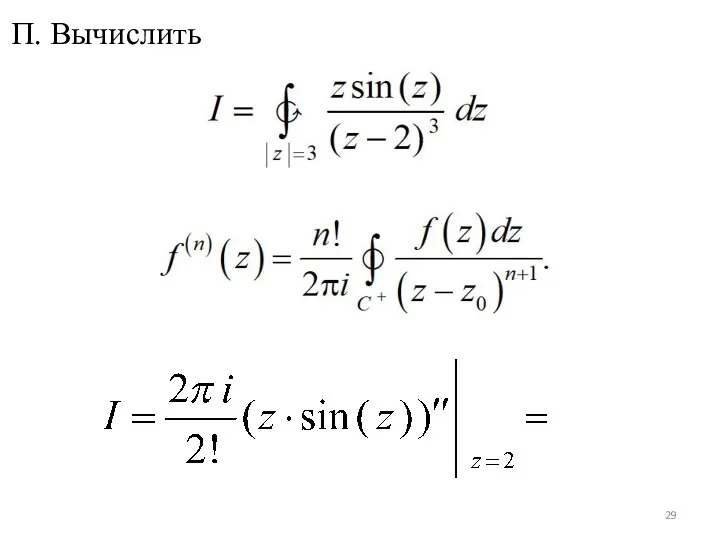
 Анализ данных в Mathcad. Математические вычисления
Анализ данных в Mathcad. Математические вычисления ARCH and GARCH. Modeling Volatility Dynamics
ARCH and GARCH. Modeling Volatility Dynamics История создания величин измерения времени
История создания величин измерения времени Действия с отрицательными и положительными числами на уроках математики и географии
Действия с отрицательными и положительными числами на уроках математики и географии Способы решения задач на смеси и сплавы. Арифметический. Применение уравнения. Применение систем уравнений
Способы решения задач на смеси и сплавы. Арифметический. Применение уравнения. Применение систем уравнений Методы решения систем уравнений. Критерий итерационной сходимости
Методы решения систем уравнений. Критерий итерационной сходимости Использование художественного произведений при обучении детей математике. Количество-1.
Использование художественного произведений при обучении детей математике. Количество-1. Система уравнений с двумя переменными
Система уравнений с двумя переменными Преобразование выражений. 7 класс
Преобразование выражений. 7 класс Математика в профессии автомеханика
Математика в профессии автомеханика В помощь 1-м курсам по созданию проекта по математике
В помощь 1-м курсам по созданию проекта по математике Смежные и вертикальные углы
Смежные и вертикальные углы Нумерація трицифрових чисел
Нумерація трицифрових чисел Презентация по математике Площадь прямоугольника для 4 класса
Презентация по математике Площадь прямоугольника для 4 класса Неделя математики
Неделя математики Задачи на движение. Повторение
Задачи на движение. Повторение Морской бой. Игра
Морской бой. Игра Тренажёр Действия с круглыми числами
Тренажёр Действия с круглыми числами Тренажер «Умножение целых чисел»
Тренажер «Умножение целых чисел» Дециметр. Урок математики 1 класс
Дециметр. Урок математики 1 класс Формулы двойного аргумента
Формулы двойного аргумента Пропорция. Урок математики в 6 классе
Пропорция. Урок математики в 6 классе Сложение чисел с разными знаками
Сложение чисел с разными знаками Решение задач
Решение задач Построение сечений многогранников
Построение сечений многогранников Методы оптимальных решений. Принятие решений на основе метода анализа иерархий
Методы оптимальных решений. Принятие решений на основе метода анализа иерархий Взаимосвязь математики и архитектуры
Взаимосвязь математики и архитектуры Математика+Габдулла Тукай
Математика+Габдулла Тукай