Содержание
- 2. Исследование функций с помощью производной Одним из приложений производной является применение производной к исследованию функции и
- 3. Экстремум функции Пусть y = f(x) непрерывна на интервале (a, b), х0∈ (a, b). Точка х0
- 4. Теорема 2 (необходимое условие экстремума). Пусть функция y = f(x) имеет экстремум в точке х0. Тогда
- 5. Гладкие экстремумы Острые экстремумы
- 6. Для исследования критической точки на экстремум используют первое или второе достаточное условие экстремума Теорема 3 (первое
- 7. Выпуклость и вогнутость. Точки перегиба Пусть кривая y = f(x), x∈ (a, b) имеет в любой
- 8. Теорема 5 (условие выпуклости / вогнутости). Если ∀x∈ (a, b) f ″(x) Если ∀x∈ (a, b)
- 9. Для исследования кривой y = f(x) на выпуклость (вогнутость) и точки перегиба нужно 1. найти точки,
- 10. Асимптоты графика функции Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится
- 11. Вертикальная асимптота Если то прямая х = х0 является вертикальной асимптотой кривой y = f(x). Если
- 12. Невертикальная асимптота Теорема 8. Кривая y = f(x) имеет невертикальную асимптоту y = kx + b
- 13. х = 0 вертикальная асимптота у = 0 горизонтальная асимптота х = 1 вертикальная асимптота y
- 14. у = 0 горизонтальная асимптота при х → + ∞; при х → − ∞ кривая
- 15. Схема исследования функции и построение ее графика При построении графика функции в общем случае можно использовать
- 16. Пункты 1-6 определяют полную схему исследования. Если график не совсем понятен и после выполнения всех пунктов
- 18. Скачать презентацию
 Случайные процессы (лекция 13). Закон распределения и основные характеристики случайных процессов
Случайные процессы (лекция 13). Закон распределения и основные характеристики случайных процессов Основы сетевого планирования и управления (СПУ) разработками
Основы сетевого планирования и управления (СПУ) разработками Приближенные методы вычислений
Приближенные методы вычислений Двузначные числа
Двузначные числа Формулы сокращённого умножения. 7 класс
Формулы сокращённого умножения. 7 класс Сокращение дробей. Упражнение 6
Сокращение дробей. Упражнение 6 Математика 2 класс Формирование вычислительных навыков.Обобщение и закрепление изученного Презентация
Математика 2 класс Формирование вычислительных навыков.Обобщение и закрепление изученного Презентация Задачи экономического содержания на ЕГЭ по математике
Задачи экономического содержания на ЕГЭ по математике CENG 789 – Digital Geometry Processing
CENG 789 – Digital Geometry Processing Окружность – замкнутая линия
Окружность – замкнутая линия ГИА – ОГЭ 9. Открытый банк заданий по математике
ГИА – ОГЭ 9. Открытый банк заданий по математике Производная по направлению. Градиент
Производная по направлению. Градиент Относительность движения. 9 класс
Относительность движения. 9 класс Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Деление дробей
Деление дробей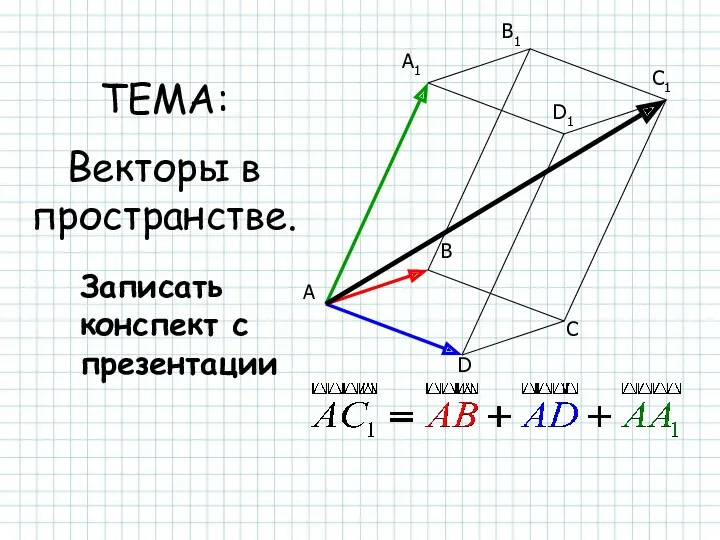 Векторы в пространстве
Векторы в пространстве Урок-игра по математике Путешествие в сказку
Урок-игра по математике Путешествие в сказку Буквенные и числовые выражения
Буквенные и числовые выражения Площадь криволинейной трапеции
Площадь криволинейной трапеции Отрезок. Измерение отрезков
Отрезок. Измерение отрезков Разность квадратов двух выражений
Разность квадратов двух выражений Логическое следование формул алгебры предикатов
Логическое следование формул алгебры предикатов Случаи вычитания 11-
Случаи вычитания 11- Интерактивная игра Найди ошибку
Интерактивная игра Найди ошибку Тренажёр У кого Карлсон в гостях?
Тренажёр У кого Карлсон в гостях? Уравнение прямой на плоскости
Уравнение прямой на плоскости урок математики
урок математики Делители и кратные
Делители и кратные