Слайд 2

1. Нелинейные уравнения. Понятия и определения
Уравнение вида: f(x)=0, если f(x) не
является многочленом 1-ой степени, называется нелинейным или трансцедентным.
Всякое x=x*, обращающее в 0 уравнение, есть его корень.
Решение состоит из 2-х этапов:
а) отделение корней (изолированные корни);
б) уточнение корней.
Слайд 3
![а): Теорема 1 Если, непрерывная на отрезке [a;b] функция f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366038/slide-2.jpg)
а):
Теорема 1
Если, непрерывная на отрезке [a;b] функция f(x) на его краях
принимает разные значения, т.е. f(a)f(b)<0, то внутри этого отрезка существует хотя бы один корень уравнения f(x)=0.
Корень единственный, если производная f/(x) сохраняет знак внутри интервала (a;b).
Слайд 4

Алгоритм отделения корней:
определяются граничные точки x=a, x=b области существования f(x);
вычисляются значения
функции f(x) на [a;b] с шагом h до смены знака функции при переходе от f(x) до f(x+h) (шаг выбирается с учетом особенностей функции);
Слайд 5

б):
Уточнение корней заключается в поиске приближенного корня xn, при котором:
f(xn)<ε,
(5.1)
где ε- заданная точность определения корней (для точного корня x* выполняется f(x)=0).
Теорема 2
Для точного x* и приближенного xn корней нелинейного уравнения, принадлежащих отрезку [a;b], модуль производной функции на этом отрезке всегда больше некоторого m1.
Слайд 6

б):
Тогда, точность отыскания корней определяется:
| xn - x* |< f/(x)
/m1 (5.2)
Методы уточнения корней (решения) нелинейных уравнений:
метод половинного деления;
метод простой итерации;
метод касательных (метод Ньютона - Рафсона).
Слайд 7

2. Метод половинного деления.
Постановка задачи: уточнить корни уравнения f(x)=0, на
отрезке [a;b].
Алгоритм:
выбирается середина отрезка C=(a+b)/2;
проверка условия окончания f(с)=0 или
|b-a|/2n определение отрезка [a;c] или [c;b], на концах которого значения функции имеют разные знаки;
повторение итераций.
Слайд 8
![Пример: Уточнить корень уравнения x4+2x3-x-1=0, принадлежащий отрезку [0;1]. Сделать 6 итераций.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366038/slide-7.jpg)
Пример:
Уточнить корень уравнения x4+2x3-x-1=0, принадлежащий отрезку [0;1]. Сделать 6 итераций.
Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

3. Решение нелинейных уравнений методом итерации.
Уравнение f(x)=0 должно удовлетворять условиям:
f(x)
должна быть дифференцируема на [a,b];
f(x) должна принимать разные значения на краях интервала: f(a)f(b)<0 (тогда внутри интервала имеется хотя бы один корень уравнения);
f(x)=0 на [a,b] (если производная внутри интервала не меняет знак, то корень один);
Слайд 14

Метод заключается в том, что:
а)заменяется уравнение f(x)=0 на равносильное ему уравнение
вида x=φ(x);
б)произвольно выбирается начальное значение x0 ∈ [a,b];
в)вычисляются итерации:
x1 =φ(x0);
x2 =φ(x1);
………………..
xn+1 =φ(xn); n=0,1…..
Слайд 15

г)проверяется выполнение условий сходимости:
Теорема: процесс итерации xn+1=φ(xn) сходится не зависимо от
выбора начального значения x0 ∈ [a,b] и предельное значение x*=limn→∞xn – единственный корень уравнения x=φ(x) на [a,b], если:
все значения φ(x)∈[a,b] и она дифференцируема на этом отрезке;
существует правильная дробь q, такая, что |φ(x)|≤q<1.
Слайд 16

Алгоритм метода итераций:
А) исходное уравнение заменяется функцией вида φ(x)=λf(x)+x, где: (1)
-1/r<λ<0 при f(x)>0;
0<λ<1/r при f(x)<0;
r=max(|f(a)|,|f(b)|).
Б) выбирается начальное значение x0∈[a,b].
В) в (1) по условиям после вычисления r выбирается λ и составляется рекурентная формула метода итерации вида:
Xn+1=λf(xn)+xn
Слайд 17

Г) Проверяются условия сходимости:
∆x=|x*-xn|≤m/(1-q)qm, (2)
где m= |xn- φ(xn)|; q=| φ(xn) |.
Процесс
вычисления (пункты в, г) повторяется до тех пор, пока не достигается заданная точность решения Е, т.е. расчеты прекращаются, когда выполнится неравенство (пункт г):
∆x≤Е.
Слайд 18

4. Решение нелинейных уравнений методом Ньютона-Рафсона.
Для решения уравнения вида f(x)=0
формула метода Ньютона-Рафсона:
xn+1= xn- f(xn)
f(xn) (1)
Возможность применения метода определяется теоремой:
если на интервале [a;b] функция F(x)=f(x)-x дважды дифференцируема и на краях интервала принимает различные по знаку значения F(a)F(b)<0, то исходя из начального
Слайд 19

приближения, отвечающего условию:
F(x0)F(x)>0, (2)
можно вычислить методом Ньютона-Рафсона единственный корень уравнения
с любой заданной точностью.
Из теоремы следует, что F(x)=f(x)-x на интервале [a;b] должна удовлетворять следующим требованиям:
должна быть определена и непрерывна;
на краях принимать противоположные по знаку значения F(a)F(b)<0;
Слайд 20

F(x) ≢0;
F (x) существует и сохраняет знак (следовательно, на [a;b] только
один корень);
если F(x) в окрестности корня x* имеет производную близкую к нулю (корень-экстремум функции), то применение метода дает неудовлетворительный результат.
Погрешность оценивается как:
|xn- xn-1|≤ 2min|F(x)|E/max|F (x)|; (3)
Слайд 21

Алгоритм метода Ньютона-Рафсона :
А) определяются 1-я и 2-я производные, их знаки,
минимальное для 1-ой и максимальное для 2-ой производных значения на отрезке [a,b] (с помощью Excel);
Б) выбирается начальное значение x0 из условия (2), т.е. если это условие выполняется и на [a,b] 2-я производная сохраняет знак, то x0 может быть любым;
В) по рекурентной формуле (1) вычисляется значение корня;
Г) по соотношению (3) оценивается погрешность: если условие выполняется,

![а): Теорема 1 Если, непрерывная на отрезке [a;b] функция f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366038/slide-2.jpg)




![Пример: Уточнить корень уравнения x4+2x3-x-1=0, принадлежащий отрезку [0;1]. Сделать 6 итераций.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366038/slide-7.jpg)













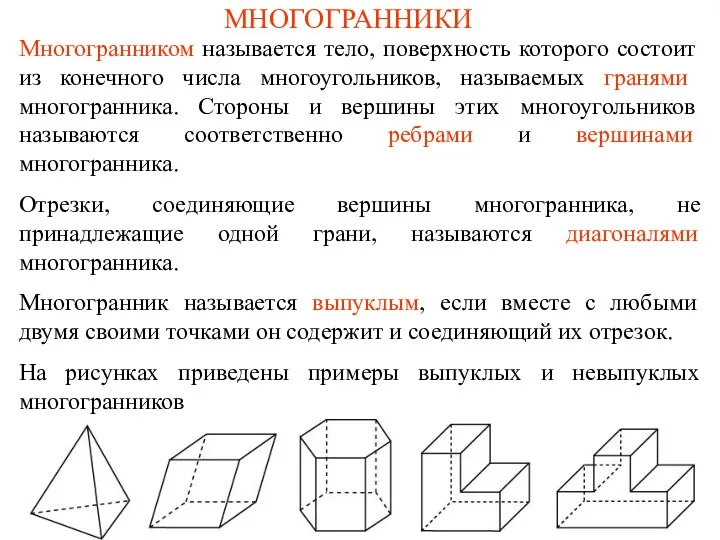 Фигуры в пространстве
Фигуры в пространстве Итоговый тест по математике
Итоговый тест по математике Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции Системы уравнений. Способы решения
Системы уравнений. Способы решения Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Приёмы устных вычислений вида 470 + 80, 560 - 90
Приёмы устных вычислений вида 470 + 80, 560 - 90 Математика в Древнем Египте
Математика в Древнем Египте Устный счет (4 класс)
Устный счет (4 класс) Математическое странствие
Математическое странствие Типы оперирования
Типы оперирования Сложность вычислений
Сложность вычислений Time quiz
Time quiz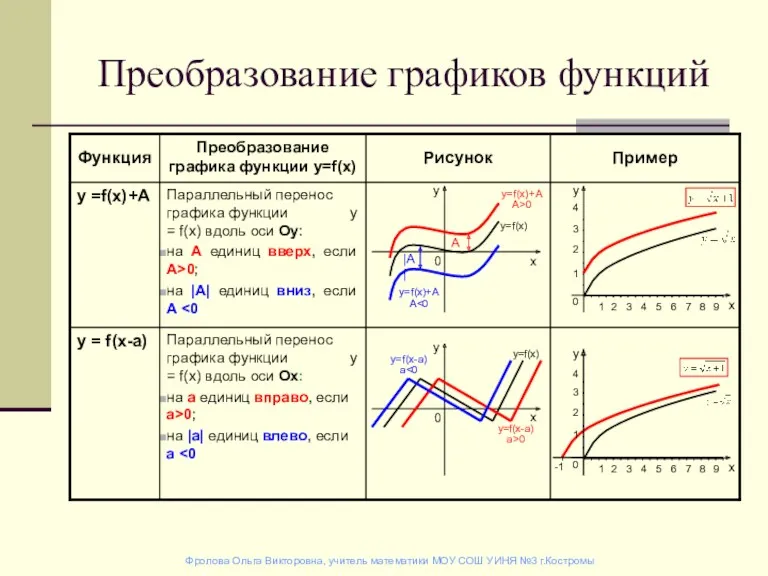 Преобразование графиков функций
Преобразование графиков функций Математика. Решение задач
Математика. Решение задач Описательные статистики
Описательные статистики Сложение и вычитание в пределах 20 (апрель 2014 год).
Сложение и вычитание в пределах 20 (апрель 2014 год). Преобразование графиков функций
Преобразование графиков функций Число и цифра 2.
Число и цифра 2. Интеллектуальный марафон
Интеллектуальный марафон Простые числа. Разложение числа на множители
Простые числа. Разложение числа на множители Решение уравнений и задач с помощью уравнений. 6 класс
Решение уравнений и задач с помощью уравнений. 6 класс Математическая сказка Диск
Математическая сказка Диск Что такое геометрия?
Что такое геометрия? Прямая и обратная пропорциональная зависимости. 6 класс
Прямая и обратная пропорциональная зависимости. 6 класс Применение теории графов к решению задач
Применение теории графов к решению задач Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Сказочная страна функций. Электронный урок
Сказочная страна функций. Электронный урок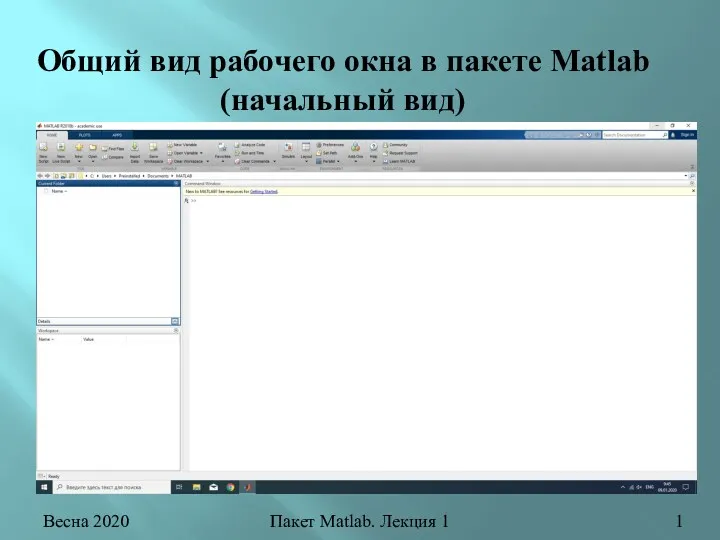 Введение в Mathlab
Введение в Mathlab