Содержание
- 2. 1. Обзор методов численного нтегрирования Задача численного интегрирования- вычислить интеграл используя ряд значений подинтегральной функции y=f(x),
- 3. Методы сплайн – интегрирования основаны на аппроксимации подинтегральной функции сплайнами – функциями, форма которых близка к
- 4. Методы Ньютона-Котеса предусматривают разбиение интервала интегрирования [a,b] на n равных частей с шагом: h=xi+1- xi=(b-a)/n, i=1,n
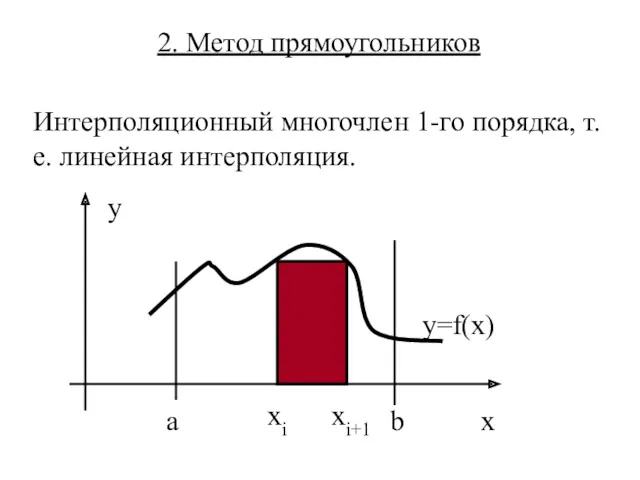
- 5. 2. Метод прямоугольников Интерполяционный многочлен 1-го порядка, т.е. линейная интерполяция.
- 6. (6) Если узел α=а- левому краю отрезка интегрирования, то (6) – формула «левых» прямоугольников; Если узел
- 7. (7) Погрешности:
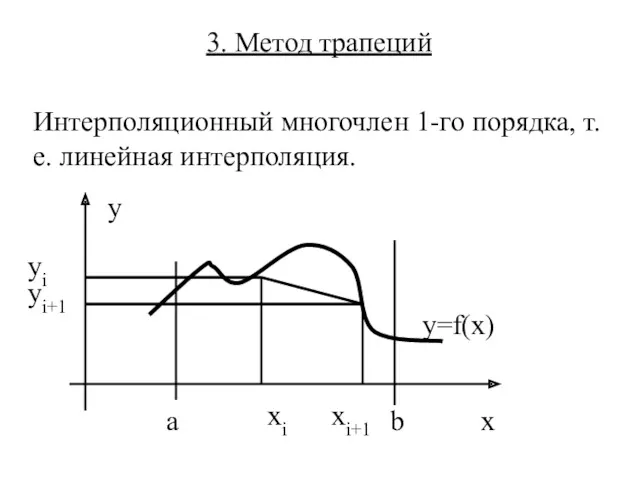
- 8. 3. Метод трапеций Интерполяционный многочлен 1-го порядка, т.е. линейная интерполяция.
- 9. (8) Погрешность: (9)
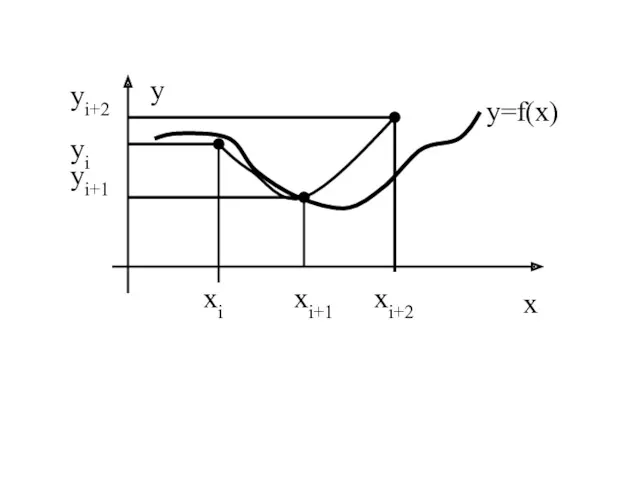
- 10. 4. Метод Симпсона. Описание метода. (1) При этом, необходимым условием является то, что количество интервалов разбиения
- 11. y x y=f(x) xi xi+1 yi+1 yi xi+2 yi+2
- 12. Погрешность метода Симпсона: где: (3)
- 14. Скачать презентацию


![Методы Ньютона-Котеса предусматривают разбиение интервала интегрирования [a,b] на n равных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/143946/slide-3.jpg)

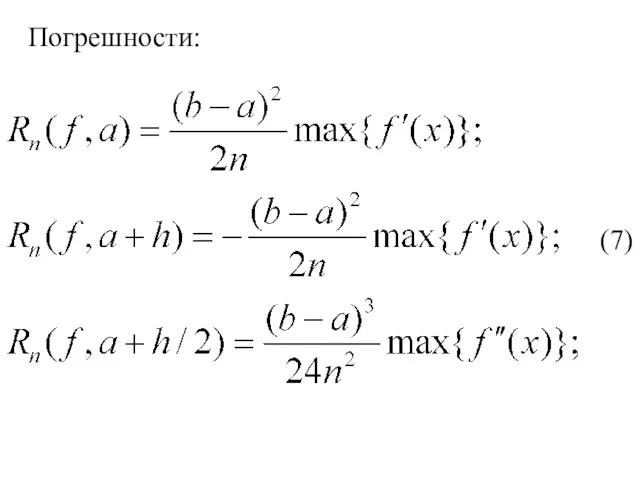
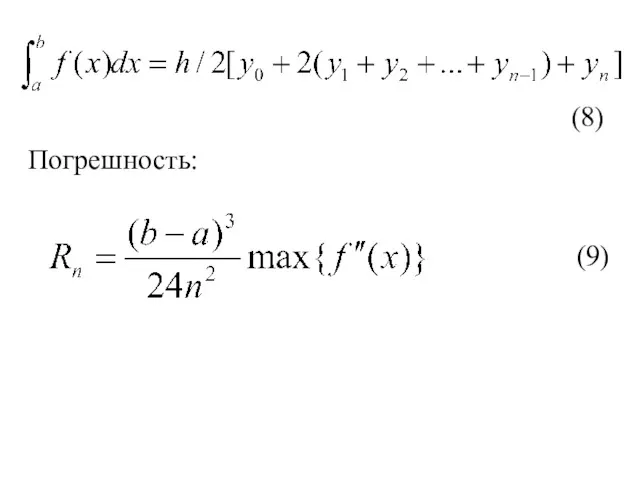


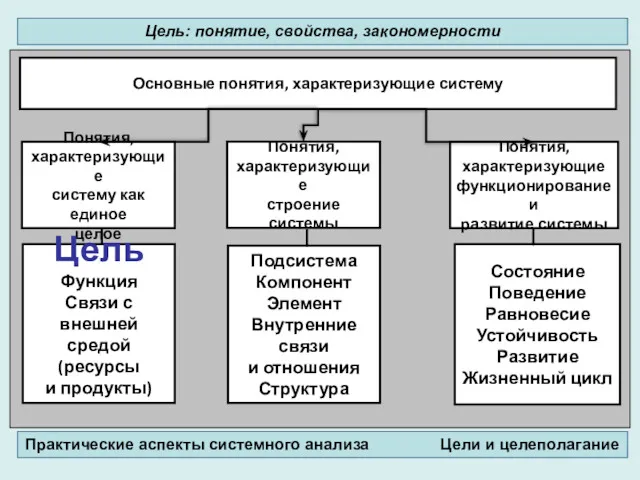 Понятие, свойства, закономерности. Основные понятия, характеризующие систему, как единое целое
Понятие, свойства, закономерности. Основные понятия, характеризующие систему, как единое целое Методы решения систем уравнений. Метод подстановки
Методы решения систем уравнений. Метод подстановки презентация по математике
презентация по математике Смешанные числа. 5 класс
Смешанные числа. 5 класс Понятие логарифма
Понятие логарифма Формирование временных представлений у младших школьников
Формирование временных представлений у младших школьников Координати та вектори в просторі
Координати та вектори в просторі Число и цифра 9
Число и цифра 9 Презентация к уроку математики с элементами экологии.
Презентация к уроку математики с элементами экологии. Контрольная работа по математике 3 класс,3 четверть, Занков
Контрольная работа по математике 3 класс,3 четверть, Занков Многоугольники
Многоугольники Масса. Методика преподавания математики
Масса. Методика преподавания математики Усеченная пирамида
Усеченная пирамида Свойства действий с рациональными числами
Свойства действий с рациональными числами Кривые второго порядка. Лекция 7
Кривые второго порядка. Лекция 7 История науки алгебры
История науки алгебры Задачи ОГЭ и ЕГЭ по геометрии
Задачи ОГЭ и ЕГЭ по геометрии Действия с квадратными корнями
Действия с квадратными корнями презентация единицы времени
презентация единицы времени Теорема Виета 1
Теорема Виета 1 Презентация по теме Доли и дроби 4 класс
Презентация по теме Доли и дроби 4 класс Веселая геометрия
Веселая геометрия Полуправильные многогранники
Полуправильные многогранники Производная и первообразная. Задание 7 ЕГЭ профильной математики
Производная и первообразная. Задание 7 ЕГЭ профильной математики Конструктивная деятельность на занятиях по математике.
Конструктивная деятельность на занятиях по математике. Пересечение и объединение множеств
Пересечение и объединение множеств Урок по математике Название компонентов и результата деления.
Урок по математике Название компонентов и результата деления. Осевая и центральная симметрия. Симметрия в природе
Осевая и центральная симметрия. Симметрия в природе