Содержание
- 2. First, a Word About Hammers requirements for this to be a good idea a way of
- 3. Hammers (cont.) by definition, not the optimal way to solve problems, BUT computers are very fast
- 4. What are “advanced game math problems”? problems that are ammenable to mathematical modeling state the problem
- 5. Prerequisites linear algebra vector, matrix symbol manipulation at least calculus concepts what derivatives mean comfortable with
- 6. Overview of Lecture random assortment of example problems breifly mentioned 5 specific example problems in some
- 7. A Look Forward linear equations Ax = b linear inequalities Ax >= b linear programming min
- 8. Applications to Games graphics, physics, ai, even ui computational geometry visibility contact curve fitting constraints integration
- 9. Applications to Games (cont.) don’t forget... The Elastohydrodynamic Lubrication Problem Solving Optimal Ownership Structures “The two
- 10. Specific Examples #1a: Ease Cubic Fitting warm up with an ease curve cubic x(t)=at3+bt2+ct+d x’(t)=3at2+2bt+c 4
- 11. Specific Examples #1a: Ease Cubic Fitting (cont.) x(t)=at3+bt2+ct+d, x’(t)=3at2+2bt+c x(0) = a03+b02+c0+d = d = 0
- 12. Specific Examples #1a: Ease Cubic Fitting (cont.) d = 0, a+b+c+d = 1, c = 0,
- 13. Specific Examples #1a: Ease Cubic Fitting (cont.) or, x(0) = d = 0 x(1) = a
- 14. Specific Examples #1b: Cubic Spline Fitting same technique to fit higher order polynomials, but they “wiggle”
- 15. Specific Examples #1b: Cubic Spline Fitting (cont.) a0 b0 c0 d0 a1 b1 c1 d1 .
- 16. Specific Examples #2: Minimum Cost Network Flow what is the cheapest flow route(s) from sources to
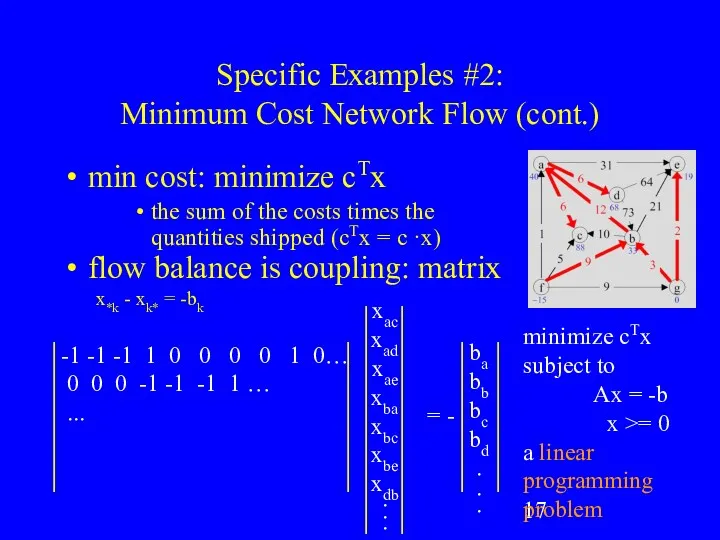
- 17. Specific Examples #2: Minimum Cost Network Flow (cont.) min cost: minimize cTx the sum of the
- 18. Specific Examples #3: Points in Polys point in convex poly defined by planes n1 · x
- 19. Specific Examples #3: Points in Polys (cont.) closest point in two polys min (x2-x1)2 s.t. A1x1
- 20. Specific Examples #3: Points in Polys (cont.) how do we stack x1,x2 into single x given
- 21. Specific Examples #3: Points in Polys (cont.) more points, more polys! min (x2-x1)2 + (x3-x2)2 +
- 22. Specific Examples #4: Contact model like IK constraints a = Af + b a >= 0,
- 23. Specific Examples #5: Joint Limits in CCD IK how to do child-child constraints in CCD? parent-child
- 24. What Unifies These Examples? linear equations Ax = b linear inequalities Ax >= b linear programming
- 25. QP is a Superset of Most quadratic programming min ½xTQx + cTx s.t. Ax >= b
- 26. Karush-Kuhn-Tucker Optimality Conditions get us to MLCP for QP form “Lagrangian” L(x,u,v) = ½ xTQx +
- 27. Karush-Kuhn-Tucker Optimality Conditions (cont.) L(x,u,v) = ½ xTQx + cTx - uT(Ax - b) - vT(Dx
- 28. This is an MLCP x v u Q -DT -AT D 0 0 A 0 0
- 29. Modeling Summary a lot of interesting problems can be formulated as MLCPs model the problem mathematically
- 30. Solving MLCPs (where I hope I made you hungry enough for homework) Lemke’s Algorithm is only
- 31. Playing Around With MLCPs PATH, a MCP solver (superset of MLCP!) really stoked professional solver free
- 32. References for Lemke, etc. free pdf book by Katta Murty on LCPs, etc. free pdf book
- 34. Specific Examples #5: Constraints for IK compute “forces” to keep bones together a1 = A11 f1
- 36. Скачать презентацию
































 Треугольники. Задачи
Треугольники. Задачи Метод координат при решении стереометрических задач. Урок геометрии, 11 класс
Метод координат при решении стереометрических задач. Урок геометрии, 11 класс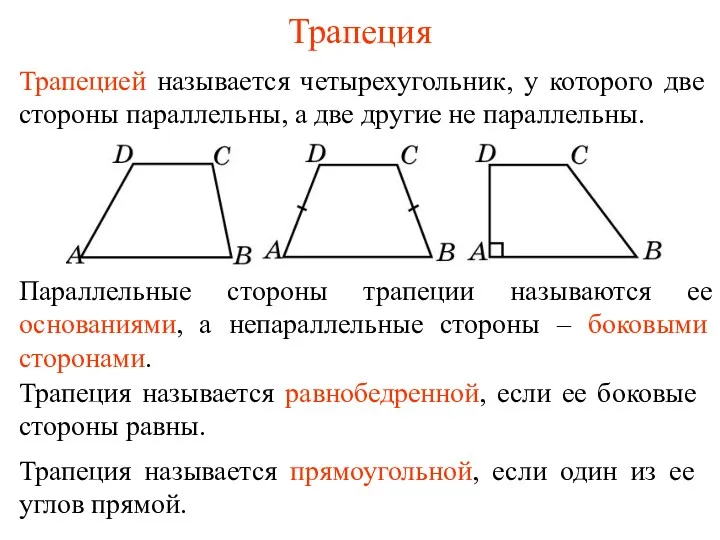 Трапеция. Теорема о средней линии трапеции
Трапеция. Теорема о средней линии трапеции Признаки делимости чисел на 2, 3, 9
Признаки делимости чисел на 2, 3, 9 Конус. Элементы конуса. Сечение конуса
Конус. Элементы конуса. Сечение конуса Координатная прямая
Координатная прямая Сложная функция. 10 класс
Сложная функция. 10 класс презентации и конспекты уроков
презентации и конспекты уроков Прогрессии вокруг нас. (9 класс)
Прогрессии вокруг нас. (9 класс) Число и цифра 4
Число и цифра 4 Презентация по математике тема: Часы, минуты, сутки (подготовительная группа)
Презентация по математике тема: Часы, минуты, сутки (подготовительная группа) Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Измерение углов
Измерение углов Цилиндр
Цилиндр Производная функции. Возрастание и убывание функций
Производная функции. Возрастание и убывание функций Интеллектуальная математическая игра для 6 класса
Интеллектуальная математическая игра для 6 класса Сложение и вычитание в пределах 20 2 класс УМК Школа 2100
Сложение и вычитание в пределах 20 2 класс УМК Школа 2100 Урок математики Движение с отставанием 4 класс Петерсон Л. Г.
Урок математики Движение с отставанием 4 класс Петерсон Л. Г. Численные методы
Численные методы Признаки параллельности прямых
Признаки параллельности прямых Квадратный корень. Арифметический квадратный корень
Квадратный корень. Арифметический квадратный корень Розкладання квадратного тричлена на множники
Розкладання квадратного тричлена на множники Площадь фигуры
Площадь фигуры Плоские фигуры - многоугольники. Объемные фигуры
Плоские фигуры - многоугольники. Объемные фигуры Функция. Область определения и область значений функции. 7 класс
Функция. Область определения и область значений функции. 7 класс Презентация к уроку математики Зимние забавы
Презентация к уроку математики Зимние забавы Линейная модель парной регрессии. Метод наименьших квадратов
Линейная модель парной регрессии. Метод наименьших квадратов Начальные геометрические сведения. Прямая и отрезок
Начальные геометрические сведения. Прямая и отрезок