Содержание
- 2. Возрастание и убывание функций Одним из приложений производной является ее применение к исследованию функций и построению
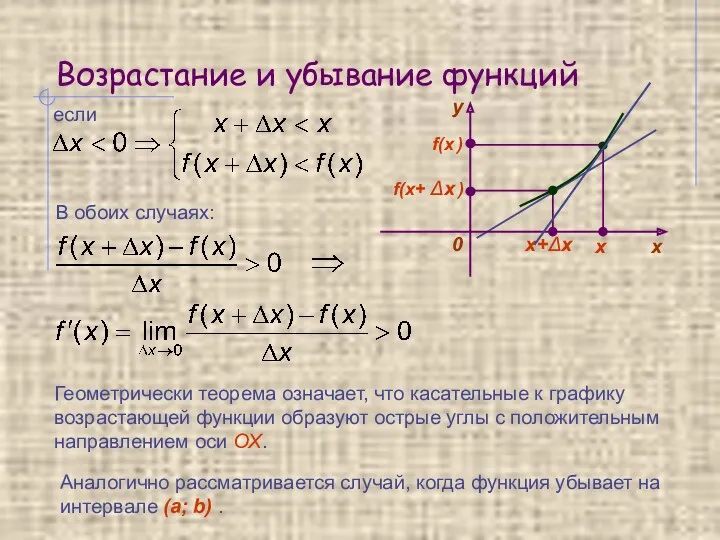
- 3. Возрастание и убывание функций если В обоих случаях: Геометрически теорема означает, что касательные к графику возрастающей
- 4. Возрастание и убывание функций Справедлива также обратная теорема: Если функция дифференцируема на интервале (a; b) и
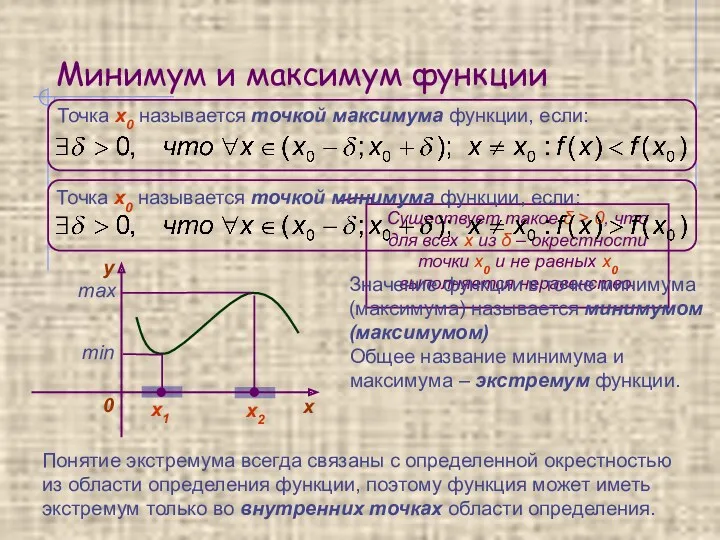
- 5. Минимум и максимум функции Точка х0 называется точкой максимума функции, если: Существует такое δ > 0,
- 6. Минимум и максимум функции Если дифференцируемая функция f(x) имеет экстремум в точке х0, то ее производная
- 7. Минимум и максимум функции Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция:
- 8. Минимум и максимум функции Геометрическая интерпретация доказательства теоремы 4: Правило исследования функции на экстремум. 1 x0
- 9. Минимум и максимум функции Найти экстремум функции Область определения: Критические точки функции: не существует при 0
- 10. Минимум и максимум функции Иногда бывает удобно использовать другой достаточный признак существования экстремума. Теорема 5 (достаточное
- 11. Выпуклость графика функции, точки перегиба График дифференцируемой функции f(x) называется выпуклым вниз (или вогнутым) на интервале
- 12. Выпуклость графика функции, точки перегиба Теорема 6 Теорема 7 (достаточное условие существования точек перегиба) План исследования
- 13. Выпуклость графика функции, точки перегиба Исследовать функцию на выпуклость и найти точки перегиба. Область определения: Критические
- 14. Асимптоты графика функции Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится
- 15. Асимптоты графика функции Если хотя бы один из пределов для нахождения k или b не существует
- 16. Асимптоты графика функции Найти наклонные асимптоты графика функции
- 17. Асимптоты графика функции Прямая x = a является вертикальной асимптотой графика функции y = f(x) ,
- 18. Асимптоты графика функции Найти асимптоты графика функции Область определения функции: - вертикальная асимптота Найдем наклонные асимптоты:
- 19. Общая схема исследования функции и построения графика 1 Нахождение области определения функции f(x); 2 Исследование функции
- 21. Скачать презентацию
















 Время Диск
Время Диск Задачи с практическим содержанием. Задания В1 ЕГЭ по математике
Задачи с практическим содержанием. Задания В1 ЕГЭ по математике Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20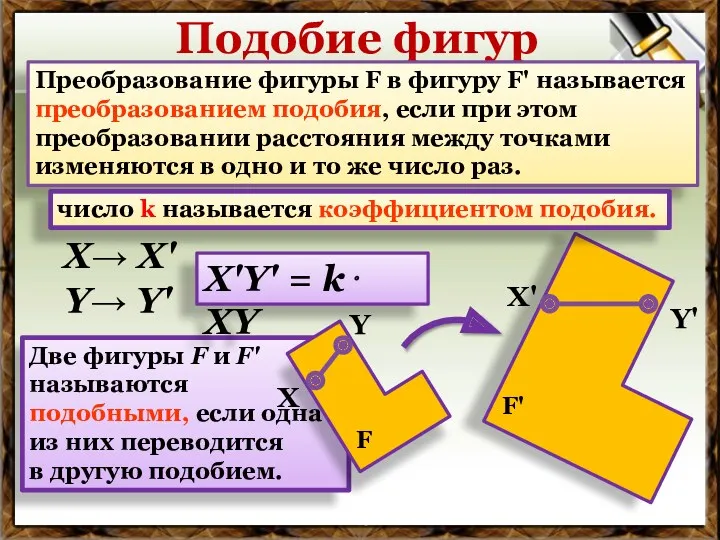 Подобие фигур
Подобие фигур Элементы теории массового обслуживания
Элементы теории массового обслуживания Простейшие тригонометрические уравнения. Решение тригонометрических уравнений
Простейшие тригонометрические уравнения. Решение тригонометрических уравнений Подобные треугольники
Подобные треугольники Тренажёр В гости к Мудрой сове (Математика, 1 класс)
Тренажёр В гости к Мудрой сове (Математика, 1 класс) Тест по теме: Перпендикулярность в пространстве. Теория
Тест по теме: Перпендикулярность в пространстве. Теория Окружность, вписанная в правильный многоугольник
Окружность, вписанная в правильный многоугольник Задания повышенной трудности по математике в начальной школе.
Задания повышенной трудности по математике в начальной школе. Биссектриса угла. 5 класс
Биссектриса угла. 5 класс Элементы статистики и теории вероятностей в курсе математики основной школы. Урок 3. Чтение и построение диаграмм
Элементы статистики и теории вероятностей в курсе математики основной школы. Урок 3. Чтение и построение диаграмм Прямая. Луч. Отрезок. (2 класс)
Прямая. Луч. Отрезок. (2 класс) Тетраэдр. Свойства тетраэдра
Тетраэдр. Свойства тетраэдра Закрепление пройденного материала за 1 полугодие Мультяшки готовятся к Новому году
Закрепление пройденного материала за 1 полугодие Мультяшки готовятся к Новому году Таблица умножения и деления на 2. Игра-тренажер
Таблица умножения и деления на 2. Игра-тренажер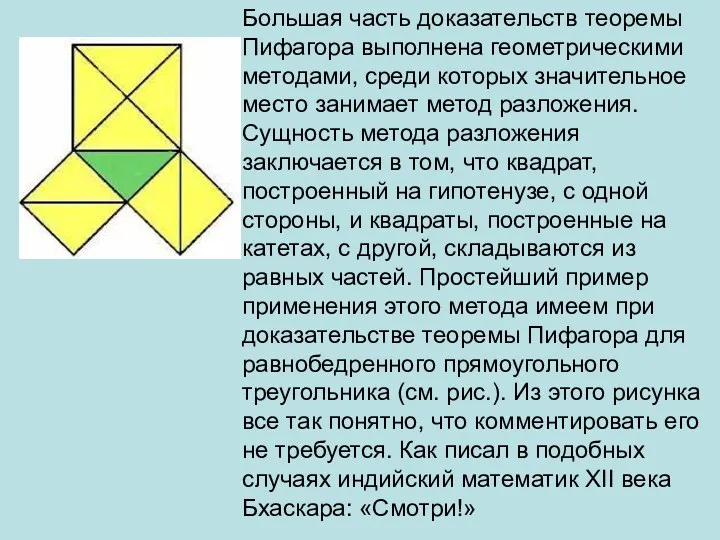 Доказательства теоремы Пифагора
Доказательства теоремы Пифагора Закрепление изученного. Решение задач (4 класс)
Закрепление изученного. Решение задач (4 класс) свойства величин
свойства величин Фрагмент урока. Контрольный тест Числа больше 1000
Фрагмент урока. Контрольный тест Числа больше 1000 Скалярное произведение векторов
Скалярное произведение векторов Задачи, приводящие к понятию определенного интеграла
Задачи, приводящие к понятию определенного интеграла Тренажёр Многозначные числа
Тренажёр Многозначные числа Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланыстар
Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланыстар Математический КВН с учащимися 8-9 классов
Математический КВН с учащимися 8-9 классов Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Презентация Арифметические задачи, 2 класс
Презентация Арифметические задачи, 2 класс