Слайд 2

1. ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕО МТЕРИЯ
Происхождение термина «алгебра»
Название труда арабского
математика
Аль-Хорезми «Аль-джабр-аль-мукабалла»
(Учение о перестановках, отношениях и решениях);
Имя математика Гебера, существование которого, однако, подвергается сомнению.
Слайд 3

Алгебра, как и арифметика и геомерия, - старейший раздел математики
Алгебра вместе
с арифметикой есть наука о числах и через посредство чисел – о величинах вообще. Но арифметика исследует свойства определенных величин, а алгебра – только те свойства величин, которые общи для всех величин независимо от их значений.
Таким образом, алгебра есть обобщенная арифметика, не случайно Исаак Ньютон назвал свой трактат об алгебре «Общая арифметика».
Слайд 4

Алгебру можно определить как науку о количественных соотношениях.
В современном понимании алгебру
можно определить как науку об операциях над любыми математическими объектами.
Слайд 5

Алгебру разделяют на:
Низшую
теория простейших арифметических операциях над алгебраическими выражениями,
решение уравнений
первой и второй степени,
теория степеней и корней,
теория логарифмов,
простейшая комбинаторика;
Слайд 6

Алгебру разделяют на:
Высшую
теория уравнений произвольных степеней,
Теория исключений,
Теория симметрических функций
Теория
подстановок и т.д.
Слайд 7

Линейная алгебра – это раздел высшей алгебры, изучающий объекты линейной природы
(векторные пространства, линейные отображения, системы линейных уравнений).
Среди основных инструментов линейной алгебры – определители, матрицы и т.д.
Аналитическая геометрия – это раздел геометрии изучающий геометрические объек ты средствами алгебры на основе метода координат.
Слайд 8

2. ОСНОВНЫЕ СВЕДЕНИЯ О МАТРИЦАХ
Понятие матрицы и основанный на нем раздел
математики – матричная алгебра – имеют большое значение, так как значительная часть математических моделей экономических, технологических, биологических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
Слайд 9

Матрицей размера m x n называется прямоугольная таблица, содержащая
m строк
и n столбцов.
Числа, составляющие таблицу, называются элементами матрицы.
Элемент, стоящий на пересечении i-ой строки матрицы и её j-го столбца ( i=1,…m j=1,…n) обозначается а ij
Слайд 10

Слайд 11

Слайд 12

Элементы матрицы а ij , у которых i=j, называются диагональными и
образуют главную диагональ матрицы.
Если все недиагональные элементы матрицы равны нулю, то матрица называется диагональной.
Матрица любого порядка называется нулевой или нуль матрицей, если все её элементы равны нулю.
Слайд 13

Слайд 14

3. ОПЕРАЦИИ НАД МАТРИЦАМИ
Над матрицами, как и над числами, можно производить
ряд операций:
1) умножение матрицы на число;
2) сложение матриц;
3) умножение матриц.
Слайд 15

Слайд 16

Произведение любой матрицы А размерности m х n на нуль есть
нулевая матрица, т.е. 0 х А = 0
Общий множитель для всех элементов можно выносить за знак матрицы.
Например:
Слайд 17

Суммой матриц А и В одинакового порядка m х n называется
матрица С того же порядка, элементы которой
Например: сложить матрицы А и В, если:
Слайд 18

Разность двух матриц А и В одинакового порядка mхn определяется через
предыдущие операции: С=А-В=А+(-1)хВ.
Слайд 19

Умножение матрицы А на матрицу В возможно, если число столбцов первой
матрицы равно числу строк второй матрицы.
Произведением матриц Amхn х Bnхk называется такая матрица Cmхk, каждый элемент сij, которой равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В.
Слайд 20

Слайд 21

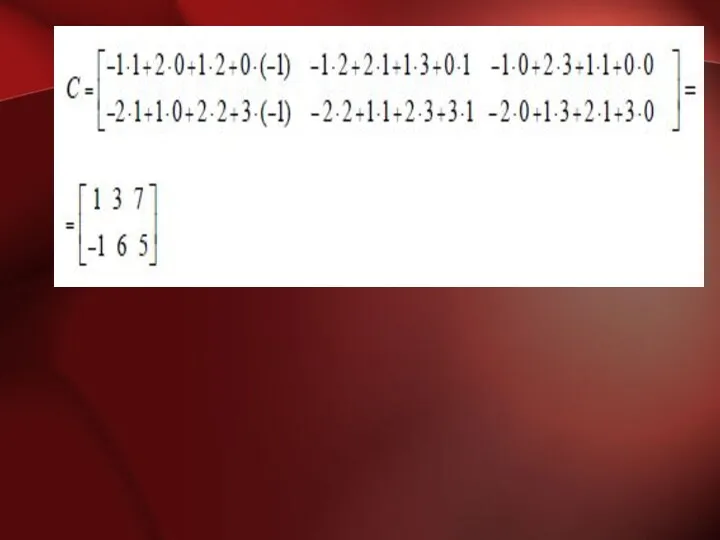
Например: Вычислить произведение матриц Ах В, где
Матрица А имеет размер 2х
4,
матрица В – 4х3.
Найдем размер матрицы произведения:
A2х4 х B4х3 = C2х3
Слайд 22
Слайд 23

Транспонированием матрицы А называется переход к матрице Ат, у которой столбцами
являются строки матрицы А (и наоборот) с сохранением порядка.
Матрица Ат называется транспонированной относительно матрицы А.
Слайд 24

Слайд 25

4. СВОЙСТВА ОПЕРАЦИЙ НАД МАТРИЦАМИ
Слайд 26

Свойства операции транспонирования:
1) (АТ )Т = А
2) (А+ В)Т = АТ
+ ВТ
3) (γхА)Т =γхАТ
4) (А+В)Т =ВТ + АТ
Слайд 27

5. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
Слайд 28

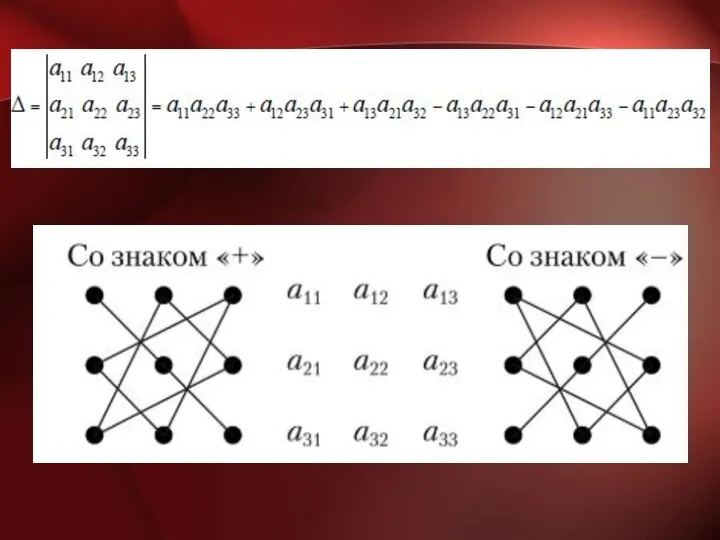
Определителем Δ второго порядка квадратной матрицы А называется выражение:
Слайд 29

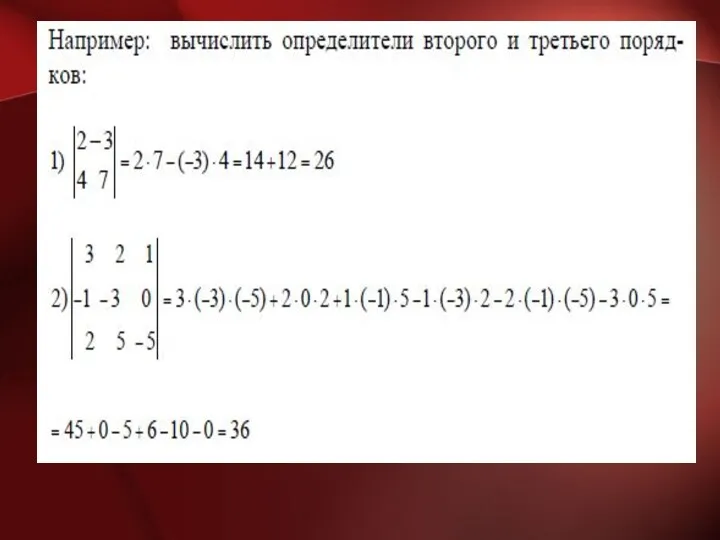
Определитель Δ третьего порядка квадратной матрицы А вычисляется по формуле Саррюса:
Слайд 30
Слайд 31
Слайд 32

6. ОПРЕДЕЛИТЕЛИ N-ГО ПОРЯДКА
Слайд 33

Слайд 34

Слайд 35

Теорема Лапласа
Определитель квадратной матрицы А равен сумме произведений элементов любой строки
(столбца) на их алгебраические дополнения:
разложение определителя по элементам
i-ой строки
разложение определителя по элементам j-го столбца
Слайд 36

Пример. Вычислим определитель матрицы, используя разложение по строке или столбцу:
Разумнее
разложить определитель по элементам 1-ой строки.
Слайд 37

полученные определители третьего порядка можно разложить, например, по первой строке:
Слайд 38

6. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
Если какая-либо строка (столбец) матрицы является нулевой (состоит из
одних нулей), то ее определитель равен нулю.
Если все элементы какой-либо строки (столбца) матрицы умножить на число γ, то ее определитель умножится на число γ.
При транспонировании матрицы ее определитель не меняется:
|А Т| =|А|
При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
Слайд 39

Если матрица содержит два одинаковых ряда, то ее определитель равен нулю
Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраическое дополнение элементов другой строки (столбца) этой матрицы равна нулю, т.е.
Слайд 40

Определитель матрицы не изменится, если к элементам какой- либо строки (столбца)
прибавить элементы другого столбца, умноженные на одно и то же число.
Определитель произведения двух квадратных матриц равен произведению их определителей:
Слайд 41

Слайд 42

Пример. Используя свойства 1-9 определителя, вычислим определитель 4-го порядка:
Слайд 43

7. ПРИВЕДЕНИЕ МАТРИЦЫ К СТУПЕНЧАТОМУ ВИДУ
Слайд 44

Элементарными преобразованиями матрицы являются следующие:
1. отбрасывание нулевой строки (столбца);
2. умножение всех
элементов строки (столбца) матрицы на число ≠ 0;
3. изменение порядка строк (столбцов) матрицы;
4. прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
5. транспонирование матрицы.
Слайд 45

С помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду.
Например:
приведем к ступенчатому виду матрицу А, используя элементарные преобразования, если
Слайд 46

Поменяем местами первую и вторую строки:
Прибавим поэлементно ко 2-ой строке 1-ю
строку, умноженную на (-3),
к 3-ей прибавим 1-ю, умноженную на (-6),
к 4-ой прибавим 1-ю, умноженную на (-2).
Слайд 47

Прибавим к 3-ей строке 2-ю, умноженную на -4,
к 4-ой прибавим
2-ю, умноженную на -5/4;
к 4-ой строке прибавим 3-ю строку, умноженную на -7/20
Получаем ступенчатый искомый вид исходной матрицы
Слайд 48

8. ОБРАТНАЯ МАТРИЦА
Матрица А-1 называется обратной по отношению к квадратной
матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица
А-1 * А = А * А-1 = Е
Слайд 49

Если определитель матрицы А отличен от нуля (|A|≠0), то такая квадратная
матрица называется невырожденной, или неособенной, в противном случае (при |A|=0) - вырожденной или особенной.
Теорема (необходимое и достаточное условие существования обратной матрицы):
Обратная матрица А-1 существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Слайд 50

Обратная матрица находится по алгоритму:
Найти определитель исходной матрицы А.
Если
|A|=0, то матрица А – вырожденная и обратной ей матрицы не существует.
Если |A|≠0, то обратная матрица A-1 существует.
2. Найти матрицу AТ, транспонированную к данной.
3. Найти алгебраические дополнения к каждому элементу транспонированной матрицы.
4. Составить присоединенную матрицу Ã, элементами которой являются найденные алгебраические дополнения.
Слайд 51

5. Вычислить обратную матрицу A-1 по формуле:
6. Проверить правильность вычисления
обратной матрицы, используя равенства:
А-1 * А = А * А-1 = Е
Слайд 52

Пример.
Определить, имеет ли данная матрица обратную, и если имеет, то
вычислить ее. Проверить правильность нахождения обратной матрицы.
Слайд 53

найдем определитель матрицы А:
транспонируем матрицу А:
Слайд 54

3) найдем алгебраические дополнения матрицы
AТ:
Слайд 55

4) составим присоединенную матрицу:
5) Обратная матрица
Слайд 56

6) проверим правильность нахождения A-1:
Слайд 57

9. РАНГ МАТРИЦЫ
Рангом матрицы называется наивысший порядок отличных от нуля
миноров этой матрицы. Ранг матрицы обозначается:
Rang А, или r(A).
Теорема.
Ранг матрицы не изменяется при элементарных преобразованиях.
Слайд 58

Для рангов матриц справедливы следующие соотношения:
Слайд 59

С помощью элементарных преобразований любую (кроме нулевой) матрицу можно привести к
ступенчатому виду, тогда вычисление ранга матрицы не представляет труда.
Слайд 60

Пример. Найти ранг матрицы
Слайд 61

1. Преобразуем матрицу А так, чтобы все элементы какого-либо столбца, например
третьего, кроме элемента а13, обратились в нуль.
Для этого ко второй строке прибавим первую, к третьей – первую, умноженную на (-2), и к четвертой – третью.
Слайд 62

2. Преобразуем теперь матрицу так, чтобы в четвертом столбце все элементы,
кроме элементов первой и второй строк, обратились в нули. Для этого прибавим к четвертой строке вторую, умноженную на (-1), и будем иметь





























































 Время Диск
Время Диск Задачи с практическим содержанием. Задания В1 ЕГЭ по математике
Задачи с практическим содержанием. Задания В1 ЕГЭ по математике Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Подобие фигур
Подобие фигур Элементы теории массового обслуживания
Элементы теории массового обслуживания Простейшие тригонометрические уравнения. Решение тригонометрических уравнений
Простейшие тригонометрические уравнения. Решение тригонометрических уравнений Подобные треугольники
Подобные треугольники Тренажёр В гости к Мудрой сове (Математика, 1 класс)
Тренажёр В гости к Мудрой сове (Математика, 1 класс) Тест по теме: Перпендикулярность в пространстве. Теория
Тест по теме: Перпендикулярность в пространстве. Теория Окружность, вписанная в правильный многоугольник
Окружность, вписанная в правильный многоугольник Задания повышенной трудности по математике в начальной школе.
Задания повышенной трудности по математике в начальной школе. Биссектриса угла. 5 класс
Биссектриса угла. 5 класс Элементы статистики и теории вероятностей в курсе математики основной школы. Урок 3. Чтение и построение диаграмм
Элементы статистики и теории вероятностей в курсе математики основной школы. Урок 3. Чтение и построение диаграмм Прямая. Луч. Отрезок. (2 класс)
Прямая. Луч. Отрезок. (2 класс) Тетраэдр. Свойства тетраэдра
Тетраэдр. Свойства тетраэдра Закрепление пройденного материала за 1 полугодие Мультяшки готовятся к Новому году
Закрепление пройденного материала за 1 полугодие Мультяшки готовятся к Новому году Таблица умножения и деления на 2. Игра-тренажер
Таблица умножения и деления на 2. Игра-тренажер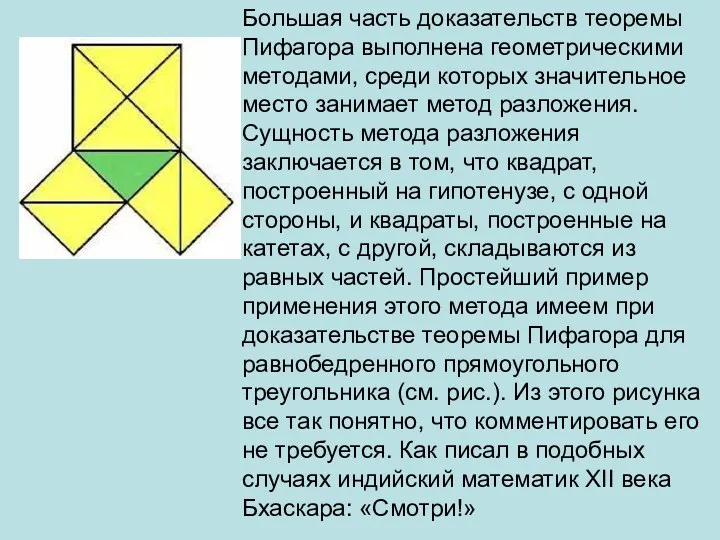 Доказательства теоремы Пифагора
Доказательства теоремы Пифагора Закрепление изученного. Решение задач (4 класс)
Закрепление изученного. Решение задач (4 класс) свойства величин
свойства величин Фрагмент урока. Контрольный тест Числа больше 1000
Фрагмент урока. Контрольный тест Числа больше 1000 Скалярное произведение векторов
Скалярное произведение векторов Задачи, приводящие к понятию определенного интеграла
Задачи, приводящие к понятию определенного интеграла Тренажёр Многозначные числа
Тренажёр Многозначные числа Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланыстар
Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланыстар Математический КВН с учащимися 8-9 классов
Математический КВН с учащимися 8-9 классов Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Презентация Арифметические задачи, 2 класс
Презентация Арифметические задачи, 2 класс