Содержание
- 2. Матрицы
- 3. Матрицей размерности m x n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. где
- 4. Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О.
- 5. Единичная матрица Е – это диагональная матрица, в которой все элементы главной диагонали равны единице, т.е.
- 6. Пример
- 7. Пример
- 8. Пример Вычислить 4А - 3B, если Решение: 4А - 3B = 4А + (-3)B
- 9. 4. Умножение матриц Опр. 17. Произведение матрицы А на матрицу В, определено тогда и только тогда,
- 10. Найти произведение матриц АB и BA Решение: Произведение матриц АB существует, т.к. матрица А имеет размерность
- 11. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
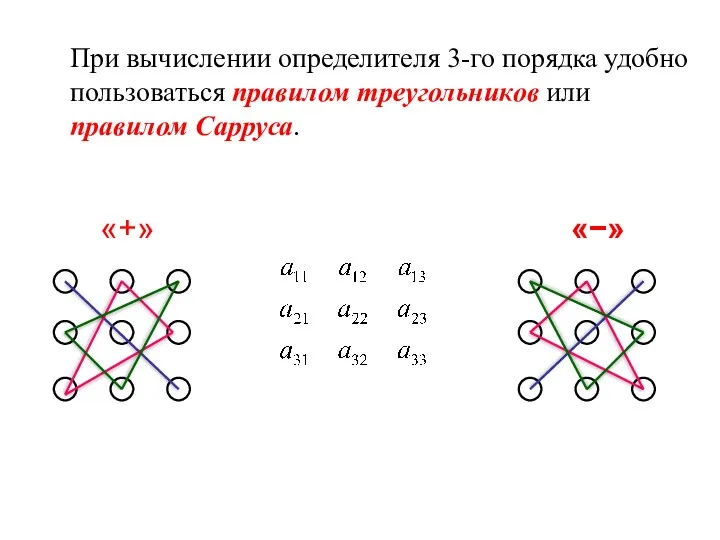
- 12. При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников или правилом Сарруса. «+» «−»
- 13. Пример Вычислить определители матриц:
- 14. Опр.2. Минором элемента aij матрицы n-го порядка A называется определитель матрицы (n-1)-го порядка, полученный из матрицы
- 15. Пример. Найти миноры M11, M32, M43
- 16. Опр.4. Алгебраическим дополнением элемента аij матрицы n-го порядка А называется число, равное (-1)i+jMij и обозначаемое символом
- 17. Определитель n-го порядка матрицы Аn равен сумме произведений элементов любой строки (или столбца) на их соответствующие
- 18. Пример По 2-ой строке:
- 19. Пример По 3-му столбцу:
- 20. Определитель n-го порядка треугольной матрицы равен произведению элементов главной диагонали. Определитель n-го порядка единичной матрицы E
- 21. Ранг матрицы
- 22. Элементарными преобразования матрицы называются : Транспонирование (замена строк столбцами) Перестановка строк и столбцов. Умножение некоторой строки
- 23. Теорема о ранге матрицы
- 24. ОБРАТНАЯ МАТРИЦА
- 25. Опр. 1. Матрица А-1 называется обратной для квадратной матрицы А, если АА-1 = А-1А = Е
- 26. Всякая невырожденная матрица Аn имеет обратную матрицу А-1, причем где Аij – алгебраические дополнения элементов aij
- 27. Пример Найти матрицу, обратную к данной: Решение: Т.к. |А|=-2≠0, то матрица А – невырожденная и имеет
- 28. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 29. Опр. Системой m линейных уравнений с n неизвестными (СЛУ) называется система уравнений где x1, x2, …
- 30. Опр. Матрица А составленная из коэффициентов СЛУ называется основной матрицей системы.
- 31. Опр. Матрицы X и B называются матрицы-столбцы неизвестных и свободных членов.
- 32. Матричная форма записи СЛУ:
- 33. Пример. Записать в матричной форме
- 34. Решение Обозначим Следовательно, имеем AX = B.
- 35. Рассмотрим частный случай неоднородной системы, когда m=n, т.е. систему вида Определитель |А| основной матрицы системы В
- 36. Пример. Решить систему
- 37. Решение. т.е. исходная система трех неоднородных линейных уравнений с тремя неизвестными имеет единственное решение. Найдем единственное
- 39. Следовательно, обратная матрица равна
- 40. Найдем теперь решение системы
- 41. Проверка
- 42. Правило Крамера Согласно правилу Крамера, если |A| ≠ 0, то единственное решение СЛУ вычисляется по следующим
- 43. Найдем теперь решение системы по правилу Крамера
- 44. МЕТОД ГАУССА
- 45. Элементарными называются следующие преобразования системы: Перестановка местами двух уравнений системы. Умножение некоторого уравнения системы на число,
- 47. Скачать презентацию



































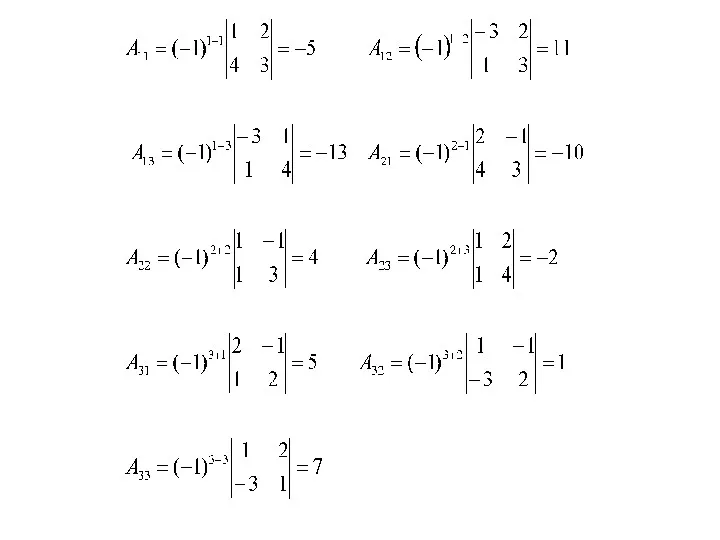







 Сравнение дробей. Устная работа
Сравнение дробей. Устная работа Преобразование произведений тригонометрических функций в суммы
Преобразование произведений тригонометрических функций в суммы Треугольник . Класс коррекции. 7 класс
Треугольник . Класс коррекции. 7 класс Игра Совет мудрейших (часть 2)
Игра Совет мудрейших (часть 2) Геометричні перетворення
Геометричні перетворення Дроби. Сложение и вычитание смешанных чисел
Дроби. Сложение и вычитание смешанных чисел 1 класс. Закрепление. ФГОС
1 класс. Закрепление. ФГОС Анаграммы. Квадратные уравнения
Анаграммы. Квадратные уравнения Умение работать с таблицами и диаграммами, представлять и интерпретировать данные. ВПР по математике. Задание 6
Умение работать с таблицами и диаграммами, представлять и интерпретировать данные. ВПР по математике. Задание 6 Теория вероятностей. Достоверные, невозможные, случайные события
Теория вероятностей. Достоверные, невозможные, случайные события Непрерывность функции
Непрерывность функции Геометрические тела
Геометрические тела Устный счёт в пределах 10
Устный счёт в пределах 10 Число и цифра 0. Сложение и вычитание с числом 0
Число и цифра 0. Сложение и вычитание с числом 0 Введение в биостатистику. Лекция 2
Введение в биостатистику. Лекция 2 Нумерация чисел в пределах 1000
Нумерация чисел в пределах 1000 Прямой счёт
Прямой счёт Длина отрезка
Длина отрезка Одночлен и его стандартный вид
Одночлен и его стандартный вид Основные понятия теории графов
Основные понятия теории графов Какие числа называют обыкновенными дробями?
Какие числа называют обыкновенными дробями? Повторение и закрепление изученного (1 класс)
Повторение и закрепление изученного (1 класс) Қарапайым математикалық түсініктер. Уақытты бағдарлау
Қарапайым математикалық түсініктер. Уақытты бағдарлау Страничка для любознательных. Проверка знаний
Страничка для любознательных. Проверка знаний Статистика – дизайн информации
Статистика – дизайн информации ریاضی چهارم دبستان مبحث :اندازه گیری زمان دبیر :افسانه یوسفی
ریاضی چهارم دبستان مبحث :اندازه گیری زمان دبیر :افسانه یوسفی Математическая статистика. (Лекция 7)
Математическая статистика. (Лекция 7) Справочник по алгебре (7-9 кл.)
Справочник по алгебре (7-9 кл.)