ФУНКЦИЯ - зависимость переменной Y от переменной X.
Обозначается: y = f(x),
где x – независимая переменная или аргумент
Y – зависимая переменная
Область определения функции: все значения, которые принимает X
Область значений функции: все значения, которые принимает Y
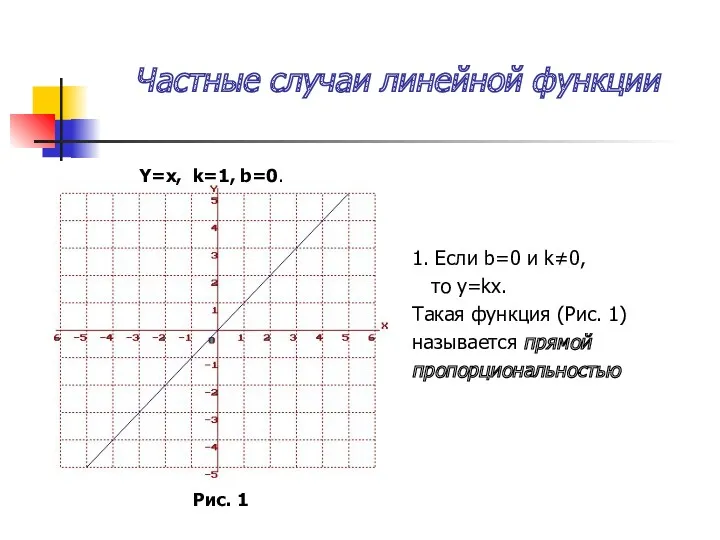
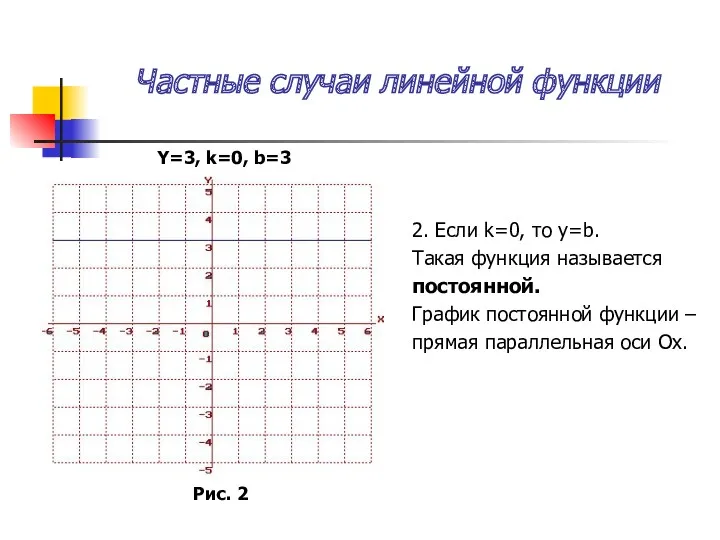
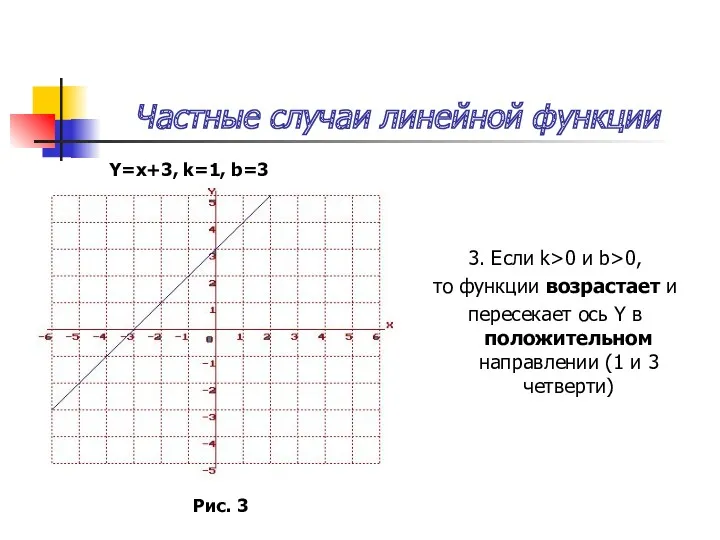
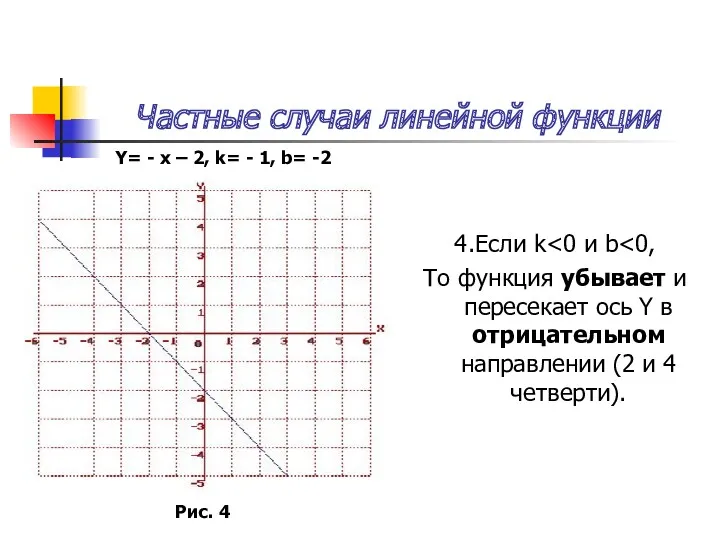
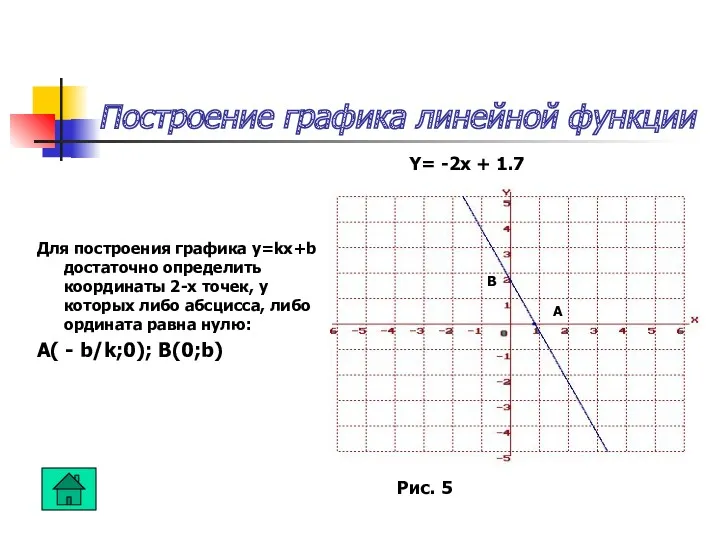
Графиком функции – называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты равны соответствующим значениям функции. Функция представленная в такой форме называется графической моделью, которая описывает конкретный объект или явление.


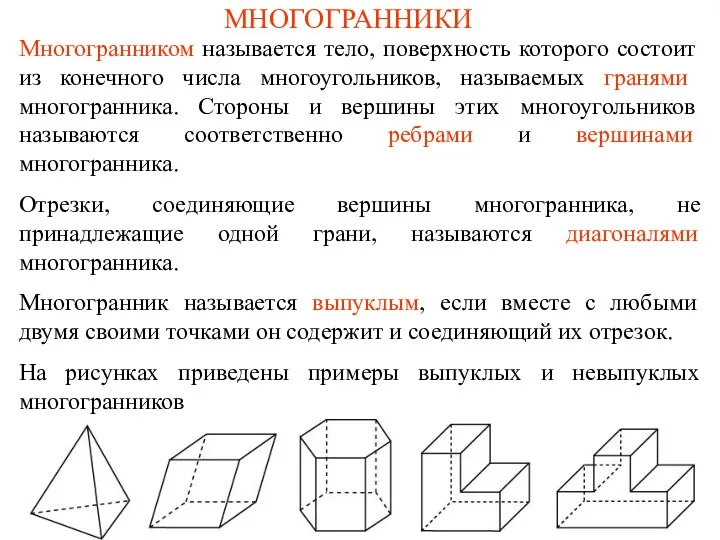 Фигуры в пространстве
Фигуры в пространстве Итоговый тест по математике
Итоговый тест по математике Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции Системы уравнений. Способы решения
Системы уравнений. Способы решения Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Приёмы устных вычислений вида 470 + 80, 560 - 90
Приёмы устных вычислений вида 470 + 80, 560 - 90 Математика в Древнем Египте
Математика в Древнем Египте Устный счет (4 класс)
Устный счет (4 класс) Математическое странствие
Математическое странствие Типы оперирования
Типы оперирования Сложность вычислений
Сложность вычислений Time quiz
Time quiz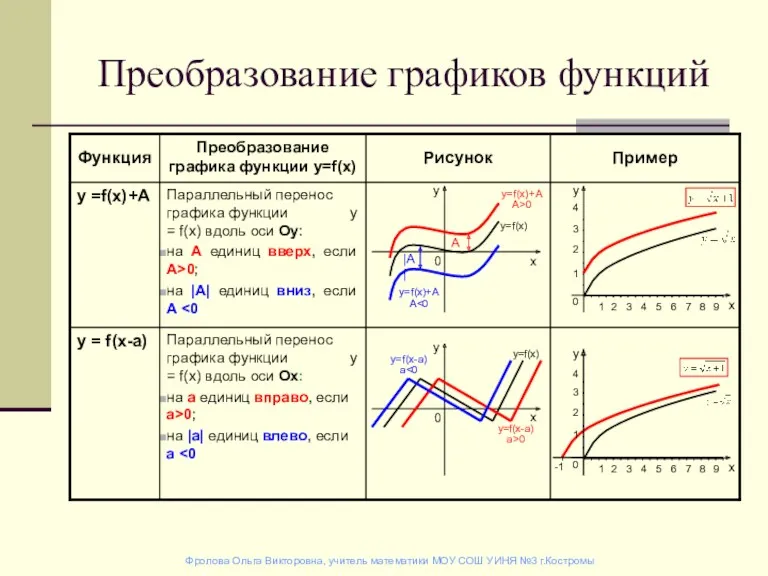 Преобразование графиков функций
Преобразование графиков функций Математика. Решение задач
Математика. Решение задач Описательные статистики
Описательные статистики Сложение и вычитание в пределах 20 (апрель 2014 год).
Сложение и вычитание в пределах 20 (апрель 2014 год). Преобразование графиков функций
Преобразование графиков функций Число и цифра 2.
Число и цифра 2. Интеллектуальный марафон
Интеллектуальный марафон Простые числа. Разложение числа на множители
Простые числа. Разложение числа на множители Решение уравнений и задач с помощью уравнений. 6 класс
Решение уравнений и задач с помощью уравнений. 6 класс Математическая сказка Диск
Математическая сказка Диск Что такое геометрия?
Что такое геометрия? Прямая и обратная пропорциональная зависимости. 6 класс
Прямая и обратная пропорциональная зависимости. 6 класс Применение теории графов к решению задач
Применение теории графов к решению задач Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Сказочная страна функций. Электронный урок
Сказочная страна функций. Электронный урок Введение в Mathlab
Введение в Mathlab