Содержание
- 2. ПОСТАНОВКА ЗАДАЧИ
- 3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)
- 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Параметры регрессии определяются из условия минимума остаточной суммы:
- 5. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (3)
- 7. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 8. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 9. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 10. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ Представим последнее соотношение в эквивалентном виде: где sx, sy - выборочные средние квадратичные отклонения
- 11. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ Обозначив получим r - выборочный коэффициент корреляции Коэффициент корреляции показывает, насколько величин sy в
- 12. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ С учетом (4) получаем: Эта формула обычно используется как определение выборочного коэффициента корреляции Для
- 13. Свойства коэффициента корреляции 1. -1≤r≤1. Чем ближе ⏐r⏐ к 1, тем теснее связь. 2. При r=±1
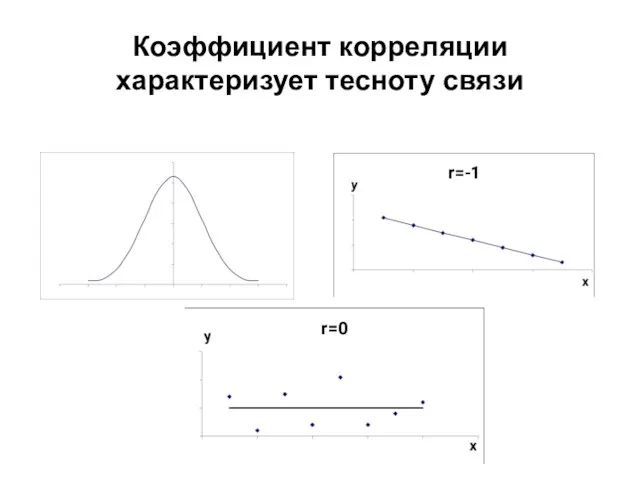
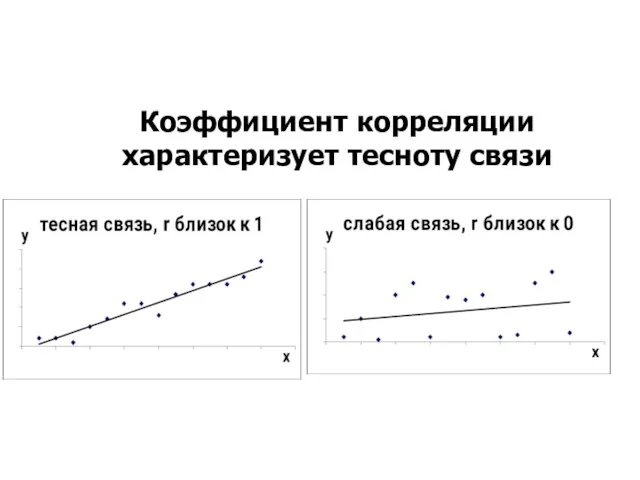
- 14. Коэффициент корреляции характеризует тесноту связи
- 15. Коэффициент корреляции характеризует тесноту связи
- 16. Классическая нормальная линейная регрессионная модель Предположим, что: X - детерминированная величина; ε1, …, εn- независимые нормальные
- 17. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ Для упрощения выкладок можно вместо функции (5) максимизировать ее логарифм (т. к. логарифм
- 18. Свойства оценок: несмещенность МП-оценки могут иметь смещение!
- 19. Свойства оценок: состоятельность для состоятельной несмещенной оценки выполняется закон больших чисел
- 20. Свойства оценок: состоятельность Может использоваться для определения необходимого числа наблюдений, если задано допустимое отклонение оценки от
- 21. Свойства оценок: эффективность
- 22. Несмещенность оценок параметров регрессии формула (3) Доказательство несмещенности параметра m:
- 23. Несмещенность оценок параметров регрессии
- 24. Несмещенность оценок параметров регрессии
- 25. Несмещенность оценок параметров регрессии
- 26. Теорема Гаусса-Маркова В условиях классической нормальной регрессионной модели оценки (3) имеют наименьшую дисперсию в классе всех
- 27. ОЦЕНИВАНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ Число неизвестных параметров (m, b) ?для нормированных наблюдений
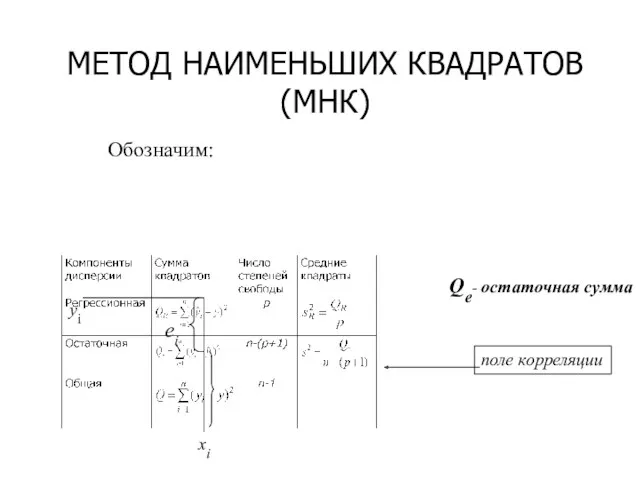
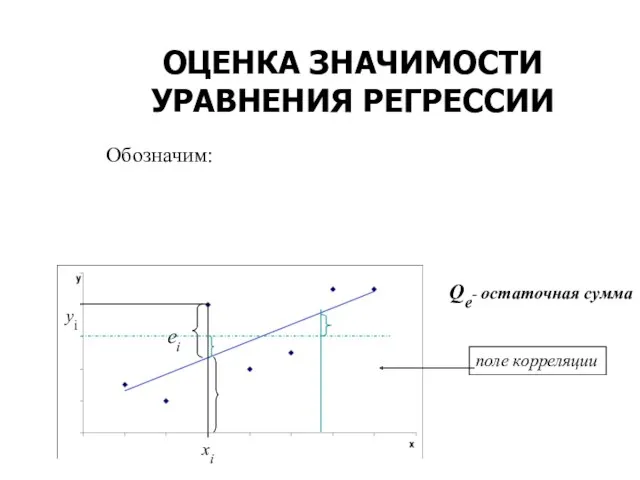
- 28. Обозначим: Qe- остаточная сумма ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
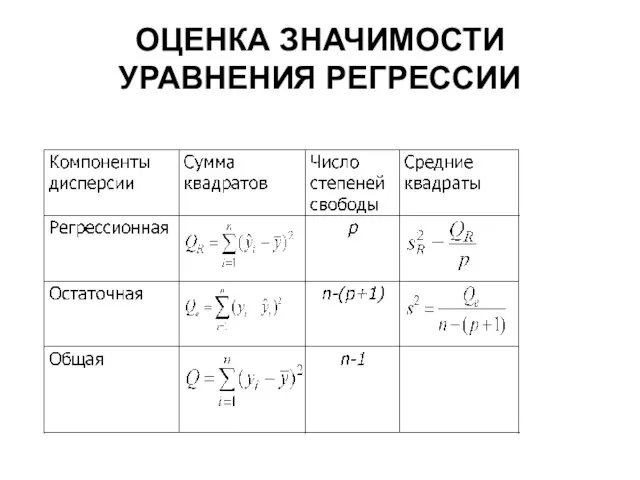
- 29. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 30. Чем меньше остаточная сумма Qe, тем выше качество модели. Чем больше регрессионная сумма QR, тем выше
- 31. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ Можно доказать, что В условиях теоремы Гаусса-Маркова
- 32. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по
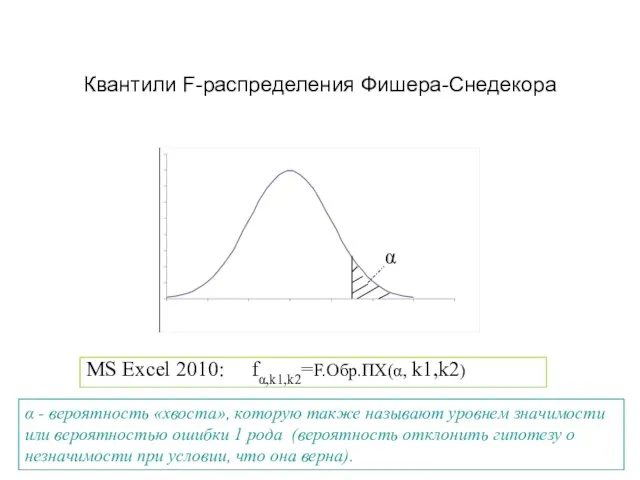
- 33. α Квантили F-распределения Фишера-Снедекора MS Excel 2010: fα,k1,k2=F.Обр.ПХ(α, k1,k2) α - вероятность «хвоста», которую также называют
- 34. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 35. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ Можно доказать, что в случае парной регрессии: R2=r2
- 36. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ QR>Qe – регрессионная модель значима; QR QR=Qe – граничный случай; R2=0.5; R2≥0.5
- 37. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ Критерий (!) проверки гипотезы о незначимости регрессии может использовать значение R2 :
- 38. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ Другой способ оценки значимости уравнения ПАРНОЙ регрессии - проверка гипотезы m=0 если
- 39. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ СКО оценки m не знаем, используем выборочное СКО: -статистика Стьюдента с числом
- 40. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ Для парной регрессии значимость уравнения регрессии эквивалентна значимости коэффициента регрессии Для парной
- 42. Скачать презентацию
































 Задачи на уравнивание
Задачи на уравнивание Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Перпендикуляр и наклонная
Перпендикуляр и наклонная Сумма углов треугольника
Сумма углов треугольника Первый признак равенства треугольников
Первый признак равенства треугольников Теорема синусов. Теорема косинусов. Решение треугольников
Теорема синусов. Теорема косинусов. Решение треугольников Признаки параллельности прямых, 7 класс
Признаки параллельности прямых, 7 класс Решение уравнений
Решение уравнений In elementary algebra, the binomial
In elementary algebra, the binomial Измерение отрезков
Измерение отрезков Разложение квадратного трехчлена на множители
Разложение квадратного трехчлена на множители Игра для учащихся Математический активизатор
Игра для учащихся Математический активизатор Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Нахождение неизвестных компонентов сложения и вычитания многозначных чисел. 8 класс
Нахождение неизвестных компонентов сложения и вычитания многозначных чисел. 8 класс Интегрирование дробно-рациональных функций
Интегрирование дробно-рациональных функций Обыкновенные дроби. Выполните действия
Обыкновенные дроби. Выполните действия Регрессионный анализ
Регрессионный анализ Арифметическая прогрессия
Арифметическая прогрессия Простейшие комбинаторные задачи
Простейшие комбинаторные задачи Векторы. Модуль вектора. Равенство векторов
Векторы. Модуль вектора. Равенство векторов Переместительное свойство сложения 1 класс Диск
Переместительное свойство сложения 1 класс Диск Уравнение окружности (9 класс)
Уравнение окружности (9 класс) Обернена задача
Обернена задача Solução Numérica de Equações Diferenciais
Solução Numérica de Equações Diferenciais Случаи вычитания 16 -
Случаи вычитания 16 - Урок математики в 4 классе. Сквозной урок: математика и сказки Пушкина.
Урок математики в 4 классе. Сквозной урок: математика и сказки Пушкина. Погрешности измерений
Погрешности измерений Описанная сфера
Описанная сфера