Содержание
- 2. Общее уравнение кривой второго порядка К кривым второго порядка относятся: эллипс, частным случаем которого является окружность,
- 3. Окружность Окружностью называется геометрическое место точек на плоскости, равноудаленных от точки А(a; b) на расстояние R.
- 4. Эллипс Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух точек той
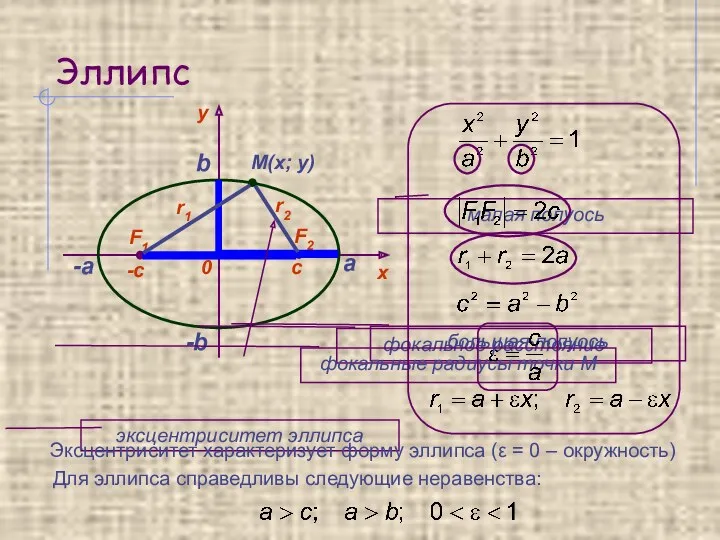
- 5. Эллипс Каноническое уравнение эллипса
- 6. Эллипс а -а b -b Для эллипса справедливы следующие неравенства: Эксцентриситет характеризует форму эллипса (ε =
- 7. Пример Составить уравнение эллипса, фокусы которого лежат в точках F1(-4; 0) F2(4; 0), а эксцентриситет равен
- 8. Гипербола Гиперболой называется геометрическое место точек, разность расстояний от каждой из которых до двух точек той
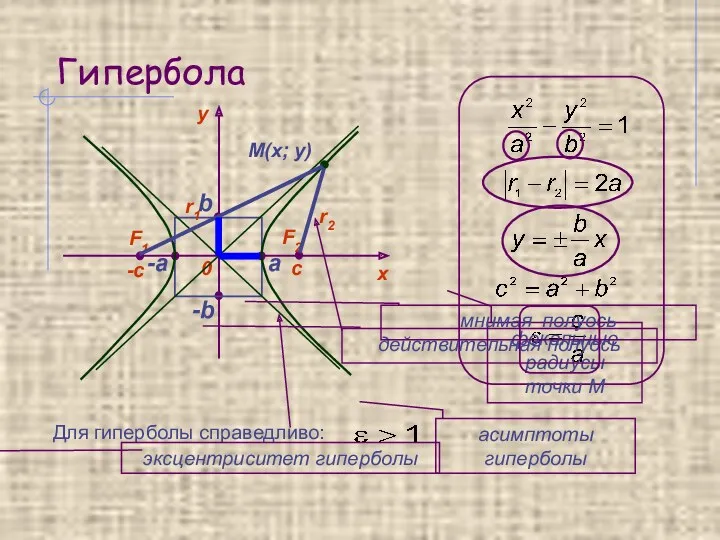
- 9. Гипербола Каноническое уравнение гиперболы После тождественных преобразований уравнение примет вид:
- 10. Гипербола M(x; y) а -а -b b Для гиперболы справедливо:
- 11. Пример Составить уравнение гиперболы, проходящей через точку А(6; -4), если ее асимптоты заданы уравнениями: Решим систему:
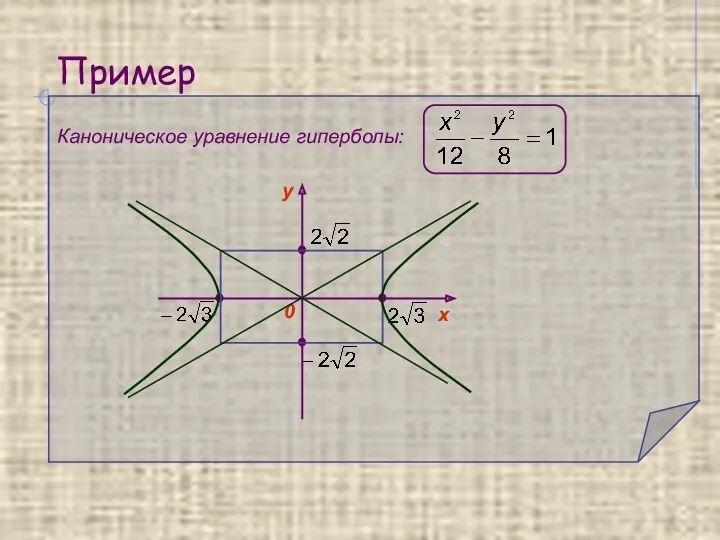
- 12. Пример Каноническое уравнение гиперболы: 0
- 13. Парабола F M(x; y) d r
- 14. Парабола каноническое уравнение параболы фокус параболы Эксцентриситет параболы:
- 15. Преобразование общего уравнения к каноническому виду Составим из коэффициентов уравнения два определителя: Дискриминант старших членов уравнения
- 16. Преобразование общего уравнения к каноническому виду Общее уравнение кривой называется пяти-членным, если 2Bxy=0: Приведение пяти-членного уравнения
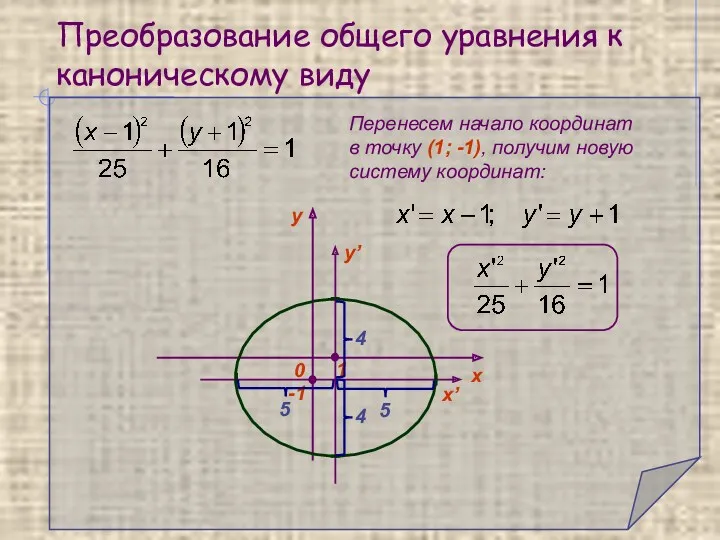
- 17. Преобразование общего уравнения к каноническому виду -1 1 y’ x’ Перенесем начало координат в точку (1;
- 19. Скачать презентацию












 Тренажер. Действия с обыкновенными дробями
Тренажер. Действия с обыкновенными дробями КВН урок математики в 3 классе
КВН урок математики в 3 классе Предмет теории вероятности. Вероятность случайного события
Предмет теории вероятности. Вероятность случайного события Математика в моей жизни. 6 класс
Математика в моей жизни. 6 класс Координатная плоскость
Координатная плоскость Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления
Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления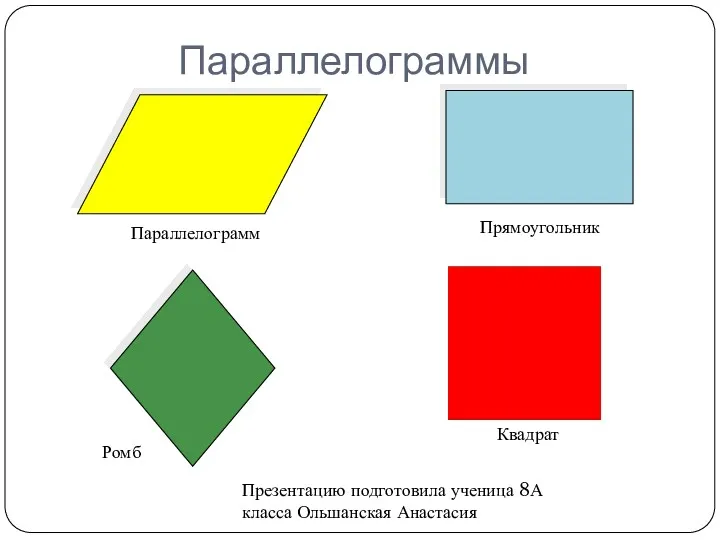 Параллелограммы: ромб, прямоугольник, квадрат
Параллелограммы: ромб, прямоугольник, квадрат Среднее арифметическое
Среднее арифметическое Частные производные функции
Частные производные функции для 4 кл сложение и вычитание многозначн чисел
для 4 кл сложение и вычитание многозначн чисел Метод экспертных оценок
Метод экспертных оценок Свойства степени с натуральным показателем. 7 класс
Свойства степени с натуральным показателем. 7 класс Теорема Пифагора
Теорема Пифагора Образовательная деятельность в разновозрастном детском сообществе ПЧЁЛКА воспитателя Никишкиной Елены Петровны
Образовательная деятельность в разновозрастном детском сообществе ПЧЁЛКА воспитателя Никишкиной Елены Петровны Үшбұрыштардың ұқсастығы
Үшбұрыштардың ұқсастығы Решение неравенств с одной переменной
Решение неравенств с одной переменной Подготовка к контрольной работе
Подготовка к контрольной работе Делители и кратные. 6 класс
Делители и кратные. 6 класс Геометрия. 7 класс
Геометрия. 7 класс Многоугольники. Равные фигуры
Многоугольники. Равные фигуры Правильные многоугольники
Правильные многоугольники Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии Дифференциальные уравнения. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными Основное свойство алгебраической дроби. 8 класс
Основное свойство алгебраической дроби. 8 класс Векторы. Действия над векторами. Проекция вектора
Векторы. Действия над векторами. Проекция вектора Задачи в два действия
Задачи в два действия Радианная мера угла
Радианная мера угла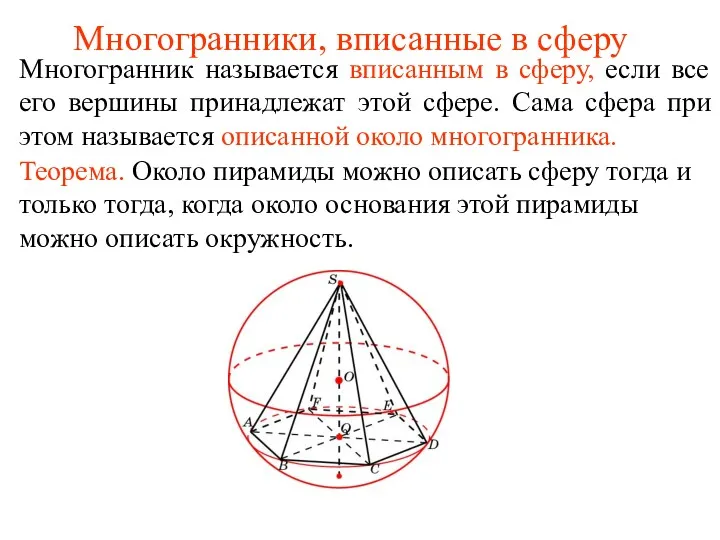 Многогранники, вписанные в сферу
Многогранники, вписанные в сферу