Содержание
- 2. Основные понятия Всякое суждение, утверждающее что-либо о чем-либо, называют высказыванием, если можно сказать, истинно оно или
- 3. Основные понятия Из данных предложений выберите те, которые являются высказываниями: Как пройти в библиотеку? Коля спросил:
- 4. Основные понятия Из данных предложений выберите те, которые являются высказываниями: Здравствуй! Аксиома не требует доказательств. Идёт
- 5. Основные понятия Определите значение логических высказываний: Кислород – газ. Я живу в Москве. Снег - белый.
- 6. Основные понятия Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание называется составным,
- 7. Основные понятия Формализацией высказываний называют операцию замены высказывания естественного языка формулой математического языка, включающего высказывательные переменные
- 8. Логические связки
- 9. Логические связки
- 10. Отрицание Отрицанием (Ā - не А) некоторого высказывания А называется такое высказывание, которое истинно, когда А
- 11. Отрицание Пример 1 Х = "Число 5 является делителем числа 30" __ Х = "Число 5
- 12. Правило построения отрицания к простому высказыванию: При построении отрицания к простому высказыванию либо используется речевой оборот
- 13. Отрицание Задание: Найдите правильно построенное отрицание суждения "Все воздушные шары зелёные": Все воздушные шары не зелёные.
- 14. Конъюнкция Конъюнкция (от латинского conjunctio - союз, связь). Конъюнкцией двух высказываний (А&B - А и В)
- 15. Конъюнкция Пример: А: "У кота есть хвост " В: "У зайца есть хвост" А & B:
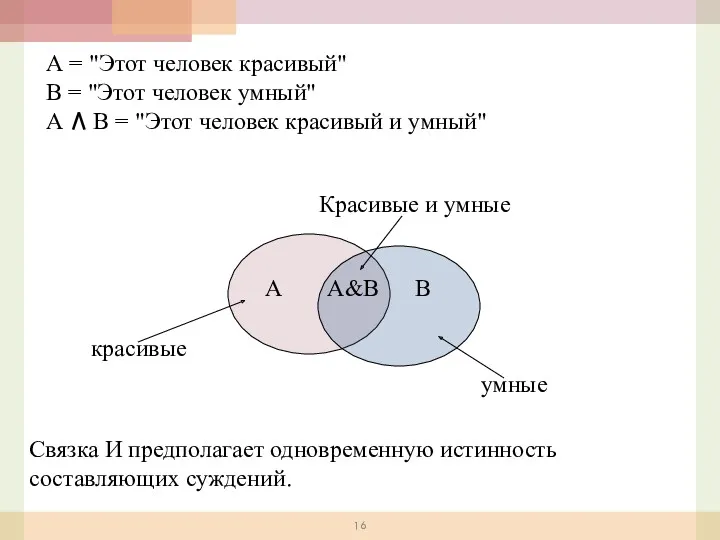
- 16. А = "Этот человек красивый" В = "Этот человек умный" А В = "Этот человек красивый
- 17. Конъюнкция Пример: А = "Черепаха Тортилла жила в пруде 300 лет." В = "Буратино не является
- 18. Дизъюнкция Дизъюнкция (от латинского disjunctio - разобщение, различие). Дизъюнкцией двух высказываний А и В (АVB -
- 19. Дизъюнкция Пример: А: "У кота есть длинный хвост " В: "У зайца есть длинный хвост" А
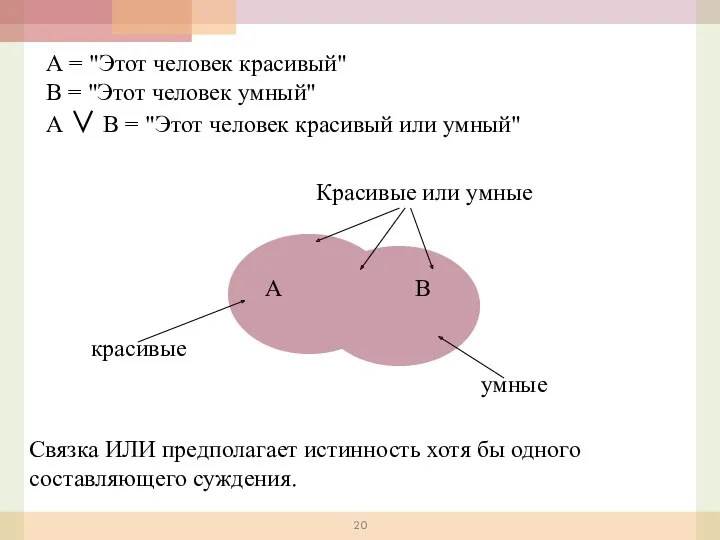
- 20. А = "Этот человек красивый" В = "Этот человек умный" А ∨ В = "Этот человек
- 21. Задания Из двух простых высказываний постройте сложное высказывание, используя логические связки “И”, “ИЛИ” Марина старше Светы.
- 22. Импликация Импликация (от латинского implico - тесно связываю). Импликацией А→В (если А, то В) называется высказывание,
- 23. Импликация Пример: А – «Перевыполню задание» В – «Получу премию» А→В – «Если перевыполню задние, то
- 24. Импликация Примеры: А: «Стало темно» В: «Нужно зажечь свет» А→В: «Если стало темно, то нужно зажечь
- 25. Импликация Пусть А: «Через Смоленск протекает Днепр», В: «Луна сделана из теста». Сформулируйте на обычном языке
- 26. Эквиваленция Эквиваленцией (эквивалентностью) двух высказываний А и В (А~В – А эквивалентно В) называется такое высказывание,
- 27. Эквиваленция Пример. X: данный четырёхугольник – квадрат Y: данный четырёхугольник – прямоугольник X→Y: Если данный четырёхугольник
- 28. Эквиваленция М =«пингвины живут в Антарктиде», К = «3>2», М~К = Людоед голоден тогда и только
- 29. Эквиваленция Пусть S: «Через Смоленск протекает Енисей», C: «2+4=6», N: «2+3=8». Сформулируйте на русском языке высказывания:
- 30. Неравнозначность Неравнозначностью двух высказываний А и В (А⊕В - либо А, либо В) называется такое высказывание,
- 31. Неравнозначность Пример: А: «Сейчас январь» В: «Сейчас июль» А⊕В: «Сейчас либо январь, либо июль». X: «Вася
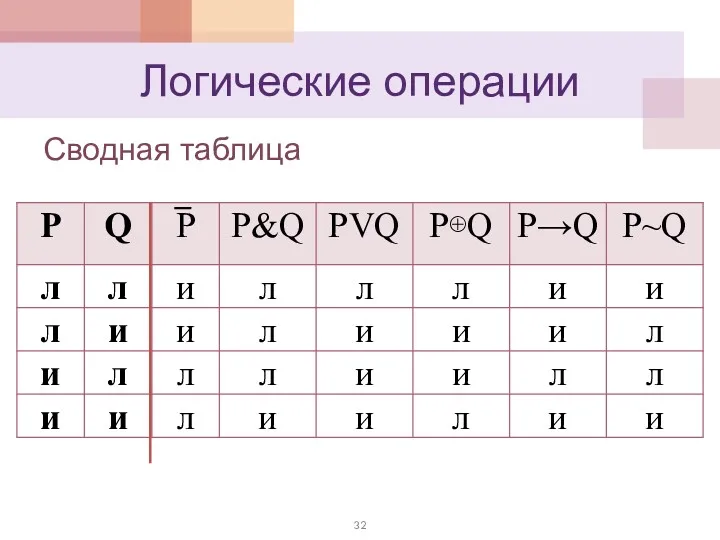
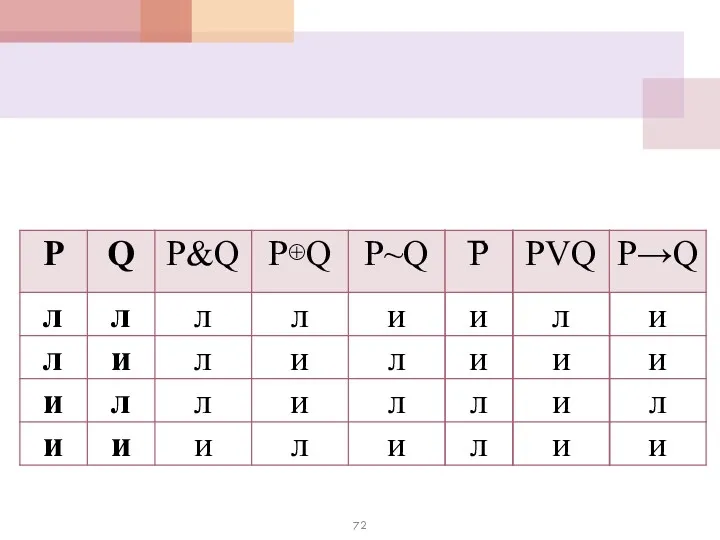
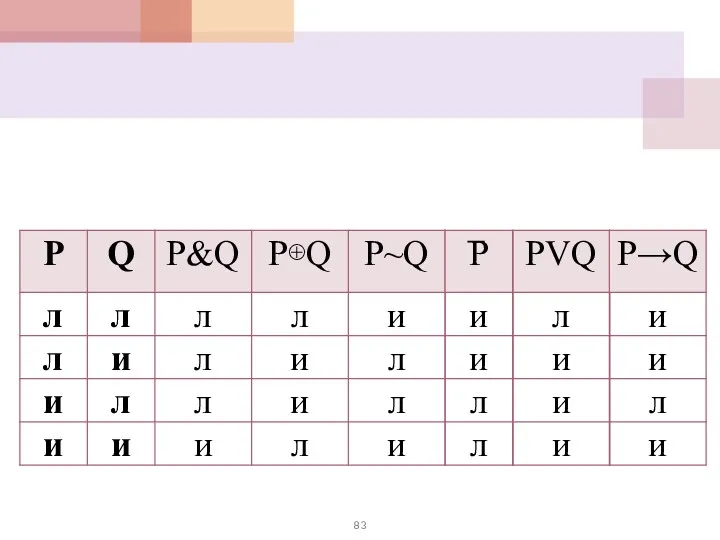
- 32. Логические операции Сводная таблица
- 33. Логические операции Р = {Вася на каникулах поедет в Карелию} Q = {Иван сдаст сессию без
- 34. Логические формулы «Если Сократ — человек и снег — белый, то 7 Разобьем это сложное высказывание
- 35. Логические формулы Итак, символическая запись (X&Y)→Z является своего рода формулой. В формулу (X&Y)→Z вместо переменных X,
- 36. Логические формулы Переменные, вместо которых можно подставлять высказывания, т.е. переменные, пробегающие множество высказываний, называют пропозициональными переменными,
- 37. Логические формулы Определение Каждая отдельно взятая пропозициональная (высказывательная) переменная есть формула алгебры высказываний. Если F1 и
- 38. Логические формулы Определить, какие выражения являются формулами: 1. 2. 3. 4. 5. 6. 7. 8. 9.
- 39. А – «Сегодня понедельник» В – «Сегодня вторник» «Сегодня понедельник или вторник» - (А ⊕ В)
- 40. 3. P – «Идет дождь» Q – «Крыши мокрые» P – «Дождя нет» (P→Q)&(P&Q) 4. А
- 42. 3.
- 43. Тест
- 44. Задания Запишите высказывания в виде логических формул Число 376 четное и трехзначное. Зимой дети катаются на
- 45. Задания Земля имеет форму шара, который из космоса кажется голубым. На уроке математики старшеклассники отвечали на
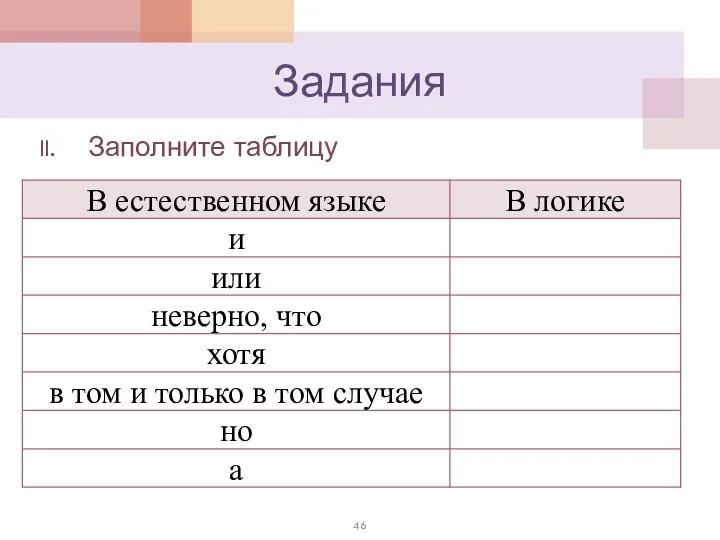
- 46. Задания Заполните таблицу
- 47. Задания Являются ли отрицаниями следующие пары фраз? Он — мой друг. Он — мой враг. Большой
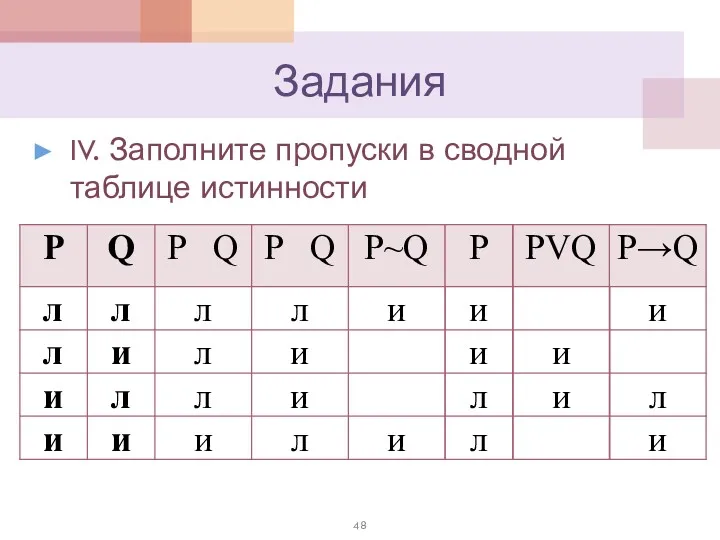
- 48. IV. Заполните пропуски в сводной таблице истинности Задания
- 49. Ответы Запишите высказывания в виде логических операций A&B AVB A⊕B A A→B A&B A&B A→B A~B
- 50. Ответы Заполните таблицу
- 51. Ответы Являются ли отрицаниями следующие пары фраз? Нет Да Нет Нет
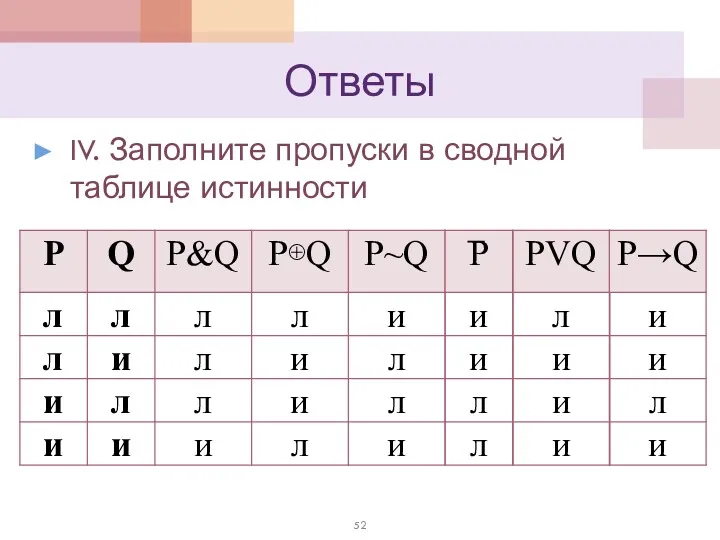
- 52. Ответы IV. Заполните пропуски в сводной таблице истинности
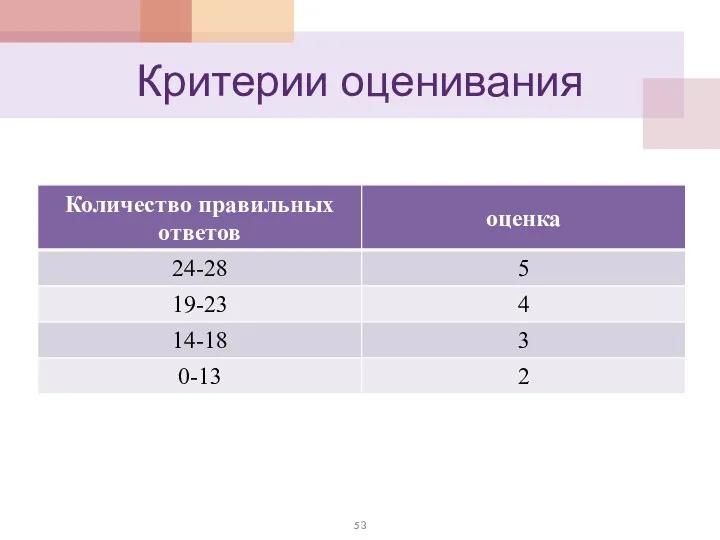
- 53. Критерии оценивания
- 54. Определение истинности сложного высказывания Даны простые высказывания: А = {Принтер – устройство ввода информации}, В =
- 55. Определение истинности сложного высказывания Даны простые высказывания: А = {Принтер – устройство ввода информации}, В =
- 56. Определение истинности сложного высказывания Приоритет логических операций инверсия конъюнкция дизъюнкция импликация и эквивалентность
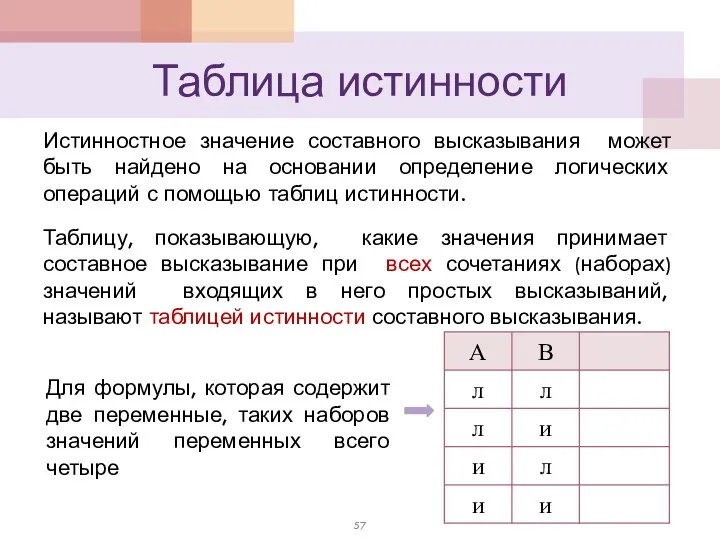
- 57. Таблица истинности Истинностное значение составного высказывания может быть найдено на основании определение логических операций с помощью
- 58. Таблица истинности Если формула содержит три переменные, то возможных наборов значений переменных восемь. В общем случае
- 59. Таблица истинности Алгоритм построения таблицы истинности: Подсчитать количество переменных n в логическом выражении. Определить число строк
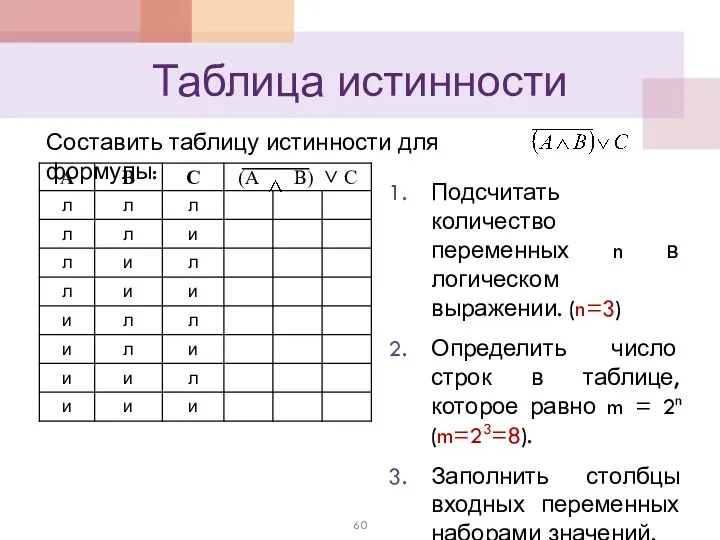
- 60. Таблица истинности Составить таблицу истинности для формулы: Подсчитать количество переменных n в логическом выражении. (n=3) Определить
- 61. Таблица истинности 1 2 3 Определить порядок выполнения логических операций с учетом скобок и приоритетов.
- 62. Таблица истинности 1 1 2 3 Провести заполнение таблицы истинности по столбцам, выполняя логические операции в
- 63. Таблица истинности 1 2 1 2 3 Провести заполнение таблицы истинности по столбцам, выполняя логические операции
- 64. Таблица истинности 1 2 3 1 2 3 Провести заполнение таблицы истинности по столбцам, выполняя логические
- 65. Купят видеокамеру Я начну изучать Photoshop Я начну изучать CorelDraw А ⇒ (В v С) л
- 66. Таблица истинности Составить таблицу истинности для формул:
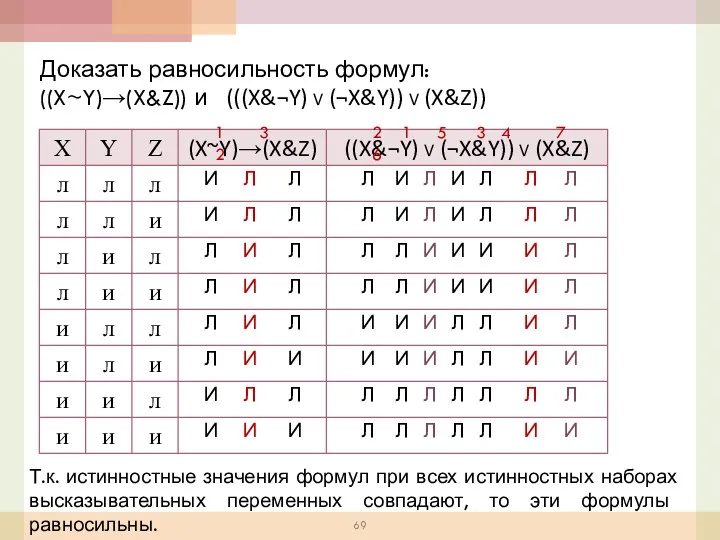
- 67. Равносильные формулы Составим таблицы истинности для формул: и Истинностные значения формул при всех истинностных наборах высказывательных
- 68. Равносильные формулы Формулы называются равносильными, если их значения истинности при любом наборе значений истинности входящих в
- 69. (((X&¬Y) V (¬X&Y)) V (X&Z)) Доказать равносильность формул: ((X~Y)→(X&Z)) и 1 3 2 И И Л
- 70. Определить, являются ли формулы равносильными: ((A&B)⊕C)→B и (A~C) V B X→((X V Y)&(X&Y)) и (X⊕Y) V
- 71. Тавтологии Формулы логики, принимающие значение "истина" при любых значениях истинности входящих в них высказывательных переменных, называются
- 73. Тавтологии Является ли формула тавтологией? Л И И И И Л Л Л И И Л
- 74. ((М⊕Н)& ¬М)→Н ((A→B) & B)→A. Являются ли формулы тавтологиями? 1 3 2 4 Л И И
- 75. Построить таблицу истинности. в Ростове.
- 77. Домашнее задание Записать логической формулой
- 78. Домашнее задание
- 79. Домашнее задание
- 80. Доказать, что формулы являются тавтологиями.
- 81. Законы и теоремы математической логики 1. Ассоциативность & и V (сочетательный закон): а) x1&(x2&x3)=(x1&x2)&x3=x1&x2&x3, б) x1V(x2Vx3)=(x1Vx2)
- 82. 5. Закон двойного отрицания: x = x. 6. Свойства констант 0 и 1: а) x&1=x, б)
- 84. Решение логических задач
- 85. Способы решения ЛЗ С помощью таблиц истинности; Средствами алгебры логики; С помощью рассуждений.
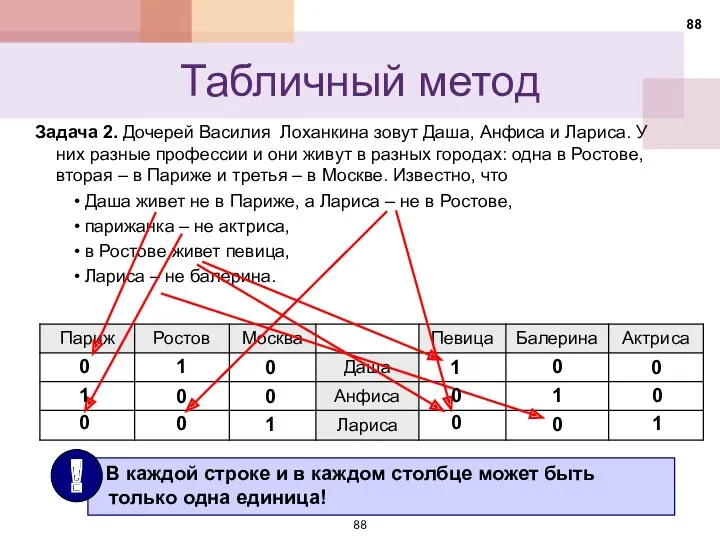
- 86. Табличный метод
- 88. Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии и они
- 89. Задача Эйнштейна Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по
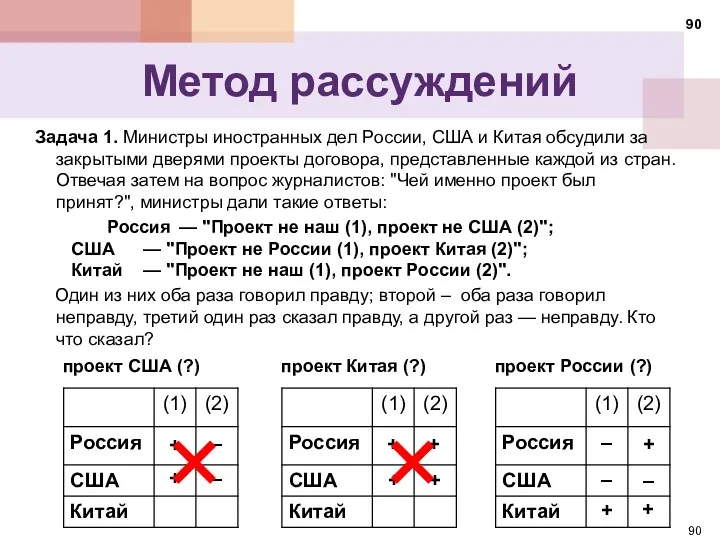
- 90. Метод рассуждений Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты
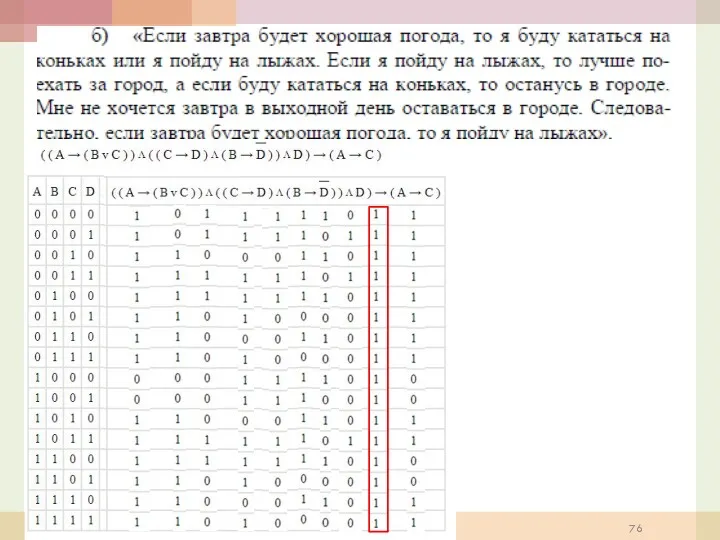
- 91. Задача 1. По телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее: 1.Если не будет
- 92. г) Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия): ( ) ( ) (
- 93. Задача 3. Следующие два высказывания истинны: 1. Неверно, что если корабль A вышел в море, то
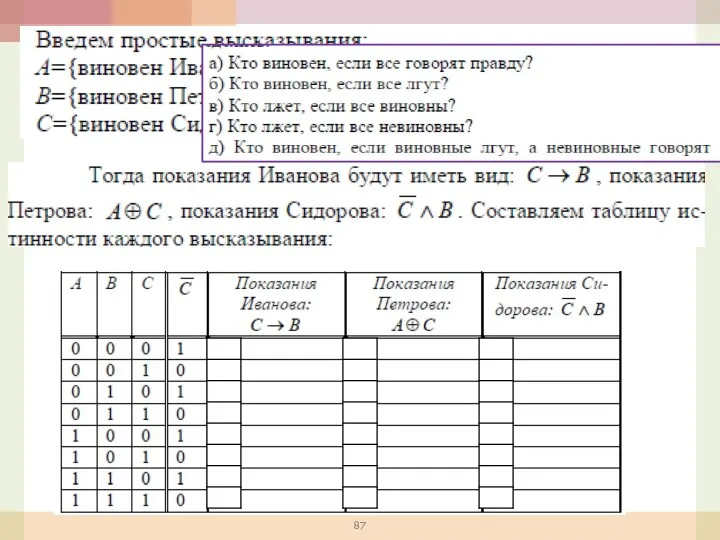
- 94. Пример: Алеша, Боря и Гриша откопали древний сосуд. О том, где и когда он был изготовлен,
- 95. Решение: Введем обозначения простых высказываний: «Это сосуд греческий» – G; «Это сосуд финикийский» – F; «Сосуд
- 96. Т.к. учитель истории сказал ребятам, что каждый из них прав только в одном их двух своих
- 97. Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал
- 98. Использование алгебры логики Задача 4. Когда сломался компьютер, его хозяин сказал «Память не могла выйти из
- 99. Домашняя работа
- 100. Домашняя работа
- 101. Схемы логически правильных рассуждений Логика высказываний
- 102. Умозаключения Рассуждением (умозаключением) называют процесс получения новых знаний, выраженных суждениями (высказываниями), из других знаний, также выраженных
- 103. Правило заключения Правило заключения – утверждающий модус (Modus Ponens) А→В, А В Если из высказывания A
- 104. Правило отрицания Правило отрицания – отрицательный модус (Modus Tollens) А→В, ¬В ¬А Если из A следует
- 105. Правила утверждения-отрицания Правила утверждения-отрицания (Modus Ponendo-Tollens) ((А⊕В)&А)→¬В ((А⊕В)&В)→¬А Пример. "Или я дома, или я вне дома.
- 106. Правила отрицания-утверждения Правила отрицания-утверждения (Modus Tollendo-Ponens) Если истинно или A, или B (в неразделительном смысле) и
- 107. Правила отрицания-утверждения Если истинно или A, или B (в разделительном смысле) и неверно одно из них,
- 108. Правило транзитивности Правило транзитивности (упрощенное правило силлогизма) А→В, В→С А→С Если из A следует B, а
- 109. Правило контрапозиции Правило контрапозиции Если из A следует B, то из того, что неверно B, следует,
- 110. Закон противоречия Закон противоречия А→В, А→¬В ¬А Если из A следует B и ¬B, то неверно
- 111. Примеры неправильных рассуждений а) А→В, В А б) А→В, ¬А ¬В в) АVВ, А ¬В
- 113. 1) 2)
- 114. 3) 4)
- 115. Пример 2. К каким схемам относятся рассуждения:
- 116. Пример 3. Следовательно, она считает ее привлекательной и разворачивает работы по изменению технологии выпускаемого продукта или
- 118. Решение задач 2.
- 120. Скачать презентацию




































































































 Морфологические операции
Морфологические операции Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Задачи на построение. Построение угла
Задачи на построение. Построение угла Решение задач. Треугольники, часть 2
Решение задач. Треугольники, часть 2 Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Решение нелокальных краевых задач для уравнения влагопереноса методами теории случайных процессов
Решение нелокальных краевых задач для уравнения влагопереноса методами теории случайных процессов Решение задач по комбинаторике
Решение задач по комбинаторике Касательная к окружности
Касательная к окружности 12 апреля в истории Кубани. Все действия с десятичными дробями. 5 класс
12 апреля в истории Кубани. Все действия с десятичными дробями. 5 класс Методическая разработка урока математики в 1 классе Однозначные числа
Методическая разработка урока математики в 1 классе Однозначные числа График функции
График функции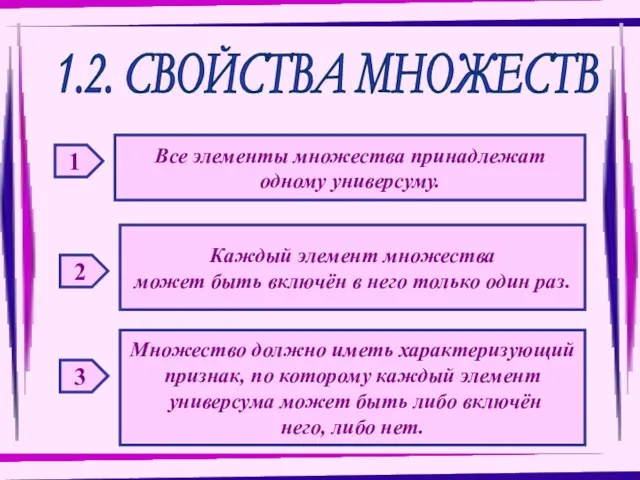 Свойства множеств
Свойства множеств Комплексные числа
Комплексные числа Векторы в пространстве
Векторы в пространстве В помощь 1-м курсам по созданию проекта по математике
В помощь 1-м курсам по созданию проекта по математике Куб
Куб Туынды. Алғашқы функция. Интеграл
Туынды. Алғашқы функция. Интеграл Параллельные прямые
Параллельные прямые Таблица умножения. Интерактивный тренажёр
Таблица умножения. Интерактивный тренажёр Произведение синусов и косинусов
Произведение синусов и косинусов Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs
Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs Деление десятичных дробей. 5 класс
Деление десятичных дробей. 5 класс Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Все действия с натуральными числами. Урок-путешествие к острову натуральных чисел
Все действия с натуральными числами. Урок-путешествие к острову натуральных чисел Деление (математика, 3 класс, УМК Гармония)
Деление (математика, 3 класс, УМК Гармония) Формирование элементарных математических способностей. Для детей 2-3 лет
Формирование элементарных математических способностей. Для детей 2-3 лет Вычитание чисел. 6 класс
Вычитание чисел. 6 класс Көбейту және бөлуді пысықтау
Көбейту және бөлуді пысықтау