Слайд 2

Слайд 3

1. Высшая математика. Практикум ч.2.
Шуман Г.И., Волгина О.А., Голодная Н.Ю.,
Одияко
Н.Н.
2. Высшая математика. Практикум ч.3.
Шуман Г.И., Волгина О.А.
3. Высшая математика. Практикум ч.4.
Шуман Г.И., Волгина О.А.
Слайд 4

Дифференциальное исчисление функции одной переменной (производная).
Задача, приводящая к понятию производной.
2.
Определение производной.
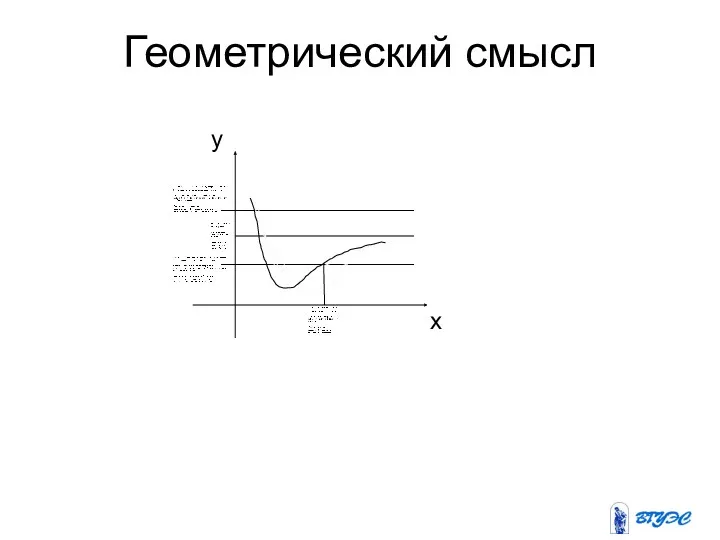
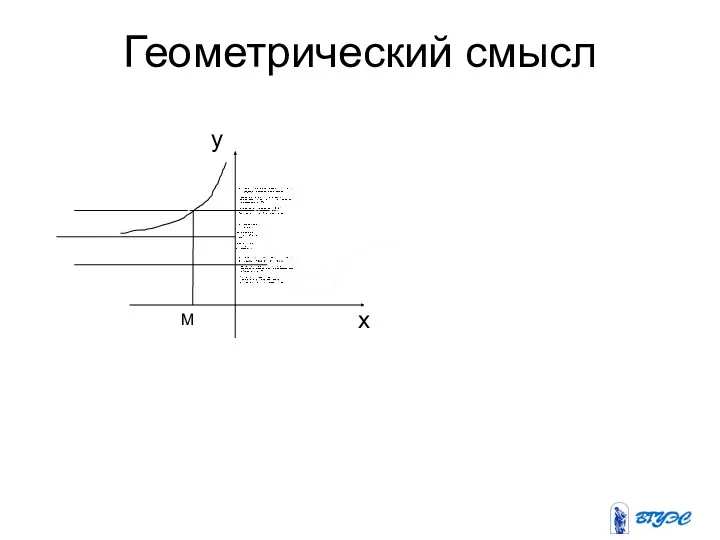
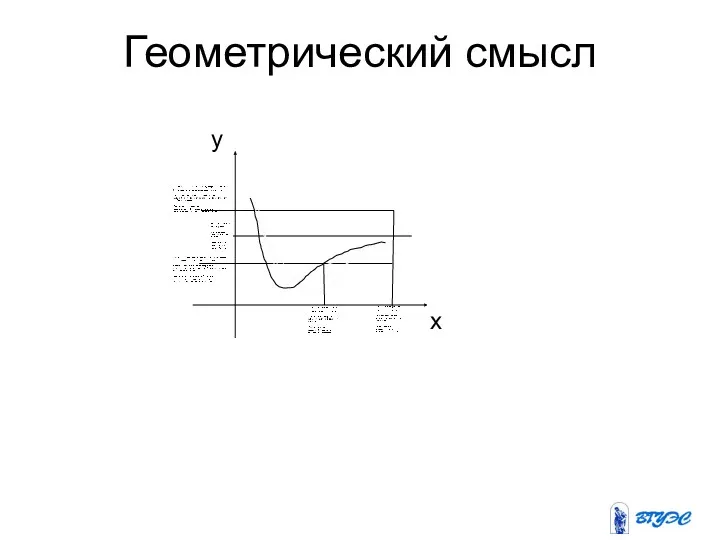
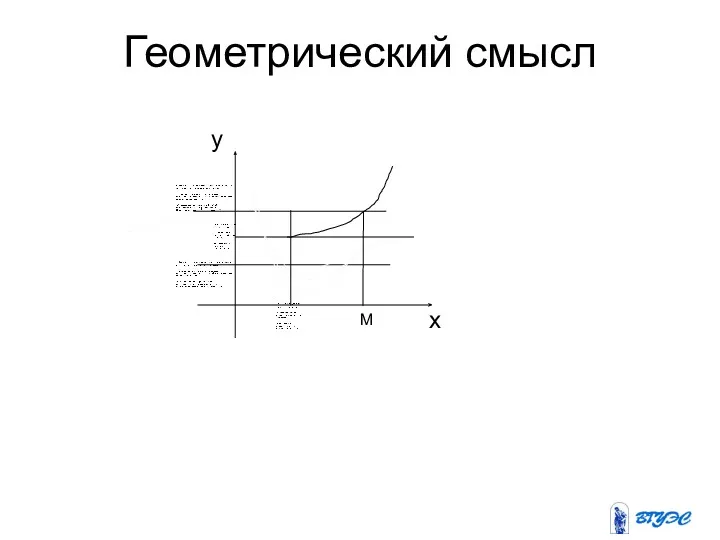
3. Геометрический смысл производной.
4. Основные правила дифференцирования.
5. Производные основных элементарных
функций.
Слайд 5

Слайд 6

Функцией называется правило, по
которому каждому элементу некоторого
множества М соответствует
единственный
элемент другого множества N.
- независимая переменная (аргумент);
- зависимая переменная;
М - область определения функции;
N - множество значений функции.
Слайд 7

Графиком функции наз.
множество точек плоскости , для
каждой из которых
абсцисса
является значением аргумента, а
ордината - соответствующее значение
данной функции.
Слайд 8

Способы задания функции:
аналитический;
2) табличный;
3) графический.
Слайд 9

Основные элементарные функции
Слайд 10

Постоянная .
Степенная
Показательная
Слайд 11

Логарифмическая
Тригонометрические
Обратные тригонометрические
Слайд 12

Окрестностью точки числовой
прямой называется любой интервал
содержащий эту точку (
Слайд 13

точки
числовой прямой называется
интервал ,т.е. если ,
то или
Слайд 14

Слайд 15

-произвольное множество.
Ограниченное сверху:
Ограниченное снизу:
Ограниченное:
Слайд 16

Слайд 17

Слайд 18
Слайд 19

Слайд 20
Слайд 21

Слайд 22
Слайд 23

Слайд 24
Слайд 25

Слайд 26

Слайд 27
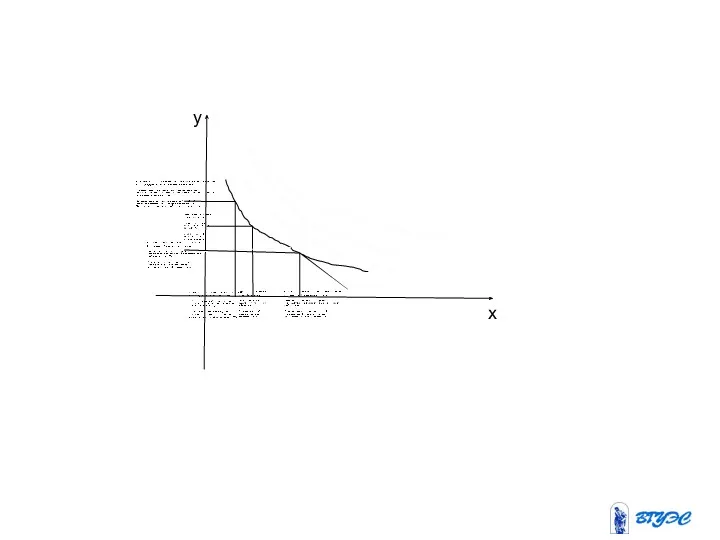
Слайд 28
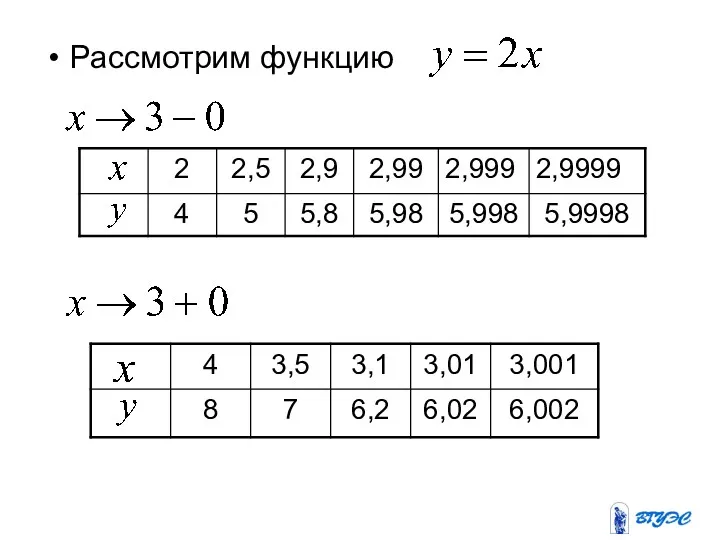
Слайд 29
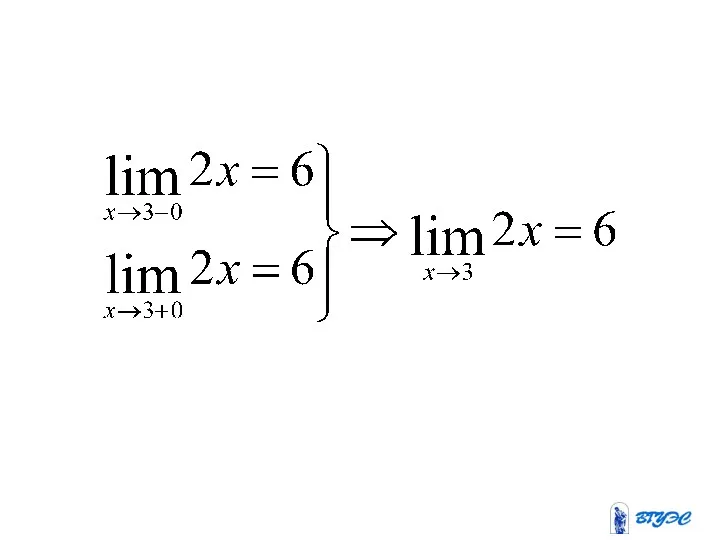
Слайд 30

Слайд 31

Слайд 32

Свойства бесконечно малых функций
Слайд 33

Слайд 34

Бесконечно большие функции
Слайд 35

Теорема. Если бесконечно малая
при и , то
бесконечно большая при
Теорема.
Если бесконечно
большая функция при , то
бесконечно малая при
Слайд 36

Слайд 37

Слайд 38
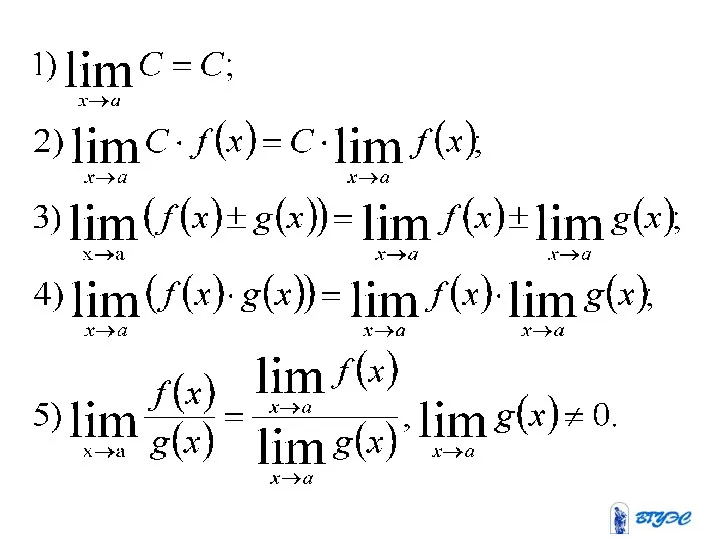
Слайд 39
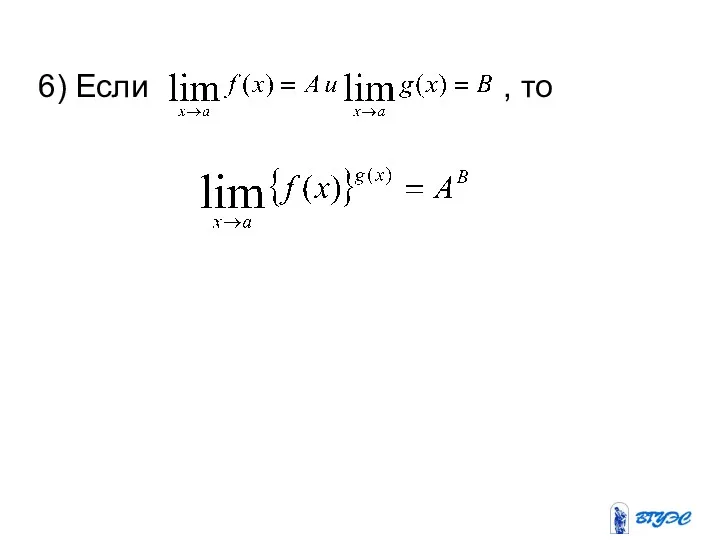
Слайд 40

Теорема о зажатой переменной
Слайд 41

Первый замечательный предел
Слайд 42
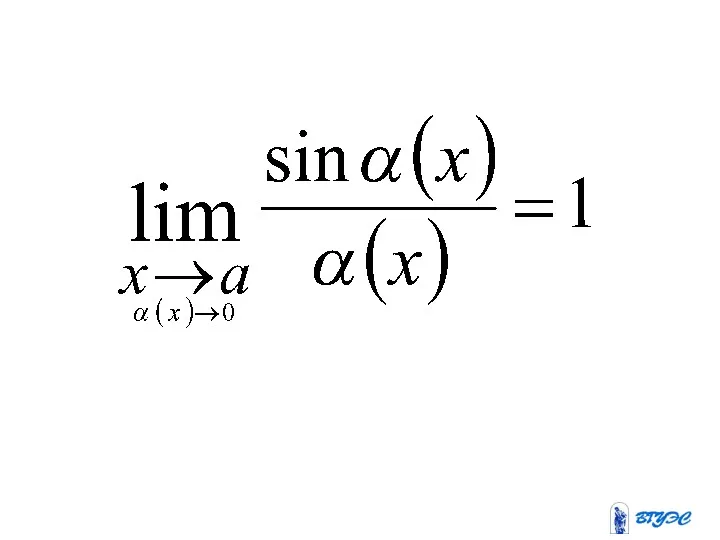
Слайд 43

Доказательство проведем для частного случая , т.е. докажем, что
.
Неопределенность
, свойство о пределе частного не применимо.
Слайд 44
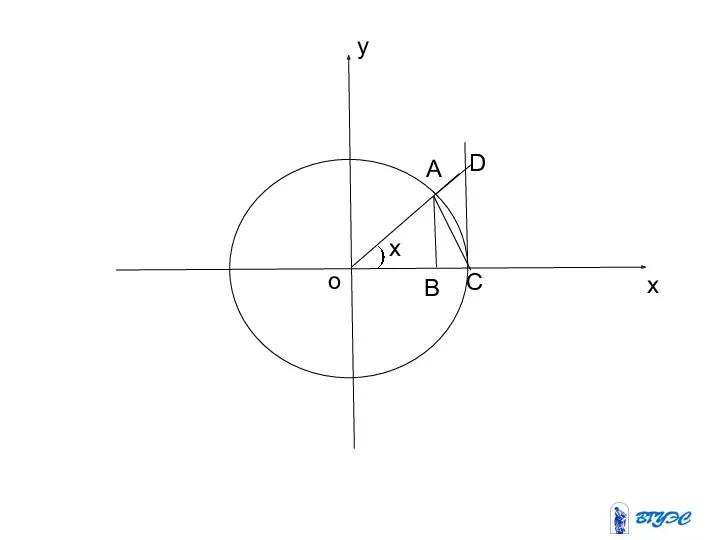
Слайд 45
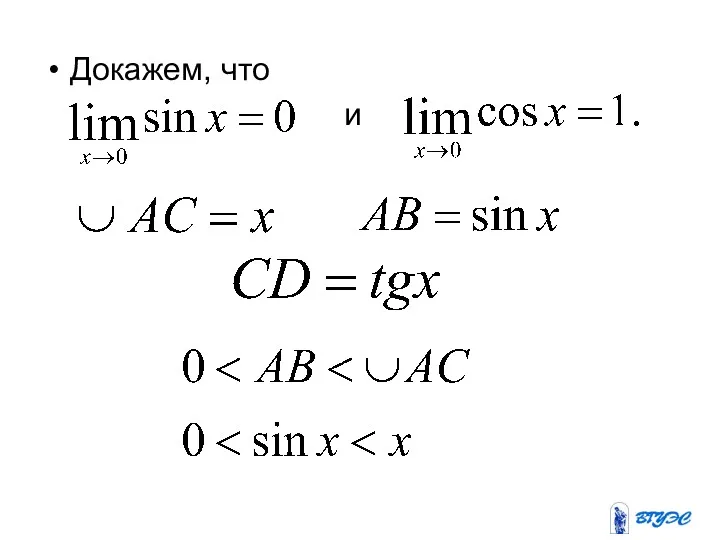
Слайд 46
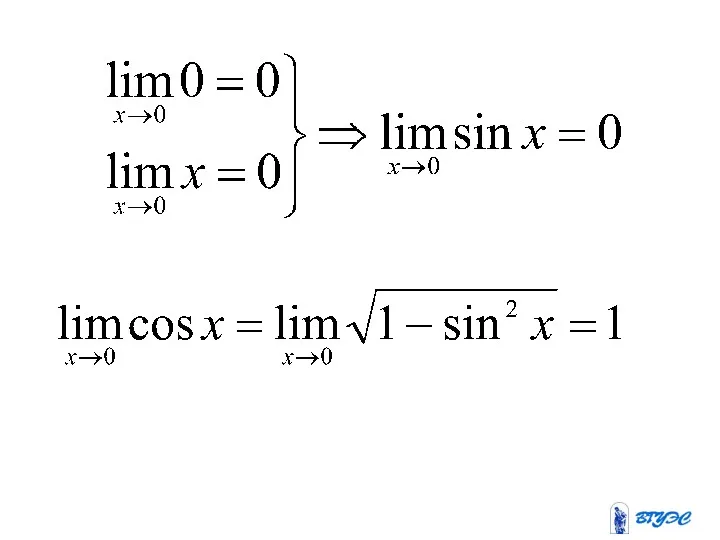
Слайд 47
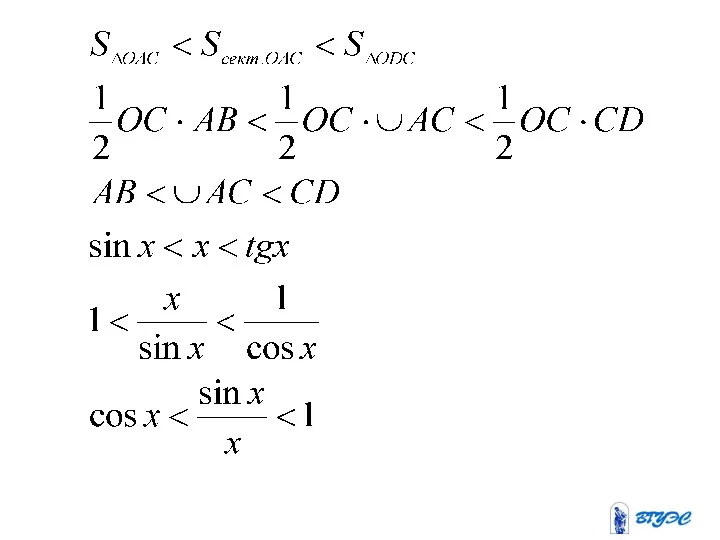
Слайд 48
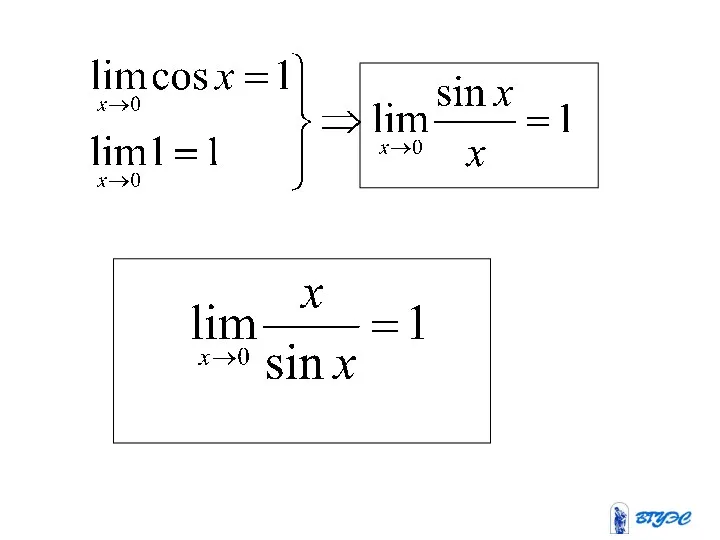
Слайд 49
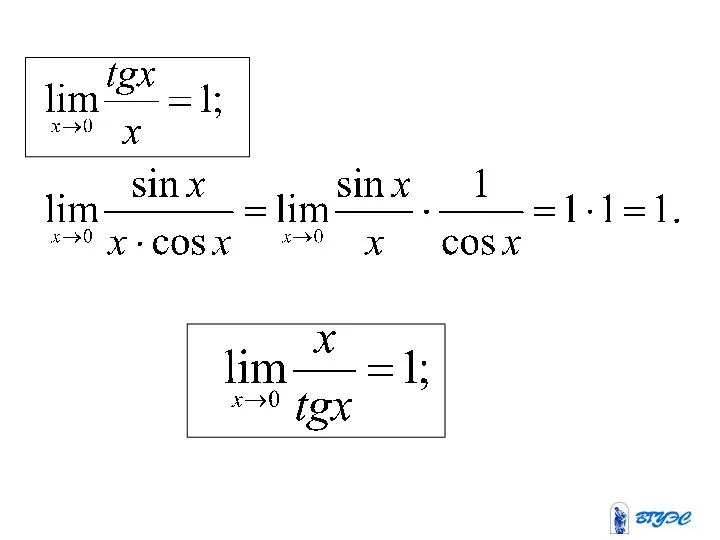
Слайд 50
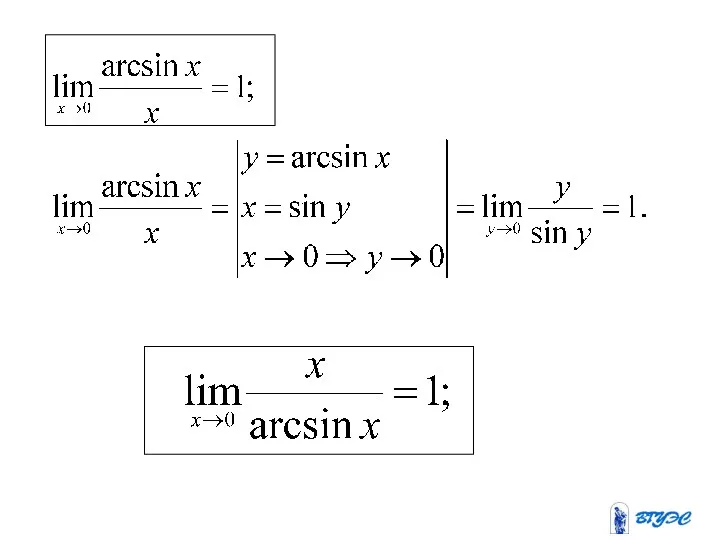
Слайд 51
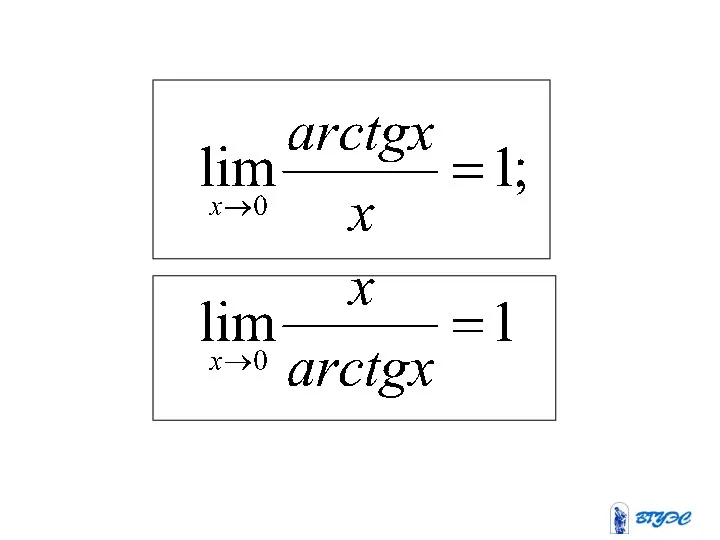
Слайд 52
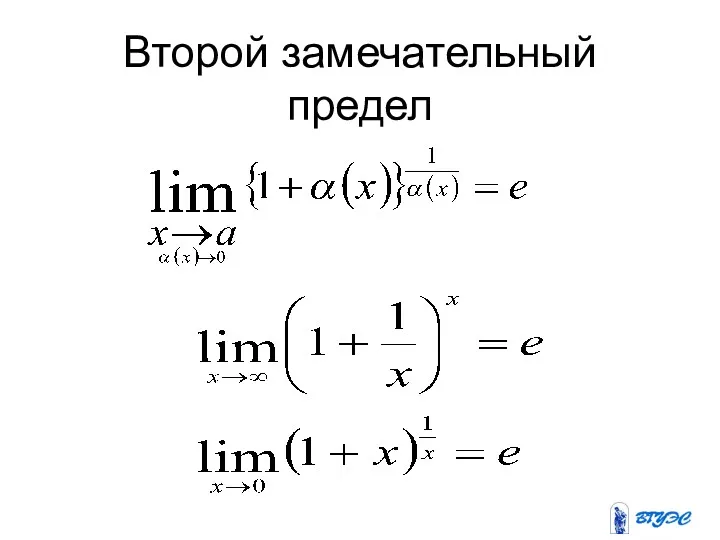
Второй замечательный предел
Слайд 53
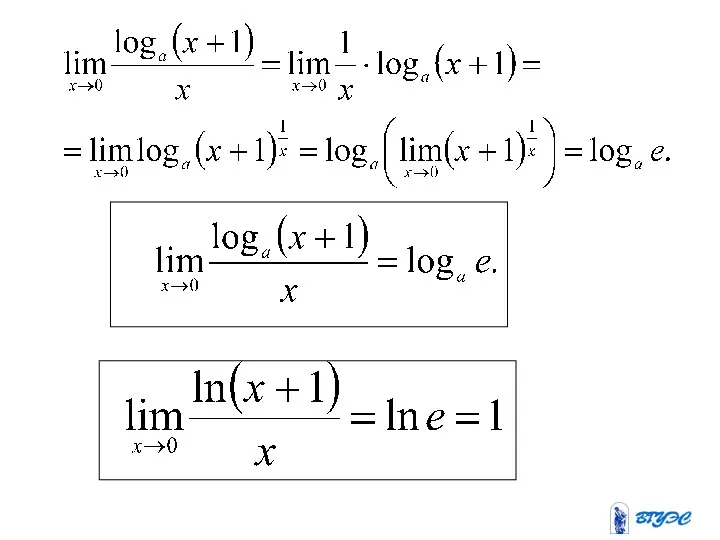
Слайд 54

Слайд 55

Сравнение бесконечно малых
Слайд 56

Пусть и бесконечно малые
функции при :
1) и называются б.м.
одного
порядка малости при , если
существует конечный
Слайд 57

2) бесконечно малые и одного
порядка малости при называются
эквивалентными бесконечно
малыми,
если
Слайд 58

Слайд 59

3) бесконечно малая называется
бесконечно малой более высокого
порядка чем бесконечно
малая при
, если
Слайд 60

4) если не существует конечного
то и называются
несравнимыми бесконечно малыми при
Слайд 61

Теорема. Пусть и
бесконечно малые функции при (а
конечно и бесконечно)
и существует
, тогда существует
Слайд 62
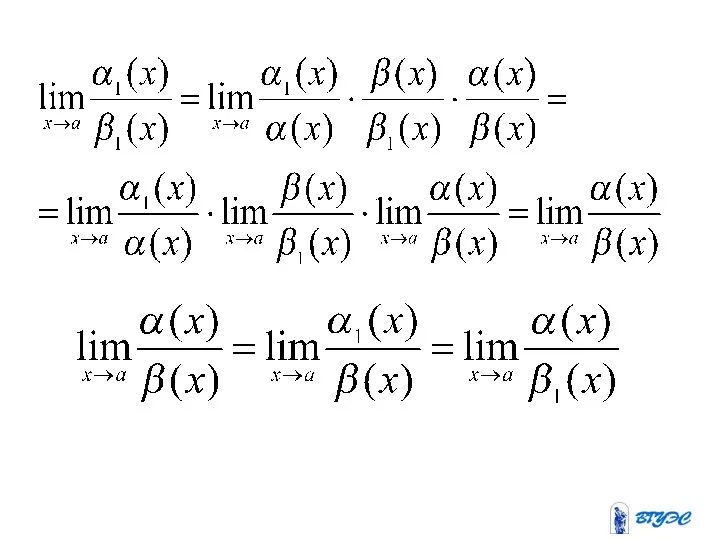
Слайд 63

Слайд 64

Слайд 65

Слайд 66

Слайд 67

Функция наз. непрерывной в
точке , если:
функция определена в точке и
некоторой её окрестности;
2) существует
3)
Слайд 68

Классификация точек разрыва
Слайд 69

Точка, в которой нарушается
непрерывность функции, называется
точкой разрыва этой функции.
Точка
разрыва функции
называется точкой разрыва первого рода,
если существуют конечные пределы
Слайд 70

Если хотя бы один из односторонних
пределов не существует или равен
бесконечности, то точка называется
точкой разрыва второго рода.
Точка разрыва называется точкой
устранимого разрыва функции , если
Слайд 71

Пусть - точка разрыва первого рода
функции . Скачком функции в
точке называется
Слайд 72

Свойства функций непрерывных в точке
Слайд 73

Слайд 74

Функция называется
непрерывной на отрезке , если она
определена на этом
отрезке, непрерывна
в каждой точке интервала , а на
концах отрезка непрерывна соответственно
слева и справа, т.е.
Слайд 75

Свойства функций непрерывных на отрезке
Слайд 76

1.Если функция непрерывна
на отрезке , то она достигает на
этом
отрезке своего наибольшего и
наименьшего значений.
Следствие. Если функция
непрерывна на отрезке , то она
ограничена на этом отрезке.
Слайд 77

2.Если функция непрерывна
на отрезке и на его концах
принимает значения
разных знаков, то
внутри отрезка существует по
крайне мере одна точка, в которой
значение функции равно нулю.
Слайд 78

3. Пусть функция непрерывна
на и
Тогда для любого числа ,заключенного
между и , найдется точка ,
такая, что
Слайд 79

Пусть дана функция .
Рассмотрим два значения её аргумента:
Исходное и
новое .
Разность наз.приращением
аргумента в точке и обозначим :
Слайд 80
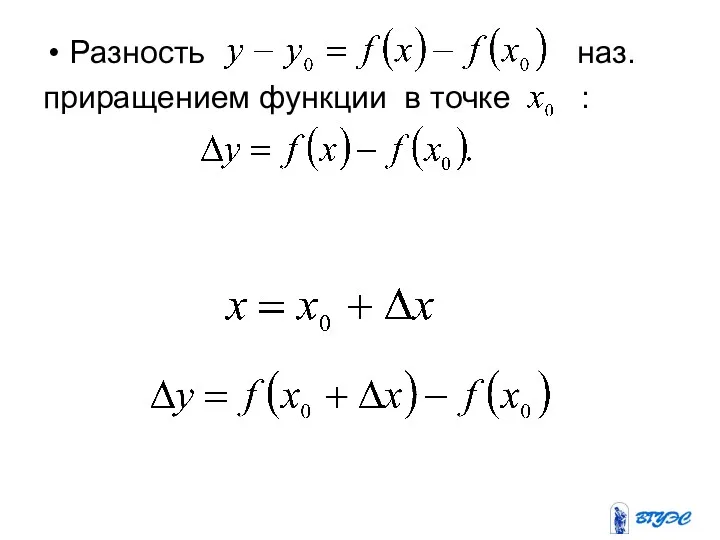
Разность наз.
приращением функции в точке :
Слайд 81





































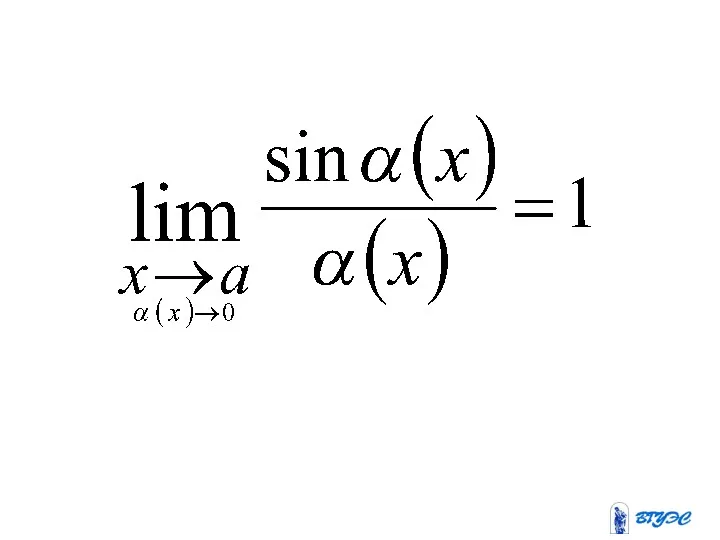


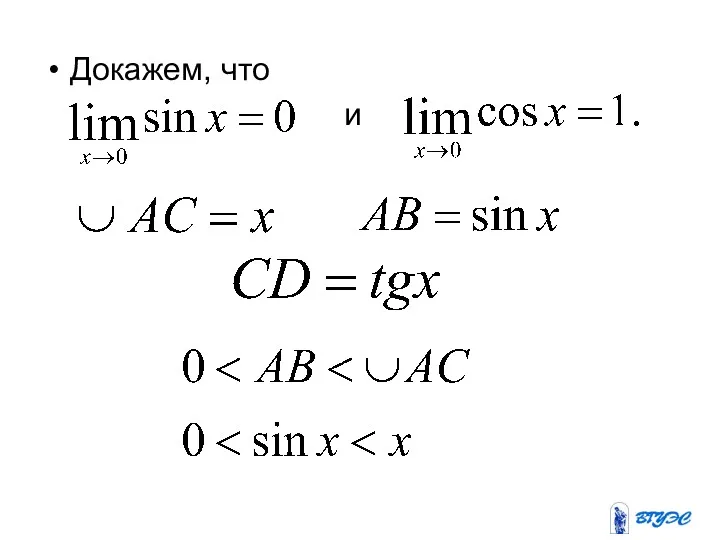
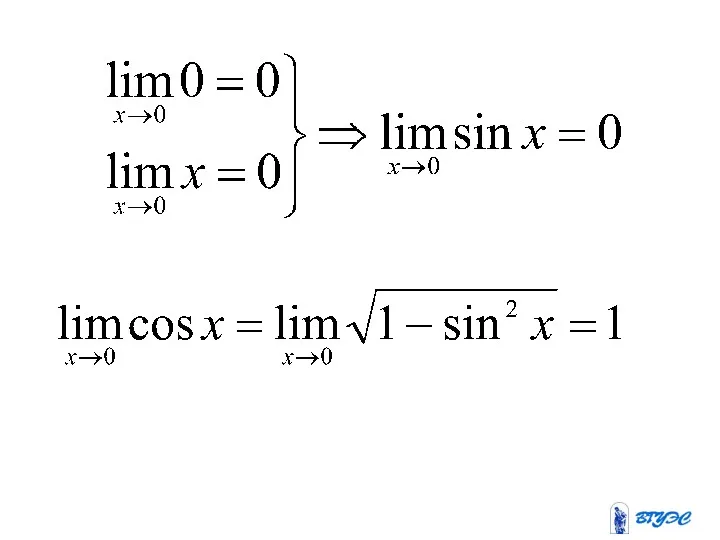
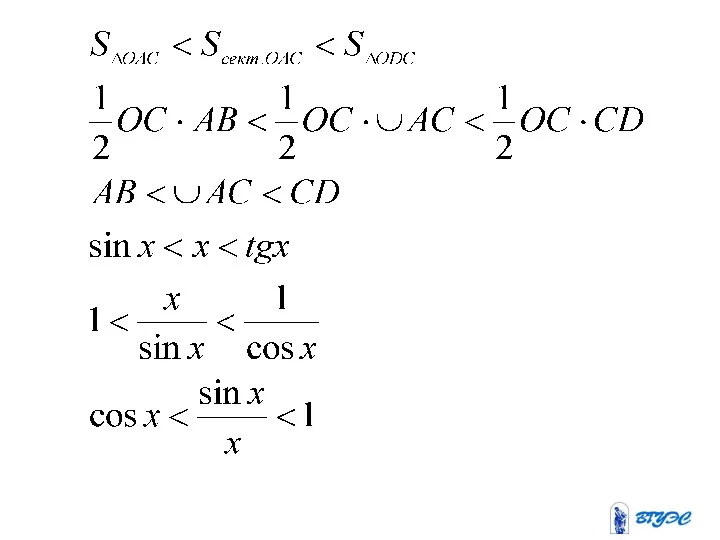
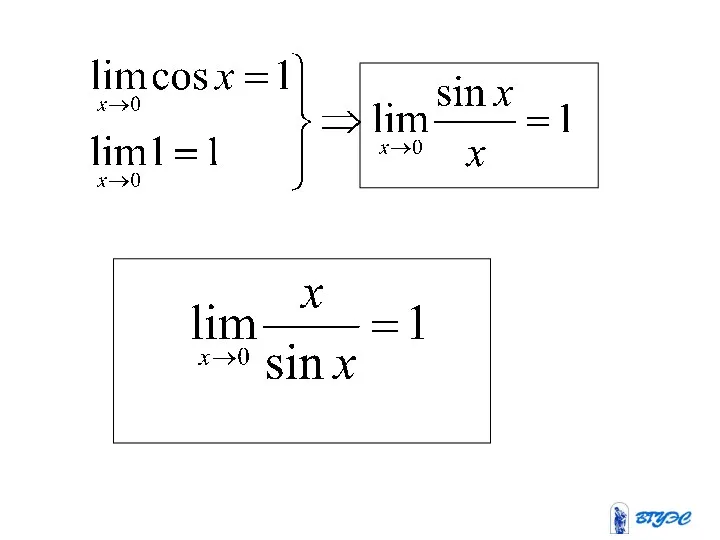
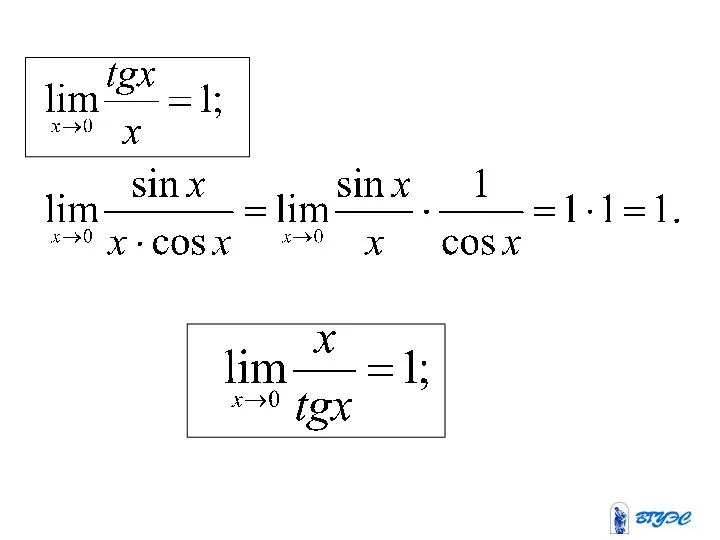

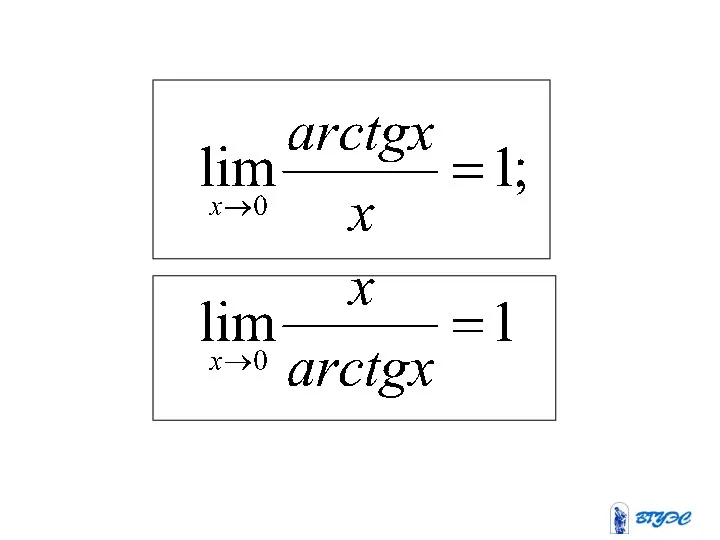
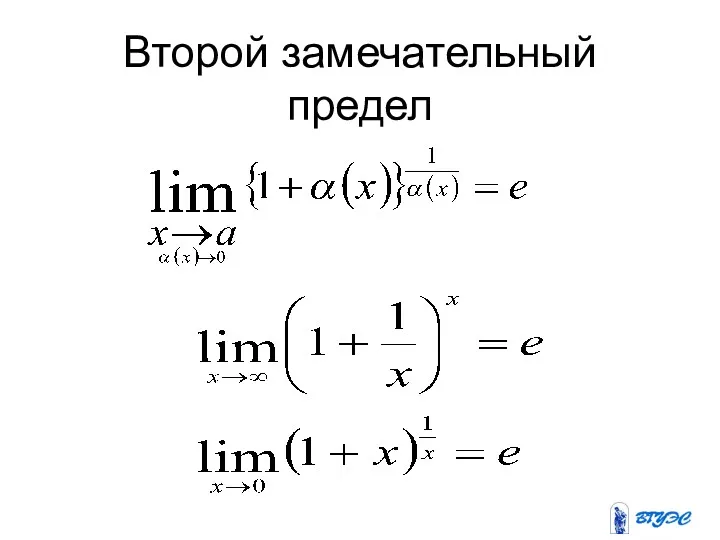
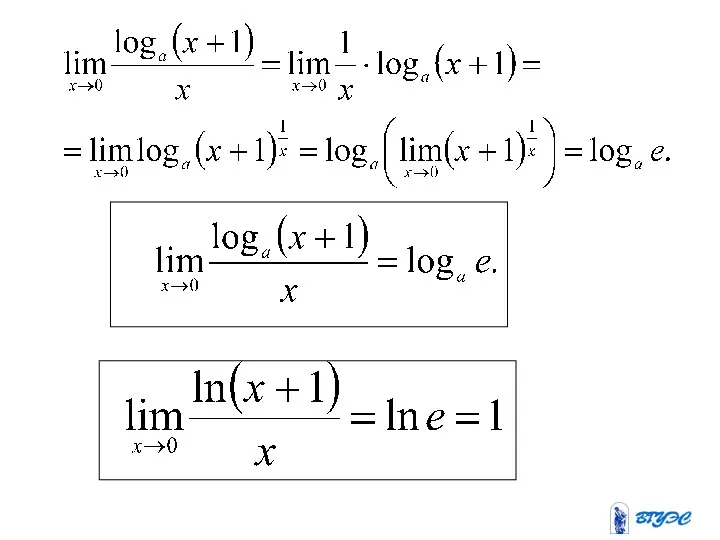








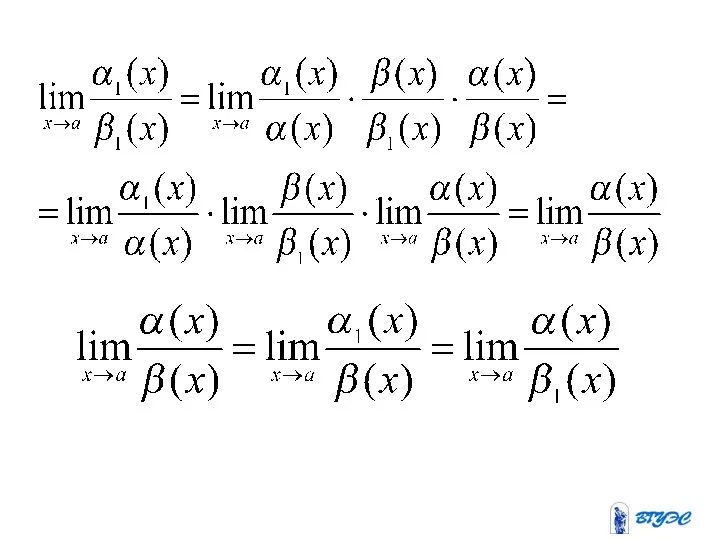

















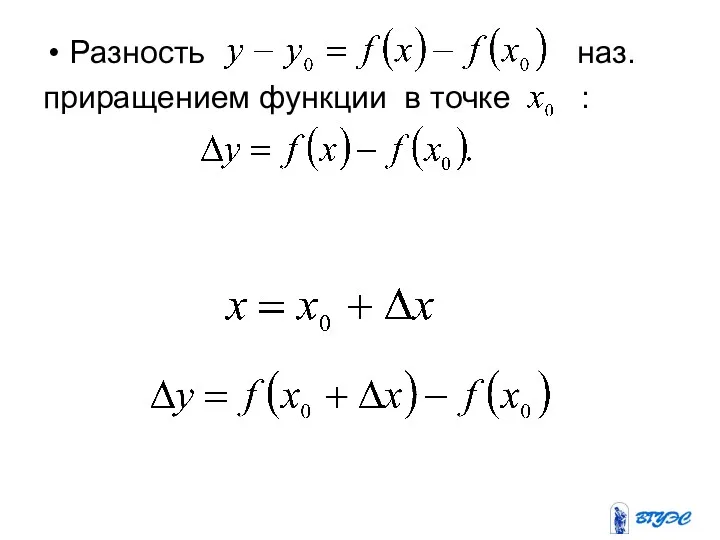
 Письменные приемы умножения многозначных чисел на однозначное число
Письменные приемы умножения многозначных чисел на однозначное число Криві другого порядку
Криві другого порядку Ознайомлення з прийомом віднімання чисел в межах 20 з переходом через десяток виду 11 - на основі десяткового складу числа
Ознайомлення з прийомом віднімання чисел в межах 20 з переходом через десяток виду 11 - на основі десяткового складу числа Открытый и опубликованный урок математики на тему: Приёмы письменного умножения вида: 4.037*4
Открытый и опубликованный урок математики на тему: Приёмы письменного умножения вида: 4.037*4 Дидактические игры по формированию элементарных математических представлений
Дидактические игры по формированию элементарных математических представлений Развитие приемов умственной деятельности. Прием сравнения
Развитие приемов умственной деятельности. Прием сравнения Решение заданий. Формулы сокращенного умножения. По материалам открытого банка задач ЕГЭ по математике
Решение заданий. Формулы сокращенного умножения. По материалам открытого банка задач ЕГЭ по математике Есептерді салыстыру
Есептерді салыстыру Сложение чисел с разными знаками
Сложение чисел с разными знаками Лекция 5. Численные методы решения нелинейных уравнений
Лекция 5. Численные методы решения нелинейных уравнений Додавання та віднімання дробів з різними знаменниками
Додавання та віднімання дробів з різними знаменниками Упростите выражение
Упростите выражение Конус. Элементы конуса
Конус. Элементы конуса Презентация по теме: Устный счет на уроке математики 2 класс
Презентация по теме: Устный счет на уроке математики 2 класс Логарифмическая функция
Логарифмическая функция Аксиома параллельных прямых (7 класс)
Аксиома параллельных прямых (7 класс) Знакомство с задачами
Знакомство с задачами Спецификация множественной регрессии
Спецификация множественной регрессии Учимся писать цифру 4
Учимся писать цифру 4 Урок математики 2 класс УМК Перспектива
Урок математики 2 класс УМК Перспектива Виды углов. (Задачи, 5 класс)
Виды углов. (Задачи, 5 класс) Законы сложения
Законы сложения Математический кубик-рубик. Натуральные числа
Математический кубик-рубик. Натуральные числа Перпендикулярные прямые
Перпендикулярные прямые Середнє арифметичне. Середнє значення величин
Середнє арифметичне. Середнє значення величин Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов Вычисление объёмов геометрических тел с помощью определённого интеграла
Вычисление объёмов геометрических тел с помощью определённого интеграла Проценты. Обобщающий урок
Проценты. Обобщающий урок