Содержание
- 2. Возникновение теории вероятностей как науки относят к средним векам, к романтическому времени королей и мушкетеров, прекрасных
- 3. Зарождение теории вероятностей началось с того, что придворный французского короля, шевалье (кавалер) де Мере (1607-1648), сам
- 4. До нас дошли два опроса де Мере к Паскалю: 1) сколько раз надо бросить две игральные
- 5. В теории вероятностей рассматриваются испытания, результаты которых нельзя предсказать заранее, а сами испытания можно повторять, хотя
- 6. Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания может произойти
- 7. Если при каждом испытании, при котором происходит событие A, происходит и событие B, то говорят, что
- 8. ПРИМЕР 1 Испытание состоит в однократном подбрасывании игральной кости с шестью гранями. Событие A – появление
- 9. ПРИМЕР 3. «Выигрыш» и «проигрыш» по одному билету денежно- вещевой лотереи – события противоположные. Событие называется
- 10. СВОЙСТВА ВЕРОЯТНОСТИ 1. Вероятность достоверного события Ω равна единице. Доказательство. Так как достоверное событие всегда происходит
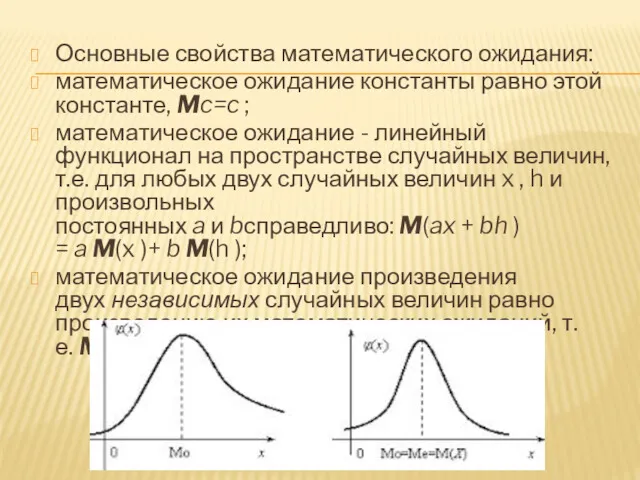
- 11. Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается
- 12. Основные свойства математического ожидания: математическое ожидание константы равно этой константе, Mc=c ; математическое ожидание - линейный
- 13. МОМЕНТЫ В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые
- 14. АСИММЕТРИЯ В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии,
- 15. ЭКСЦЕСС Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности
- 16. Средним геометрическим случайной величины, принимающей положительные значения, называется величина Название “среднее геометрическое” происходит от выражения среднего
- 17. Среднее геометрическое, вычисляется следующим образом: т.е. получилось традиционное определение среднего геометрического чисел a1, a2, …, an.
- 18. ДИСПЕРСИЯ Дисперсией конечной случайной величины x называется число по определению математического ожидания, дисперсия вычисляется по следующей
- 20. Скачать презентацию
















 Численные методы. Решение уравнений
Численные методы. Решение уравнений Математика. Вариант 6. 5 класс
Математика. Вариант 6. 5 класс Электронное сопровождение заданий учебника математики 2 класса, часть 2 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской3-я четверть
Электронное сопровождение заданий учебника математики 2 класса, часть 2 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской3-я четверть Основы научных исследований в садоводстве. Биометрия растений
Основы научных исследований в садоводстве. Биометрия растений Треугольник. Повторение
Треугольник. Повторение Способы описания САУ (Математическое описание)
Способы описания САУ (Математическое описание) Теорема Чевы
Теорема Чевы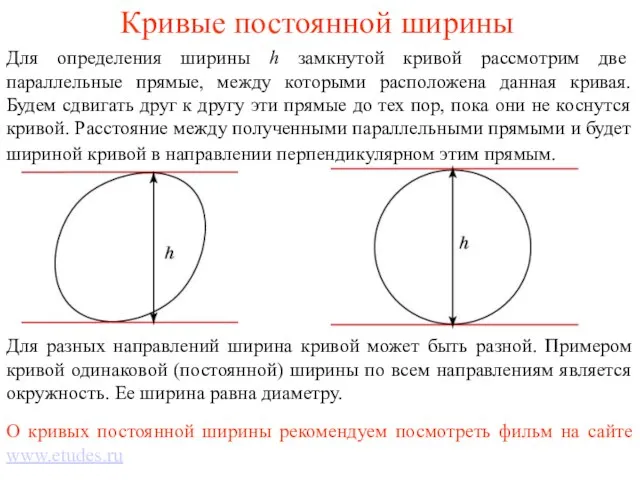 Кривые постоянной ширины
Кривые постоянной ширины Множення на 2. Тест
Множення на 2. Тест Начертательная геометрия. Пересечение прямой линии с поверхностью. (Лекция 3)
Начертательная геометрия. Пересечение прямой линии с поверхностью. (Лекция 3) Конспект урока по математике 4 класс Школа России Письменное деление
Конспект урока по математике 4 класс Школа России Письменное деление Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Лингвистика для математиков
Лингвистика для математиков Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Решение практико – ориентированных задач №1-№5 из ОГЭ
Решение практико – ориентированных задач №1-№5 из ОГЭ Мастер-класс по внеурочной деятельности. Нестандартный способ запоминания таблицы умножения.
Мастер-класс по внеурочной деятельности. Нестандартный способ запоминания таблицы умножения. Многоугольники. (5 класс)
Многоугольники. (5 класс) Графики тригонометрических функций и их свойства
Графики тригонометрических функций и их свойства Площади простых фигур. Игра Поле чудес, для 8 класса
Площади простых фигур. Игра Поле чудес, для 8 класса Подготовка к ЕГЭ. Задачи по геометрии в вариантах ЕГЭ
Подготовка к ЕГЭ. Задачи по геометрии в вариантах ЕГЭ Початкові та центральні моменти в теорії ймовірностей і математичній статистиці
Початкові та центральні моменти в теорії ймовірностей і математичній статистиці Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике)
Решение задач по теории вероятности (по материалам открытого банка задач ЕГЭ по математике) Функции, их свойства и графики. Урок – повторение в 9 классе
Функции, их свойства и графики. Урок – повторение в 9 классе Пирамида
Пирамида Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Использование презентаций PowerPoint на уроках математики при построении графиков функции
Использование презентаций PowerPoint на уроках математики при построении графиков функции Решение задач с помощью уравнений
Решение задач с помощью уравнений Свойства четырехугольников. Решение задач
Свойства четырехугольников. Решение задач