Матриці та визначники. Матриці та їх властивості. Лінійні операції над матрицями. Визначники та їх властивості презентация
Содержание
- 2. §1 МАТРИЦІ ТА ВИЗНАЧНИКИ 1.1 Матриці та їх властивості Матрицею розміру m×n називається сукупність чисел, розташованих
- 3. називається вектор-стовпець, а матриця A=[a1 a2…an] розміру 1×n, що складається з одного рядка – вектор-рядок. Матриця
- 4. Квадратна матриця, в якої всі елементи aij дорівнюють 0 називається нульовою матрицею. називається одиничною. Матриця 1.2
- 5. Матриця -А (мінус А)називається матрицею протилежною А. 2. Додавання Для того, чтоб додать дві матриці A
- 6. 3. Множення на число Для того, чтоб помножити матрицю А на число α∈R необхідно кажен элемент
- 7. 4. Множення на вектор-стовпчик Для множення m×n матриці А на вектор-стовпчик х необхідно, щоб число стовпців
- 8. Приклад:
- 9. Нехай і m×n і n×k матриці (узгоджені матриці) відповідно – число стовців матриці а дорівнює числу
- 10. Приклад: Зайти добуток матриць і Матриця АТ , отримана з даной матриці А шляхом заміни рядків
- 11. 1.3 Визначники та їх властивості Поняття визначника вводиться тільки для квадратних матриць. Визначником n-го порядку матриці
- 12. Правило трикутника:три додатних члена визначника третього порядку є добутком елементів головної діагоналі і елементів, що знаходяться
- 13. Властивості визначників n-го порядку: 1. Визначник матриці А дорівнює визначнику транспонованою матриці, 2. Якщо всі елементи
- 14. 7. Значення визначника не зміниться, якщо до елементів його рядка додати відповідні елементи іншого рядка, помножені
- 15. ⎜A⎜ =ai1Ai1+ai2Ai2+…+ainAin, i=1..n. 8. Визначник дорівнює сумі добутків елементів будь-якого його рядка на відповідні алгебраїчні доповнення
- 17. Скачать презентацию

![називається вектор-стовпець, а матриця A=[a1 a2…an] розміру 1×n, що складається](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/248460/slide-2.jpg)




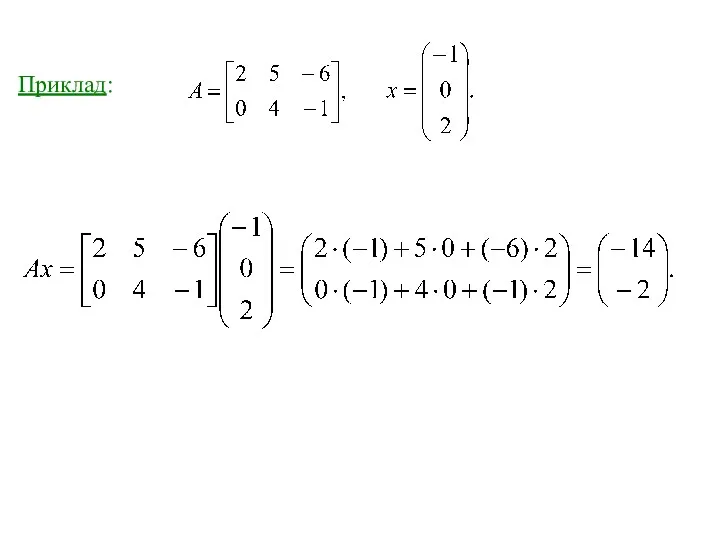







 Десятичные дроби
Десятичные дроби Смежные и вертикальные углы. Виды углов
Смежные и вертикальные углы. Виды углов Решение заданий ЕГЭ по математике профильного уровня (задание № 14)
Решение заданий ЕГЭ по математике профильного уровня (задание № 14) Математична степінь з раціональним показником, та її властивості
Математична степінь з раціональним показником, та її властивості Действия с целыми числами. 6 класс
Действия с целыми числами. 6 класс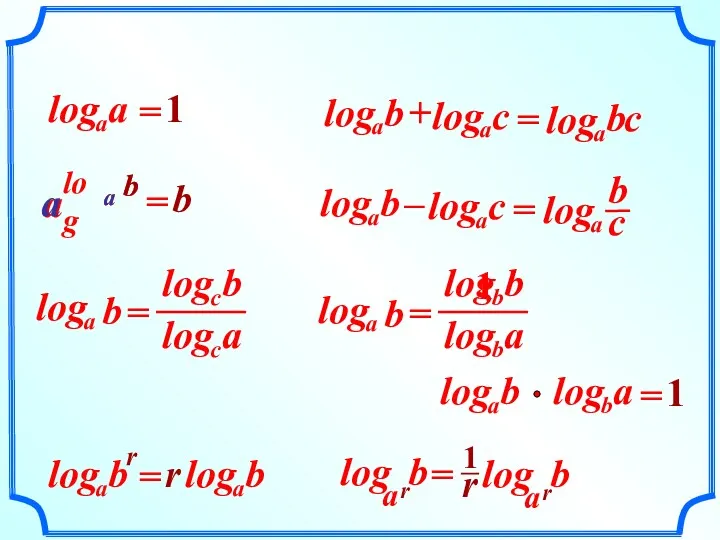 Свойства логарифмов
Свойства логарифмов Конспект урока математики в 3 классе Прямая. Непересекающиеся прямые
Конспект урока математики в 3 классе Прямая. Непересекающиеся прямые Разработка открытого урока математики
Разработка открытого урока математики Урок математики в 1 классе по теме: Вычитание(ПрограммаНачальная школа ХХI века)
Урок математики в 1 классе по теме: Вычитание(ПрограммаНачальная школа ХХI века) Линейная функция и её график
Линейная функция и её график Вписанная в треугольник окружность
Вписанная в треугольник окружность Отображения и функции
Отображения и функции Состав числа 12
Состав числа 12 Экология на уроках математики
Экология на уроках математики Признаки делимости. Мультимедийный комбинированный урок. 5 класс
Признаки делимости. Мультимедийный комбинированный урок. 5 класс Свойства логарифмов
Свойства логарифмов Гамильтоновы графы
Гамильтоновы графы Презентация по теме Числа от1 до 100. Сложение и вычитание.
Презентация по теме Числа от1 до 100. Сложение и вычитание. Криволинейные интегралы
Криволинейные интегралы Параллельные прямые. (7 класс)
Параллельные прямые. (7 класс) Презентация к уроку математики Что узнали. Чему научились. 2 класс
Презентация к уроку математики Что узнали. Чему научились. 2 класс Условия Гаусса-Маркова
Условия Гаусса-Маркова Приёмы умножения и деления на 10. Устный счёт
Приёмы умножения и деления на 10. Устный счёт Метод алгебраического сложения
Метод алгебраического сложения Устный счет для 2 класса по УМК Начальная школа 21 века
Устный счет для 2 класса по УМК Начальная школа 21 века Периметр прямоугольника
Периметр прямоугольника Самый умный математик
Самый умный математик Появление дробей. 5 класс
Появление дробей. 5 класс