Содержание
- 2. Матрица. Прямоугольная таблица чисел называется матрицей. Если в указанной таблице m строк и n столбцов, то
- 3. или Числа называются элементами матрицы А.
- 4. Главная диагональ Для квадратной матрицы совокупность чисел называется ее главной диагональю.
- 5. Равные матрицы. Две матрицы считаются равными, если они имеют одинаковые размеры и их соответственные элементы равны
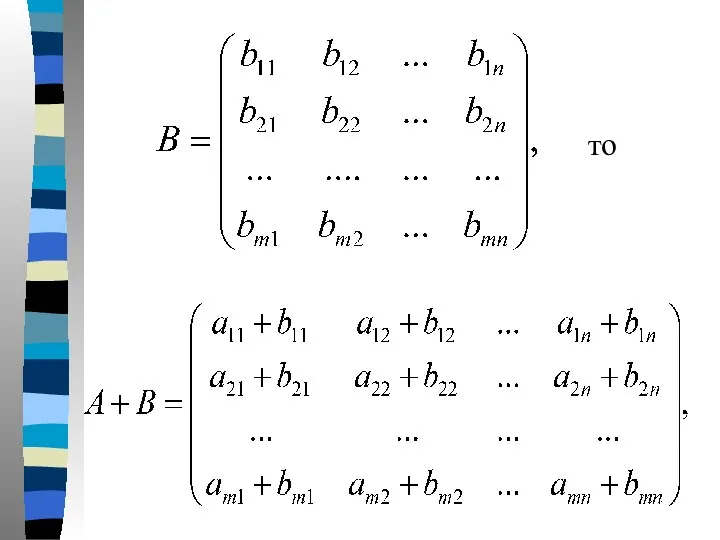
- 6. Сложение матриц. Если две матрицы имеют одинаковые размеры, то их можно сложить, складывая соответственные элементы. Так,
- 7. то
- 8. или
- 9. Умножение матрицы на число Всякую матрицу можно умножить на любое число согласно следующему определению:
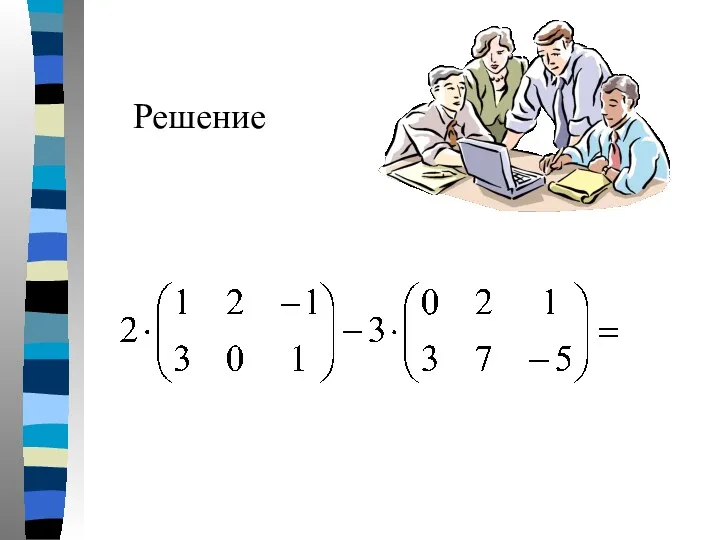
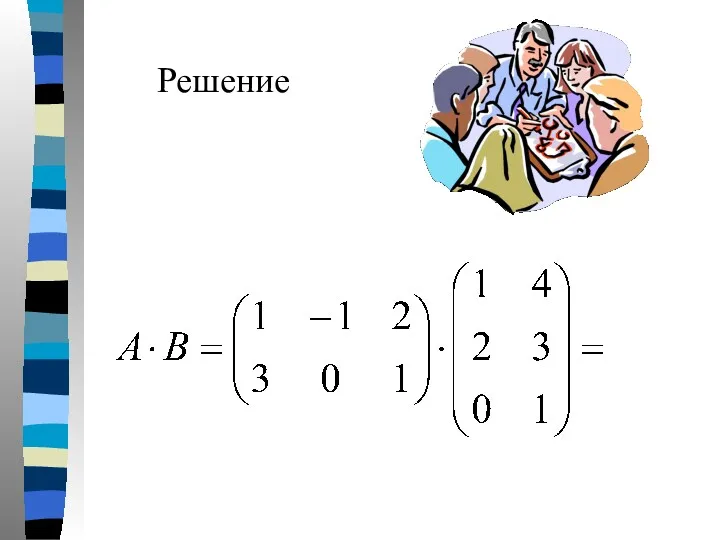
- 10. Пример 1. Даны матрицы А и В Найти матрицу
- 11. Решение
- 13. Свойства. Легко видеть, что операции сложения и умножения матрицы на число удовлетворяют следующим свойствам: 1.свойство коммуникативности
- 14. 2. Свойство ассоциативности 3.
- 15. 4. 5.
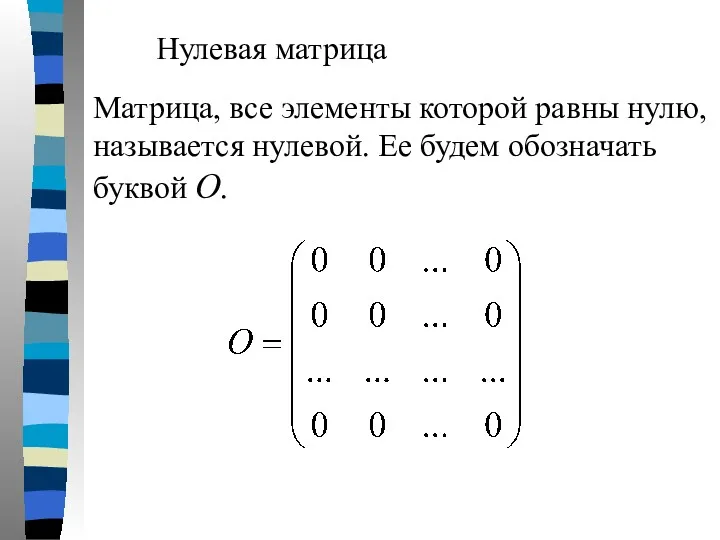
- 16. Нулевая матрица Матрица, все элементы которой равны нулю, называется нулевой. Ее будем обозначать буквой О.
- 17. Умножение матриц Пусть у нас имеются две матрицы
- 18. Здесь число столбцов первой матрицы равно числу строк второй. Тогда произведение матрицы А на матрицу В
- 19. где
- 20. Оператор суммирования Если воспользоваться оператором суммирования , то
- 21. Произведение матриц Произведение матриц А и В записывается так:
- 22. Пример 1 Умножить матрицу на матрицу
- 23. Решение
- 25. Транспонирование матриц Пусть у нас имеется матрица . Если каждую строку этой матрицы заменить ее столбцом
- 27. Определители второго и третьего порядков По определенному правилу каждой квадратной матрице А ставится определенное число, которое
- 28. Если порядок матрицы А равен единице, то Для квадратной матрицы второго порядка
- 29. Опираясь на это определение определителя второго порядка дадим определение определителя третьего порядка. Если , то
- 32. Для запоминания правила вычисления определителя третьего порядка используется правило треугольников или правило Саррюса. Оно состоит в
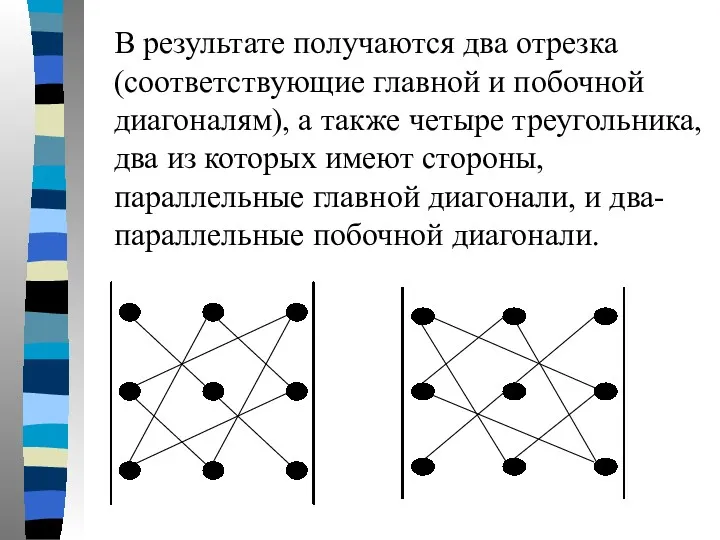
- 33. В результате получаются два отрезка (соответствующие главной и побочной диагоналям), а также четыре треугольника, два из
- 34. Главной диагонали и тем двум треугольникам, основания которых параллельны главной диагонали, соответствуют произведения со знаком «+»,
- 35. Решение:
- 36. Обратная матрица Пусть у нас имеется квадратная матрица Матрица называется обратной к матрице А, если
- 37. где называется символом Кронекера.
- 38. Квадратная матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.
- 39. Решение. Сначала проверим, является ли определитель матрицы А отличным от нуля:
- 40. Отсюда вытекает, что матрица А невырожденная и у нее есть обратная:
- 41. В нашем случае:
- 44. Отсюда
- 45. Ранг матрицы Пусть у нас имеется матрица содержащая m строк и n столбцов:
- 46. Выделим в этой матрице k строк k столбцов элементов, стоящих на пересечении выделенных строк и столбцов,
- 47. Пример. Найти ранг матрицы У этой матрицы 12 миноров первого порядка, 18 миноров второго порядка:
- 50. и наконец 4 минора третьего порядка:
- 51. Нетрудно проверить, что все миноры третьего порядка матрицы А равны нулю, а миноры второго порядка во
- 52. При вычислении ранга матрицы существенную роль играют элементарные преобразования матрицы: 1) умножение элементов любой строки (столбца)
- 53. При элементарных преобразованиях ранг матрицы не изменяется. С помощью элементарных преобразований любую матрицу можно привести к
- 54. где на «главной диагонали» стоит r единиц, а все остальные элементы матрицы равны нулю. Ранг такой
- 55. Системы линейных уравнений Основные понятия и определения Системой линейных алгебраических уравнений с n переменными х1, х2,
- 56. Здесь числа называются коэффициентами системы, а числа b1, b2, …,bm-ее свободными членами. Если b1= b2=…=bm=0, то
- 57. Решением системы называется всякая упорядоченная совокупность n чисел (с1, с2, …, сn), которая при подстановке в
- 58. Совместные системы делятся на определенные и неопределенные. Система, которая имеет только одно решение, называется определенной. Если
- 59. Систему удобно записать в матричной форме, для чего введем необходимые понятия. Матрица элементы которой являются коэффициентами
- 60. Введем еще две матрицы, каждая из которых состоит из одного столбца (матрицы-столбца): Это матрица-столбец переменных и
- 61. У матрицы А n столбцов, а у матрицы X n строк, поэтому А можно умножить на
- 62. Как показывают равенства, каждый элемент матрицы столбца АХ есть соответствующий элемент матрицы В. Отсюда в соответствии
- 63. Введем в рассмотрение матрицы-столбцы тогда система уравнений может быть записана так:
- 64. Две системы линейных алгебраических уравнений называются эквивалентными (равносильными), если всякое решение одной из них является решением
- 65. 1) умножение на число, отличное от нуля одного из уравнений системы; 2) прибавление к одному уравнению
- 66. Формула Крамера Пусть дана система n линейных алгебраических уравнений с n-переменными (неизвестными):
- 67. Если определитель матрицы системы отличен от нуля и система совместна, то она и определенная. Если система
- 68. Пример. Решить систему линейных уравнений
- 69. Решение. Вычислим определитель системы следующим образом. Из первой строки вычтем удвоенную третью строку, из третьей-четвертую, тогда
- 72. Определитель следовательно, правило Крамера применимо к системе. Составим и вычислим определители
- 74. Отсюда искомое решение данной системы
- 76. Скачать презентацию





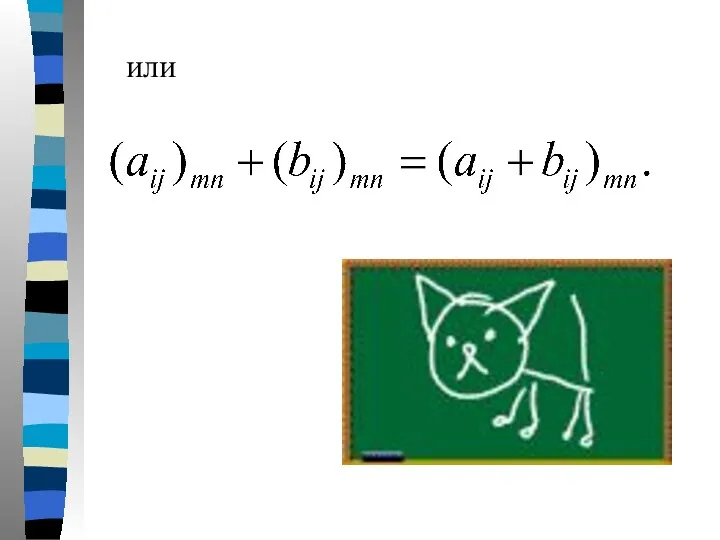


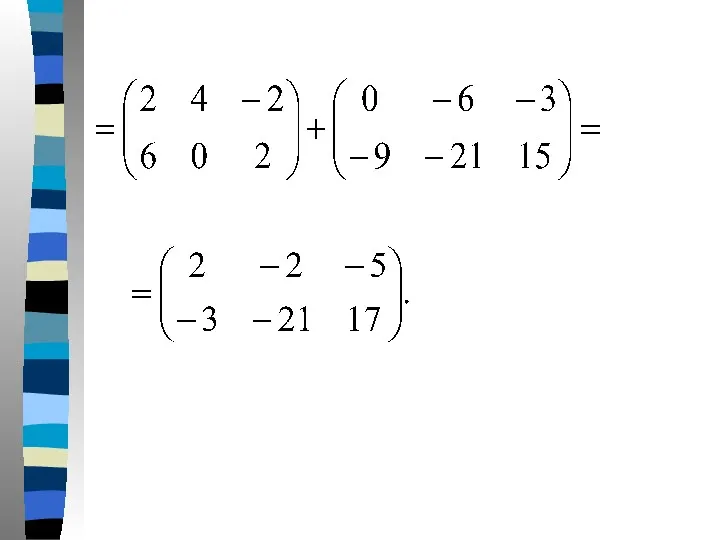

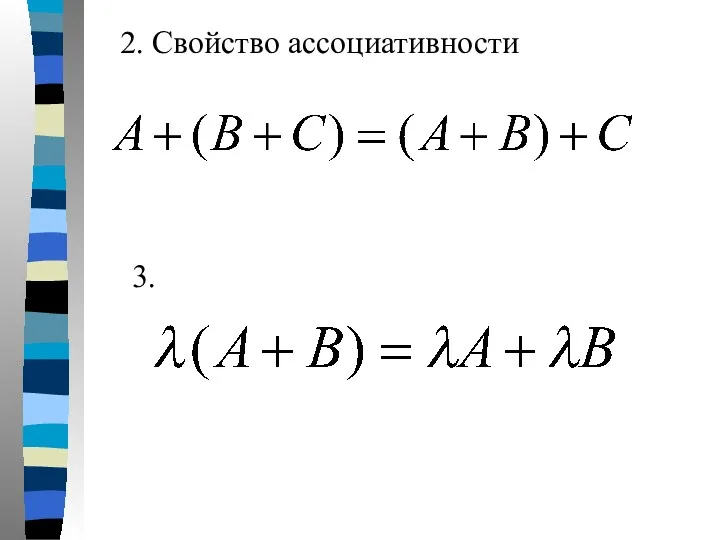
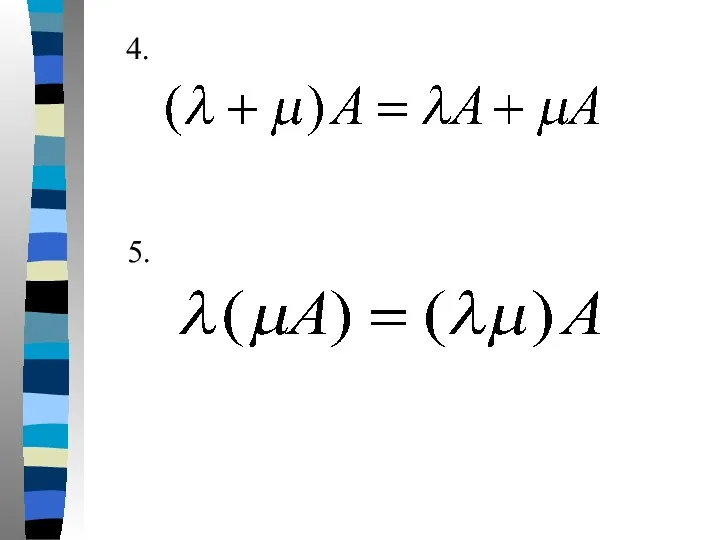


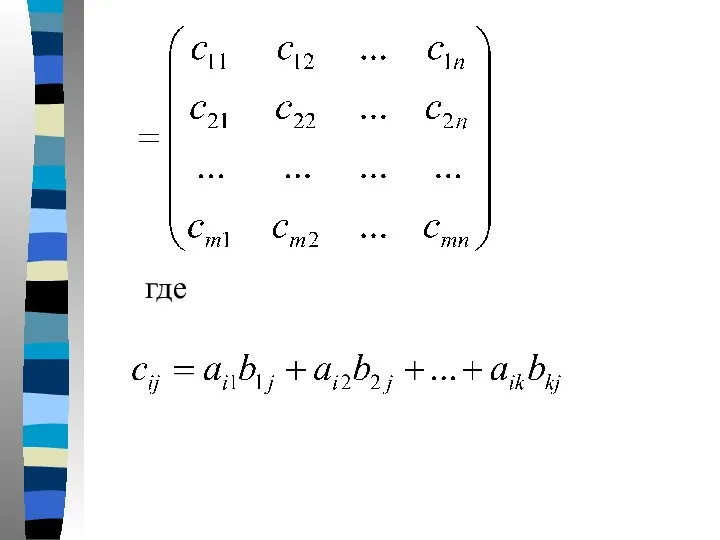



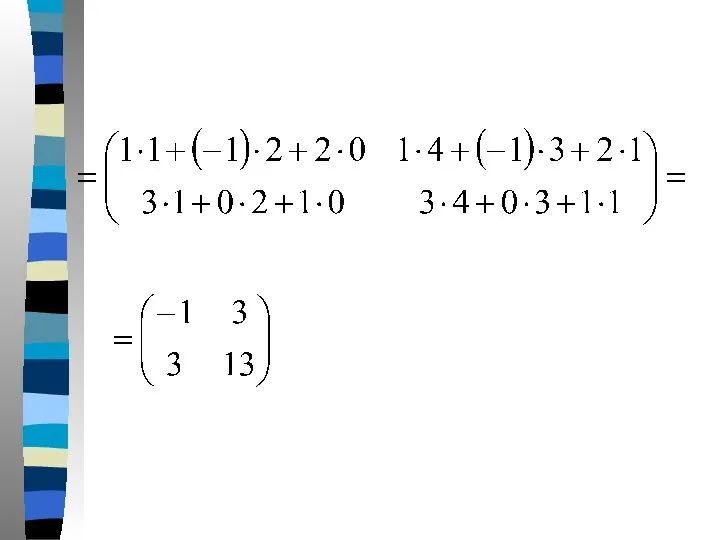





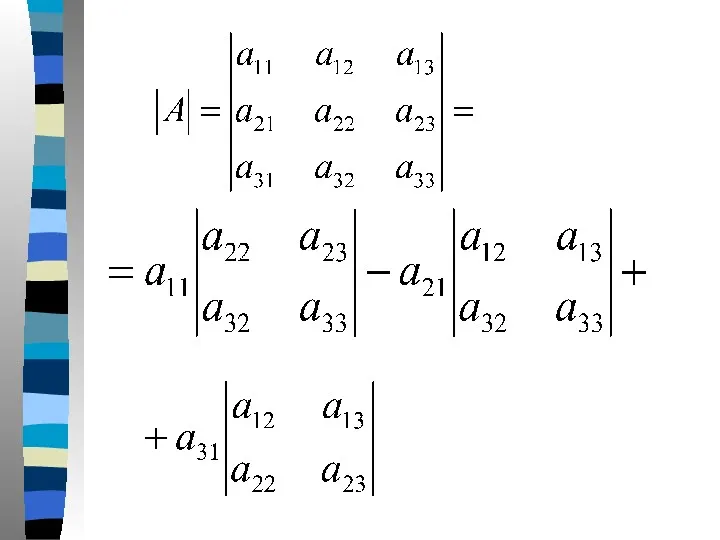
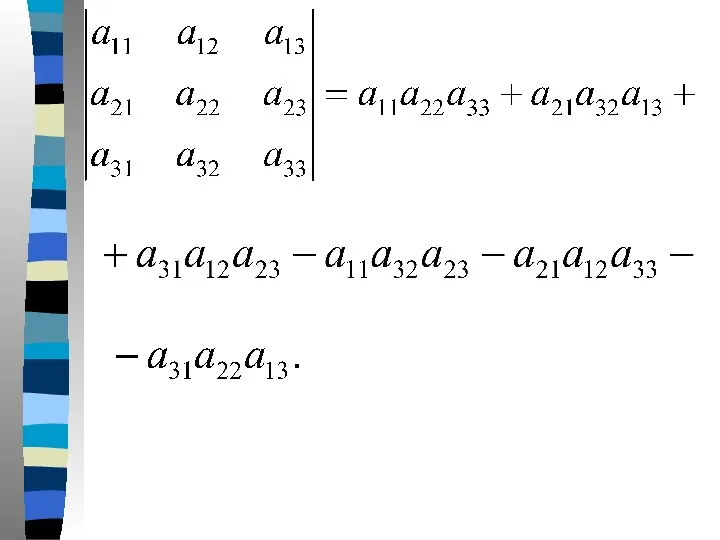








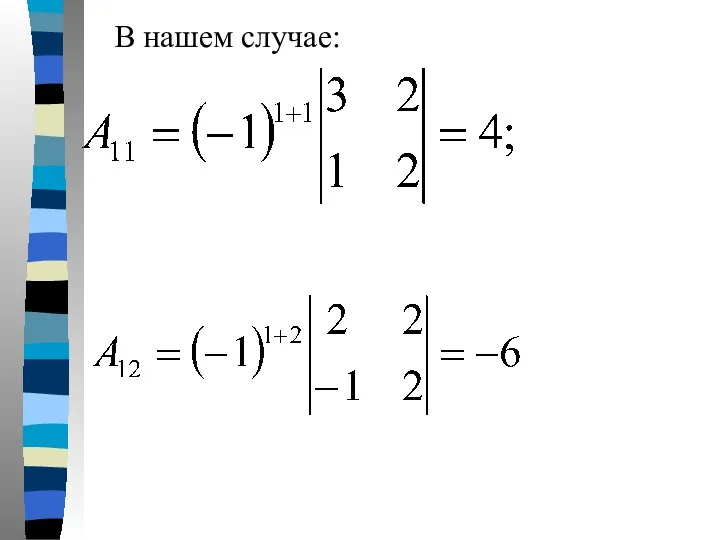
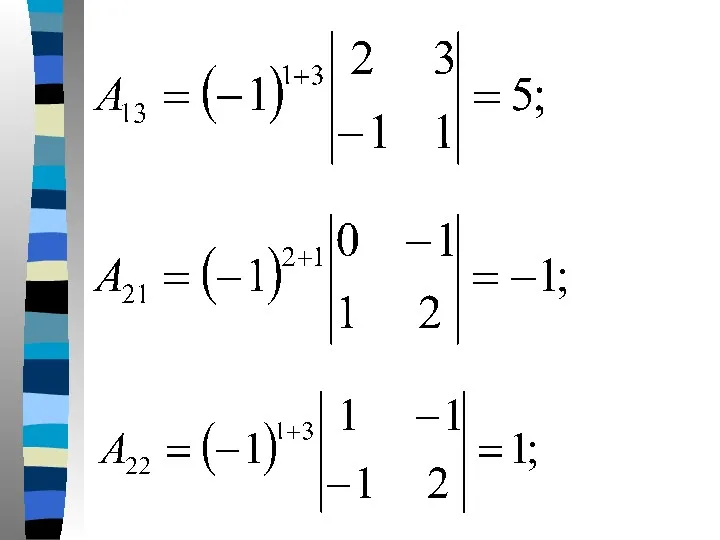
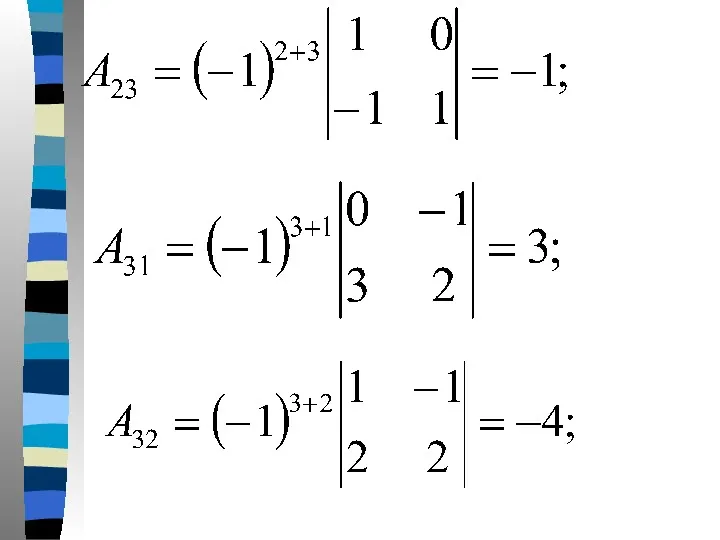
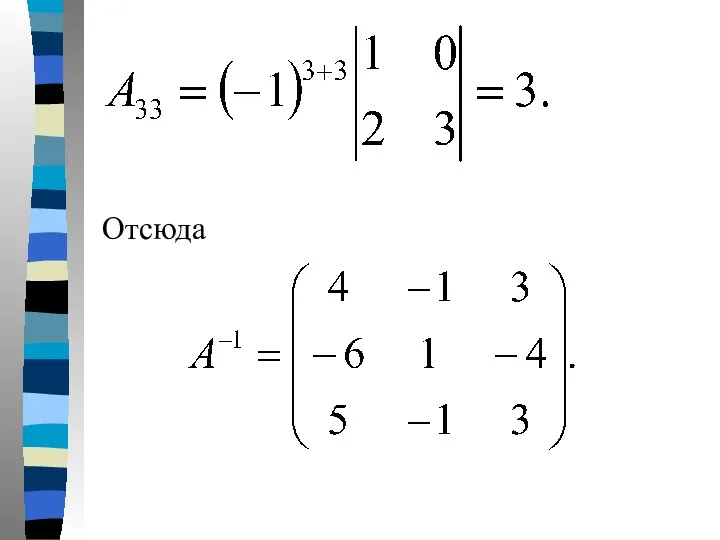




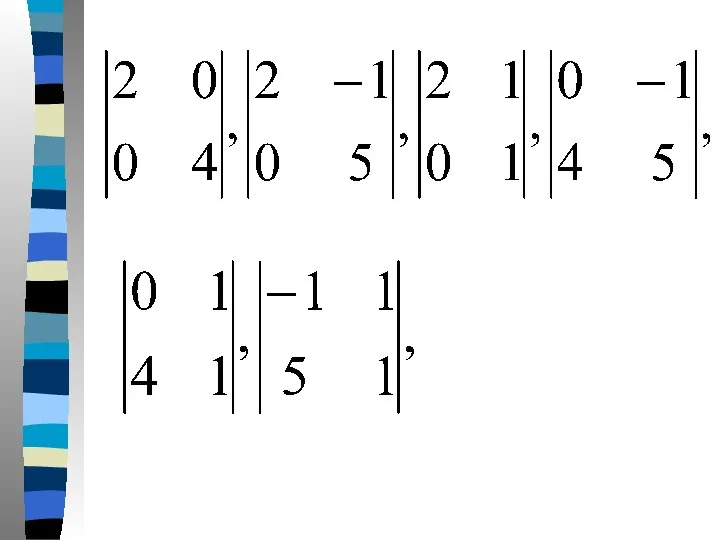




















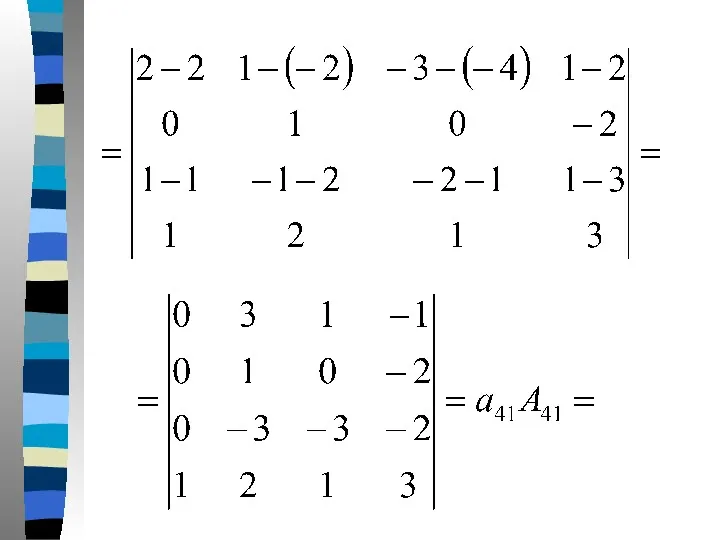
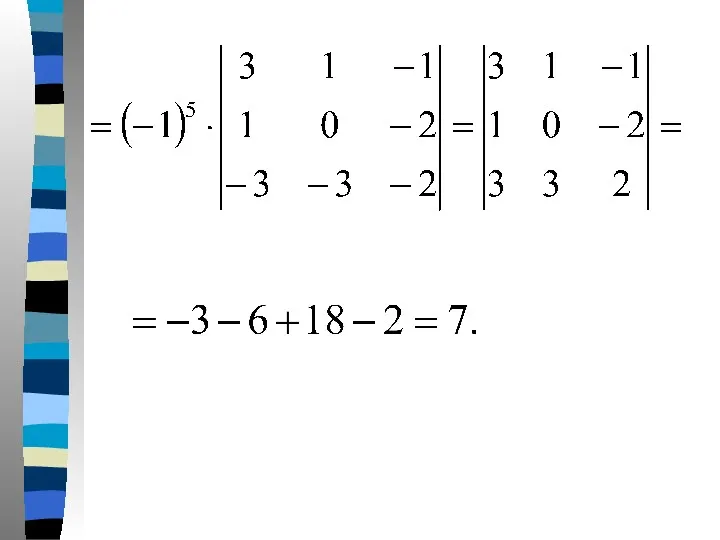

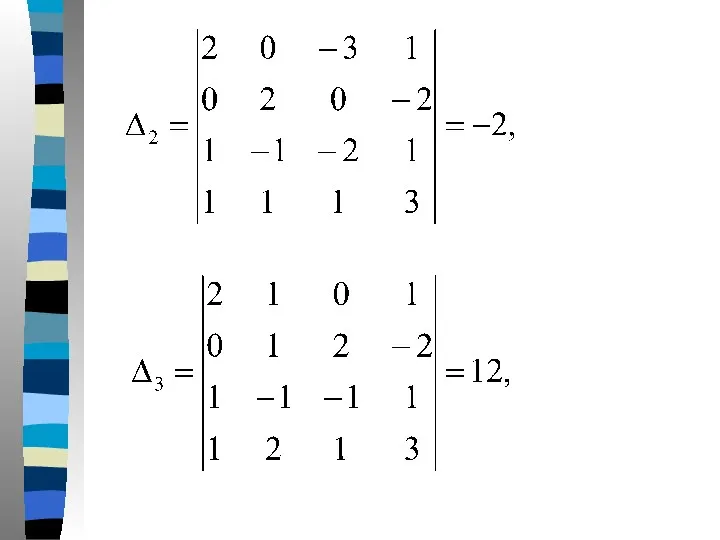

 Параллелограмм и трапеция. Задания для устного счета. Упражнение 3. 8 класс
Параллелограмм и трапеция. Задания для устного счета. Упражнение 3. 8 класс Птицы из красной книги Башкортостана. Региональный компонент на уроках математики в начальной школе
Птицы из красной книги Башкортостана. Региональный компонент на уроках математики в начальной школе Единицы длины. 5 класс
Единицы длины. 5 класс Поиграем! Вперёд за волшебным клубочком. 1класс
Поиграем! Вперёд за волшебным клубочком. 1класс Определенный интеграл. Задачи, приводящие к понятию определенного интеграла
Определенный интеграл. Задачи, приводящие к понятию определенного интеграла Презентация к занятию Путешествие в страну Заниматика
Презентация к занятию Путешествие в страну Заниматика Похідна. Правила диференціювання
Похідна. Правила диференціювання Презентация к уроку Конкретный смысл действия деления.
Презентация к уроку Конкретный смысл действия деления. Взаимное положение прямой и плоскости, двух плоскостей
Взаимное положение прямой и плоскости, двух плоскостей Решение задач на составление уравнений
Решение задач на составление уравнений Использование информационных технологий в экономических моделях
Использование информационных технологий в экономических моделях Тема урока: числа от 1 до 8
Тема урока: числа от 1 до 8 Деление десятичных дробей
Деление десятичных дробей Презентация по теме Решение неравенства 4 класс по программе Л. Г. Петерсон
Презентация по теме Решение неравенства 4 класс по программе Л. Г. Петерсон Презентация по математике Формула стоимости 3 класс
Презентация по математике Формула стоимости 3 класс Устный счет. Сложение с переходом через десяток. Часть 2
Устный счет. Сложение с переходом через десяток. Часть 2 Обобщающее повторение курса математики — залог успешности сдачи Единого государственного экзамена
Обобщающее повторение курса математики — залог успешности сдачи Единого государственного экзамена Тригонометриялық өрнектерді түрлендіру
Тригонометриялық өрнектерді түрлендіру Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве
Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве Преобразование выражений при решений уравнений. Задание для устного счета. Упражнение 25. 6 класс
Преобразование выражений при решений уравнений. Задание для устного счета. Упражнение 25. 6 класс Презентация Схемы задач
Презентация Схемы задач Прямая и обратная пропорциональные зависимости. 6 класс
Прямая и обратная пропорциональные зависимости. 6 класс Понятие цилиндра. Площадь поверхности цилиндра
Понятие цилиндра. Площадь поверхности цилиндра Многочлены
Многочлены Двугранный угол
Двугранный угол Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20
Презентация к уроку математики во 2 классе по теме Приёмы вычислений для случаев вида 36 + 2, 36 + 20 Основные свойства простейших геометрических фигур, 7 класс
Основные свойства простейших геометрических фигур, 7 класс Что в остатке
Что в остатке