Содержание
- 2. Введение в метод Симплекс-метод, известный также под названием метода последовательного улучшения плана, впервые разработал Г. Данциг
- 3. Симплексные методы оптимизации Симплекс – это фигура, имеющая на 1 вершину больше, чем размерность факторного пространства:
- 4. X10
- 5. Симплексные методы оптимизации, алгоритм 1. Оцениваются априорные сведения о процессе и выбираются интервалы варьирования по каждому
- 6. 3. Проводится первоначальная ориентация симплекса в факторном пространстве: вдоль одной из осей факторного пространства (а, б),
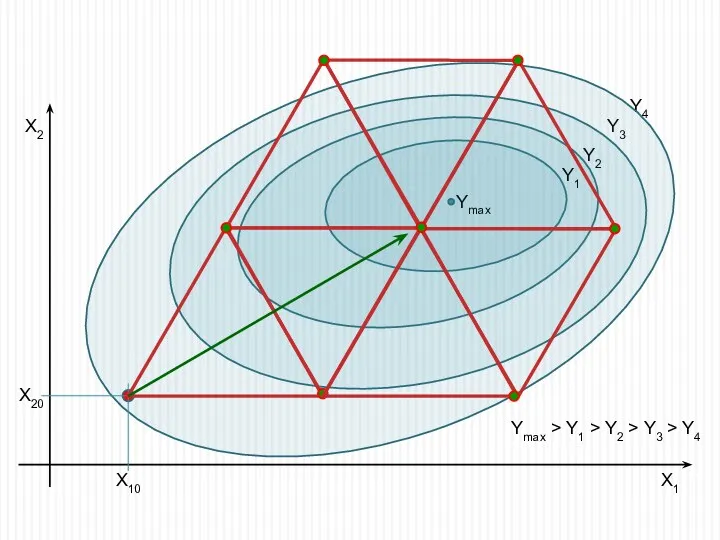
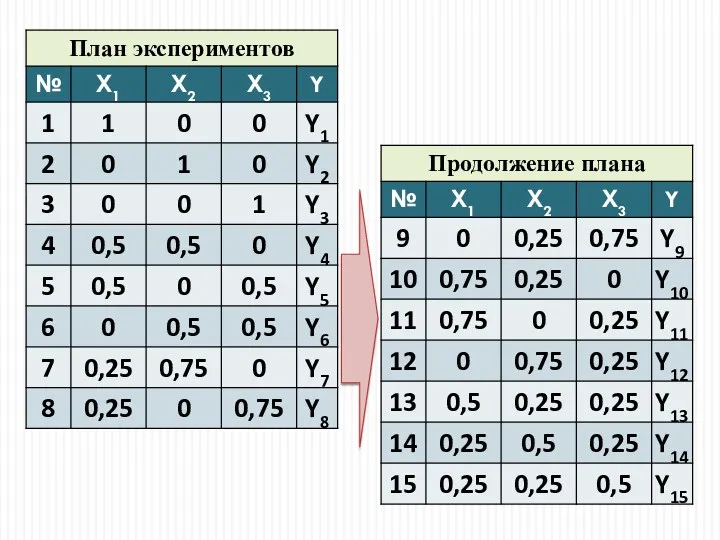
- 7. Симплексные методы оптимизации, расчеты Построение первого симплекса выполняется по геометрическим формулам для построения равносторонней фигуры, например,
- 8. Как только симплекс завершит оборот вокруг экстремума, можно переходить к расчету коэффициентов уравнения регрессии в виде
- 9. Факторный эксперимент при изучении смесевых систем Задача факторного эксперимента при изучении смесевых систем не отличается от
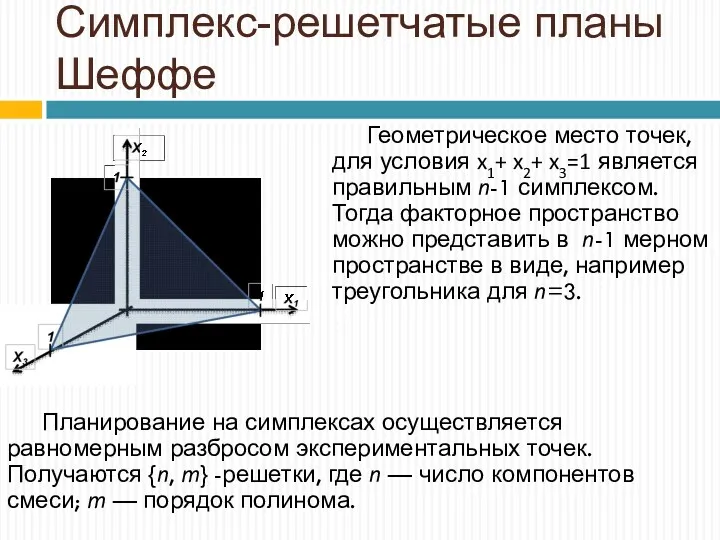
- 10. Симплекс-решетчатые планы Шеффе Геометрическое место точек, для условия x1+ x2+ x3=1 является правильным n-1 симплексом. Тогда
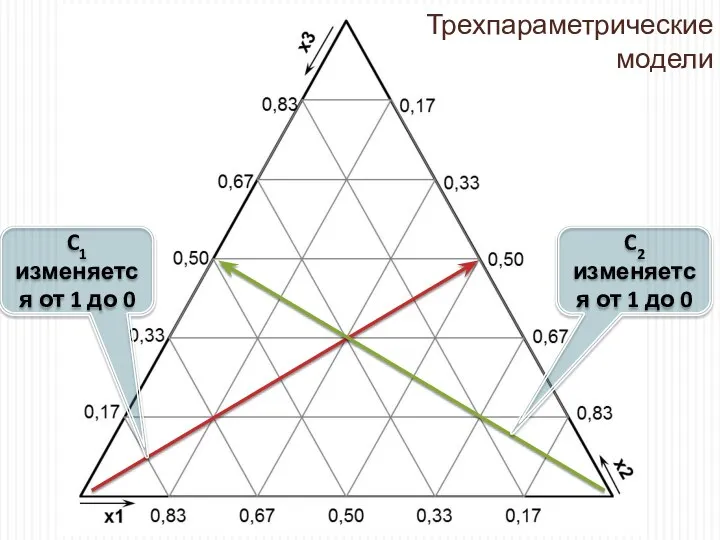
- 11. C1 изменяется от 1 до 0 C2 изменяется от 1 до 0 Трехпараметрические модели
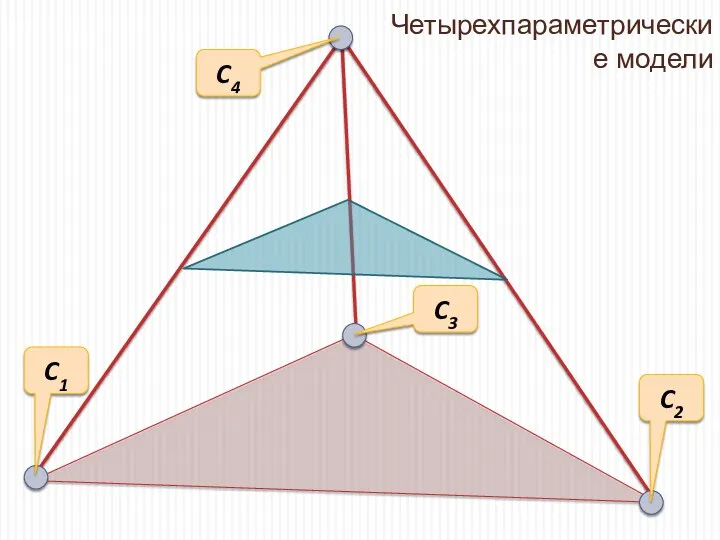
- 12. Четырехпараметрические модели C1 C3 C2 C4
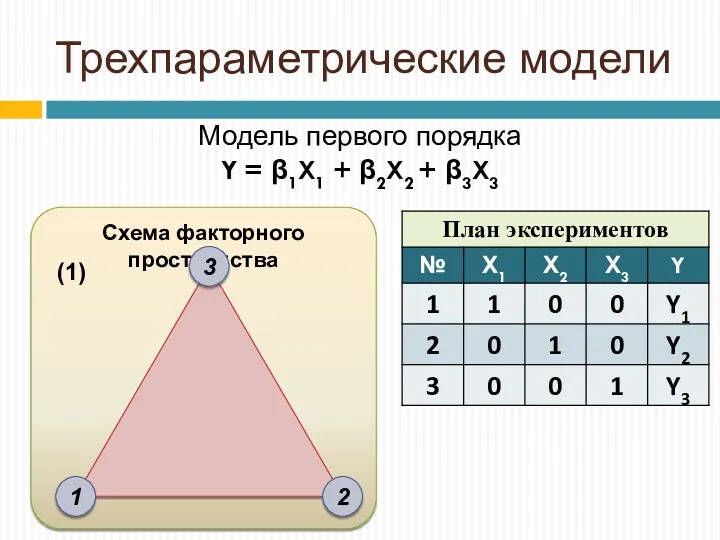
- 13. Схема факторного пространства Трехпараметрические модели Модель первого порядка Y = β1X1 + β2X2 + β3X3 1
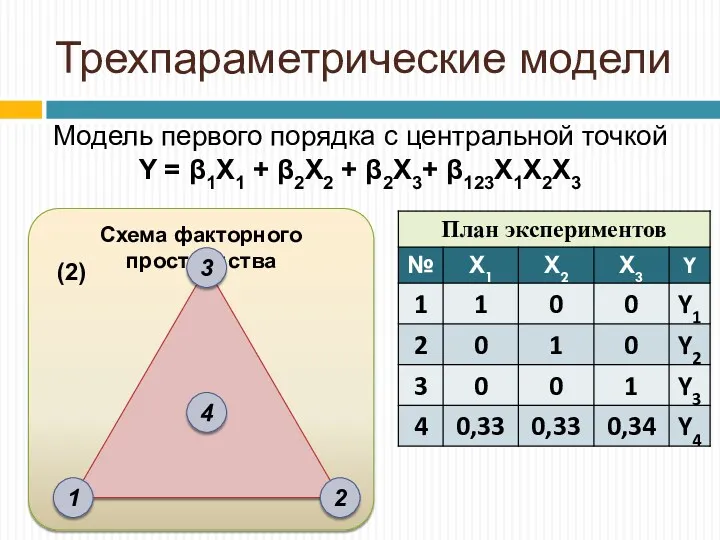
- 14. Схема факторного пространства Трехпараметрические модели Модель первого порядка с центральной точкой Y = β1X1 + β2X2
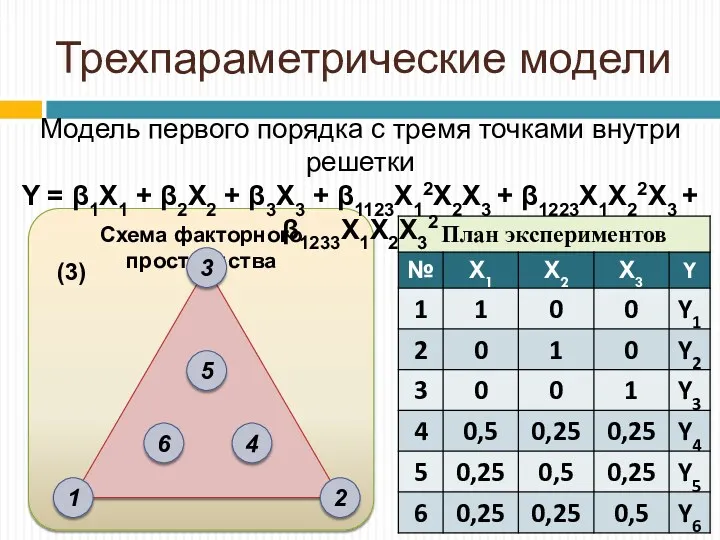
- 15. Схема факторного пространства Трехпараметрические модели Модель первого порядка с тремя точками внутри решетки Y = β1X1
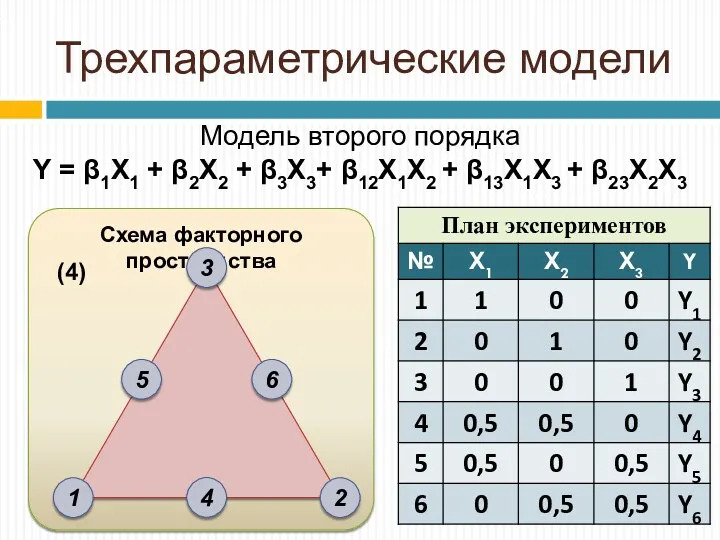
- 16. Схема факторного пространства Трехпараметрические модели Модель второго порядка Y = β1X1 + β2X2 + β3X3+ β12Х1Х2
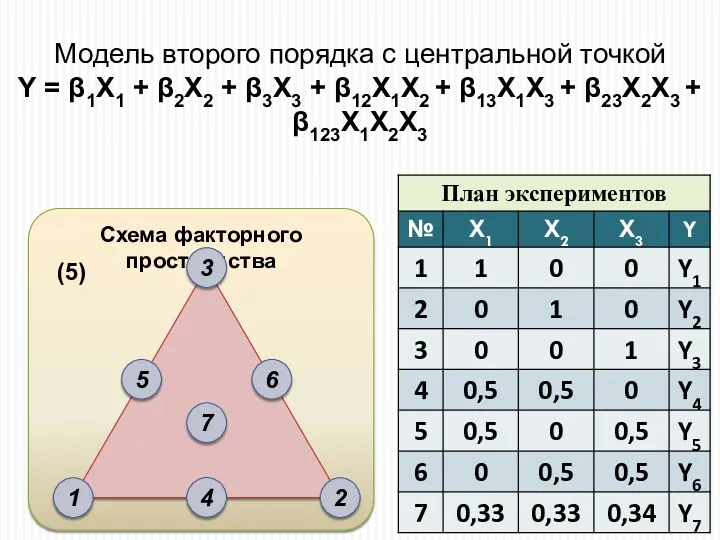
- 17. Схема факторного пространства Модель второго порядка с центральной точкой Y = β1X1 + β2X2 + β3X3
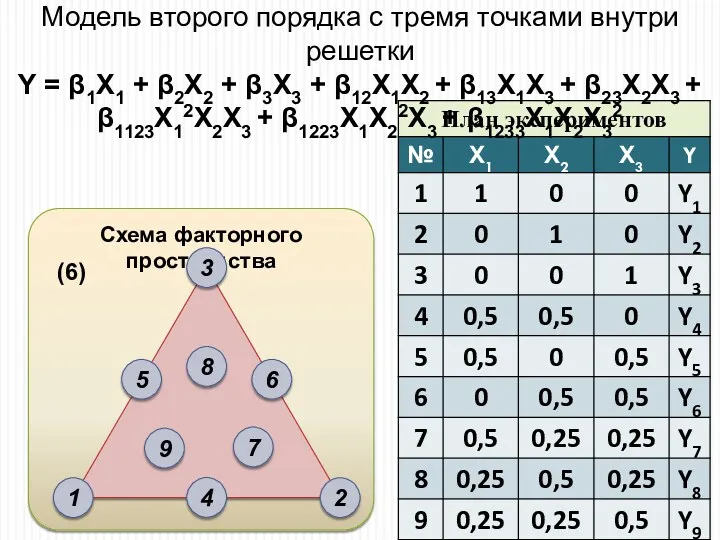
- 18. Схема факторного пространства Модель второго порядка с тремя точками внутри решетки Y = β1X1 + β2X2
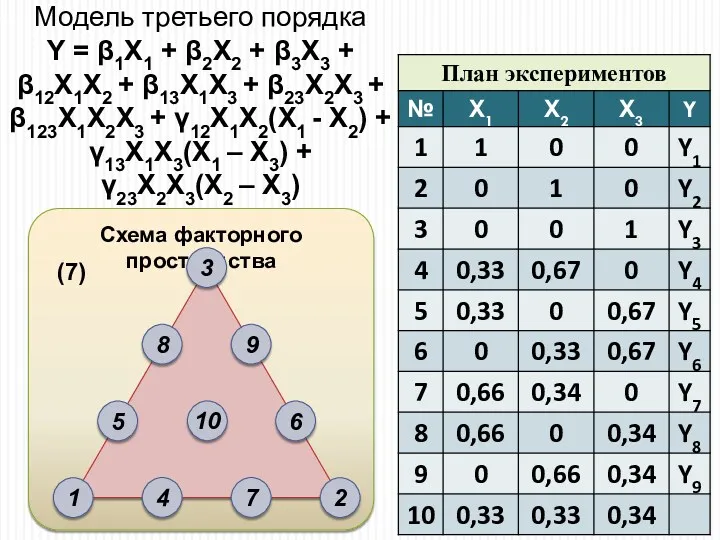
- 19. Схема факторного пространства Модель третьего порядка Y = β1X1 + β2X2 + β3X3 + β12Х1Х2 +
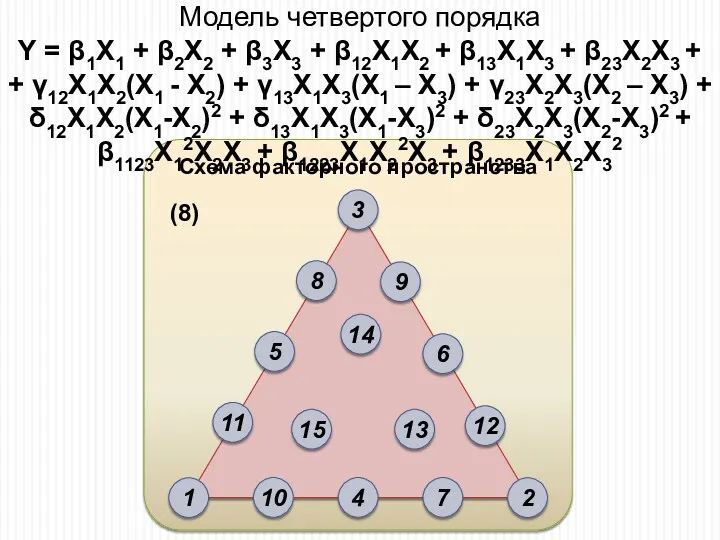
- 20. Схема факторного пространства Модель четвертого порядка Y = β1X1 + β2X2 + β3X3 + β12Х1Х2 +
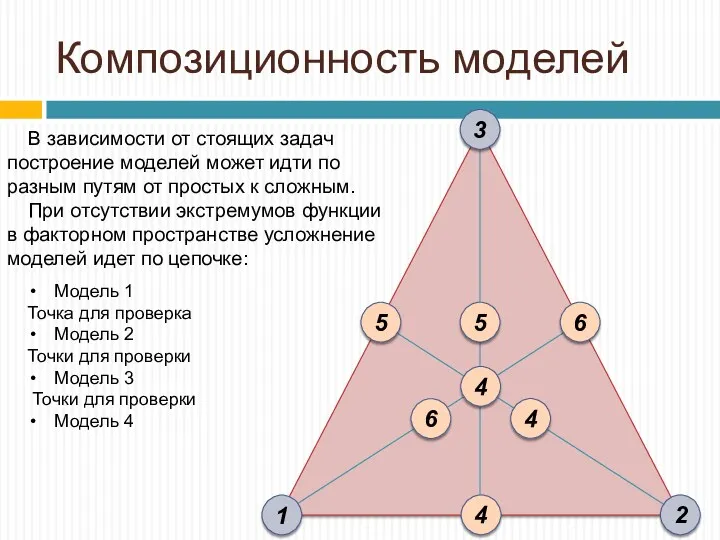
- 22. Композиционность моделей В зависимости от стоящих задач построение моделей может идти по разным путям от простых
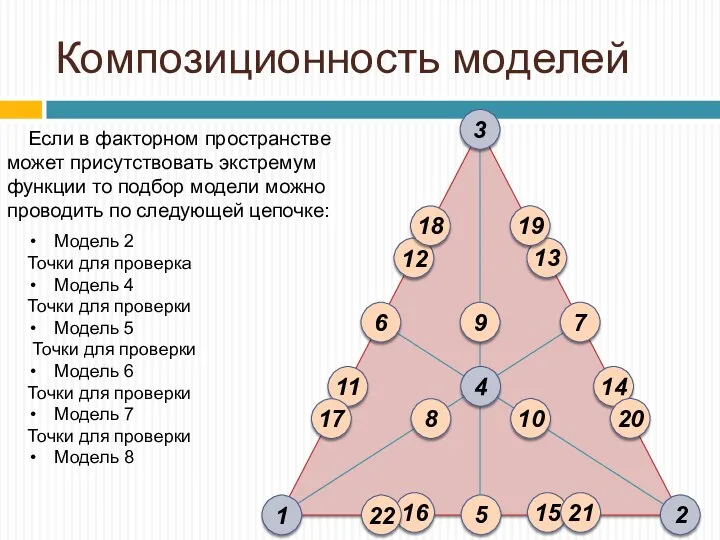
- 23. Композиционность моделей Если в факторном пространстве может присутствовать экстремум функции то подбор модели можно проводить по
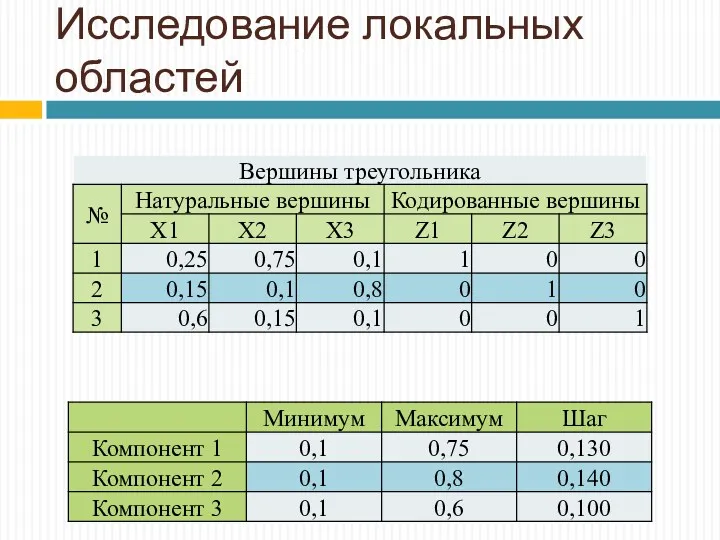
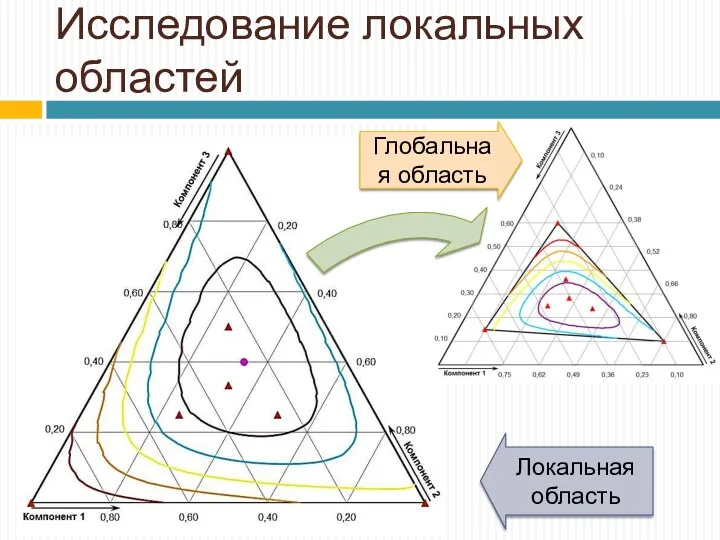
- 24. Исследование локальных областей
- 25. Исследование локальных областей Глобальная область Локальная область
- 26. Расчеты коэффициентов Обычно все эти схемы являются насыщенными, имеют равное число опытов и неизвестных коэффициентов в
- 27. Расчет средствами MS Excel С другой стороны можно пользоваться стандартными решениями (метод наименьших квадратов и «Поиск
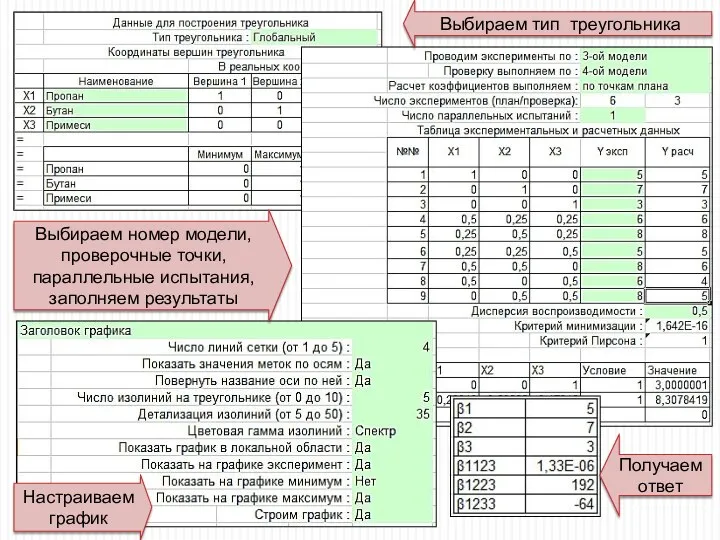
- 28. Выбираем тип треугольника Выбираем номер модели, проверочные точки, параллельные испытания, заполняем результаты Получаем ответ Настраиваем график
- 30. Скачать презентацию









 Треугольники. Задачи
Треугольники. Задачи Метод координат при решении стереометрических задач. Урок геометрии, 11 класс
Метод координат при решении стереометрических задач. Урок геометрии, 11 класс Трапеция. Теорема о средней линии трапеции
Трапеция. Теорема о средней линии трапеции Признаки делимости чисел на 2, 3, 9
Признаки делимости чисел на 2, 3, 9 Конус. Элементы конуса. Сечение конуса
Конус. Элементы конуса. Сечение конуса Координатная прямая
Координатная прямая Сложная функция. 10 класс
Сложная функция. 10 класс презентации и конспекты уроков
презентации и конспекты уроков Прогрессии вокруг нас. (9 класс)
Прогрессии вокруг нас. (9 класс) Число и цифра 4
Число и цифра 4 Презентация по математике тема: Часы, минуты, сутки (подготовительная группа)
Презентация по математике тема: Часы, минуты, сутки (подготовительная группа) Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Измерение углов
Измерение углов Цилиндр
Цилиндр Производная функции. Возрастание и убывание функций
Производная функции. Возрастание и убывание функций Интеллектуальная математическая игра для 6 класса
Интеллектуальная математическая игра для 6 класса Сложение и вычитание в пределах 20 2 класс УМК Школа 2100
Сложение и вычитание в пределах 20 2 класс УМК Школа 2100 Урок математики Движение с отставанием 4 класс Петерсон Л. Г.
Урок математики Движение с отставанием 4 класс Петерсон Л. Г. Численные методы
Численные методы Признаки параллельности прямых
Признаки параллельности прямых Квадратный корень. Арифметический квадратный корень
Квадратный корень. Арифметический квадратный корень Розкладання квадратного тричлена на множники
Розкладання квадратного тричлена на множники Площадь фигуры
Площадь фигуры Плоские фигуры - многоугольники. Объемные фигуры
Плоские фигуры - многоугольники. Объемные фигуры Функция. Область определения и область значений функции. 7 класс
Функция. Область определения и область значений функции. 7 класс Презентация к уроку математики Зимние забавы
Презентация к уроку математики Зимние забавы Линейная модель парной регрессии. Метод наименьших квадратов
Линейная модель парной регрессии. Метод наименьших квадратов Начальные геометрические сведения. Прямая и отрезок
Начальные геометрические сведения. Прямая и отрезок