Содержание
- 2. Дифференциальное уравнение в частных производных Системы ДУЧП
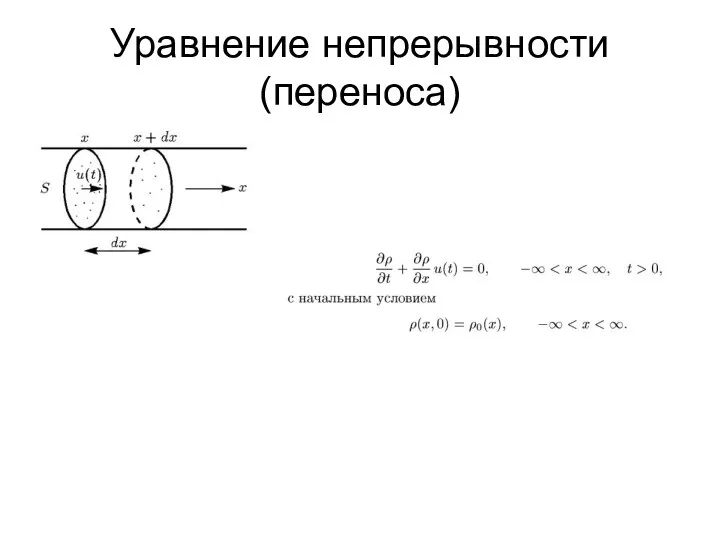
- 3. Уравнение непрерывности (переноса)
- 4. Уравнение непрерывности (переноса)
- 5. Уравнение переноса
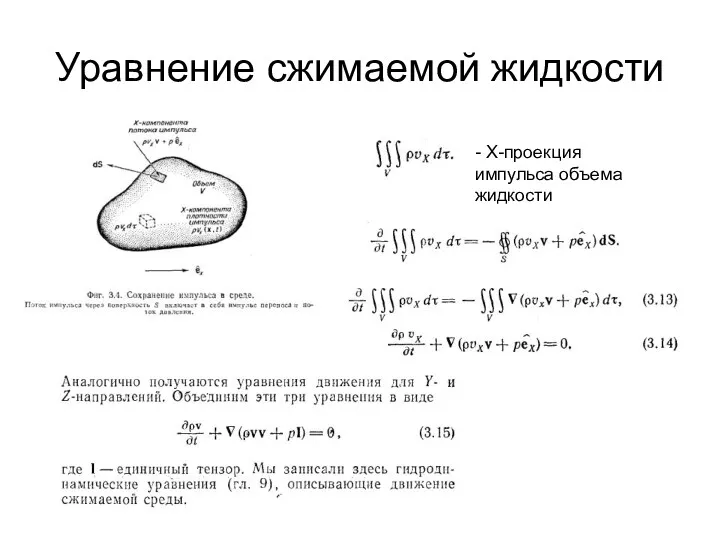
- 6. Уравнение сжимаемой жидкости - Х-проекция импульса объема жидкости
- 7. Уравнения классической гидродинамики уравнение состояния
- 8. Уравнение теплопроводности
- 9. Уравнения электромагнетизма
- 10. Консервативные ДУ
- 11. Уравнение диффузии
- 12. Волновое уравнение
- 13. Уравнение Пуассона и Лапласа
- 14. Классификация ДУЧП 2-го порядка
- 15. Аппроксимация производных конечными разностями
- 16. Граничные и начальные условия
- 17. Аппроксимация производных конечными разностями
- 18. Аппроксимация 1-го порядка точности
- 19. Аппроксимация 1-го порядка точности
- 20. Центральная аппроксимация 2-го порядка
- 21. Центральная аппроксимация 2-ой производной
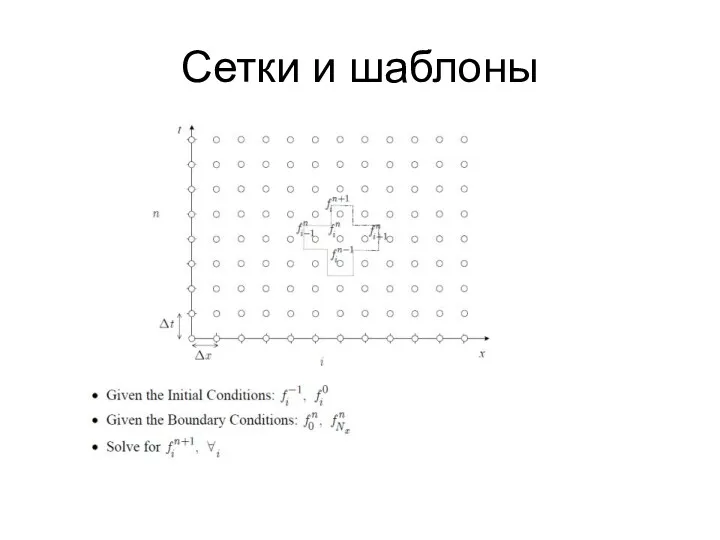
- 22. Сетки и шаблоны
- 23. Точность аппроксимации
- 24. Явные и неявные схемы
- 25. Методы составления схем Метод разностной аппроксимации Интегро-интерполяционный метод (законы сохранения) Метод неопределенных коэффициентов
- 26. Сходимость
- 27. Анализ устойчивости по методу Неймана Исследуется поведение Фурье-мод на сетке независимо друг от друга. Требуется устойчивость
- 28. Анализ устойчивости Матрица перехода может меняться по пространственной и временной сеткам – условие устойчивости должно выполняться
- 29. Анализ уравнения переноса
- 31. Схема Лакса
- 32. Дисперсия и диффузия на сетке Разностная схема Лакса соответствует ДУ с диффузионным членом (3), который компенсирует
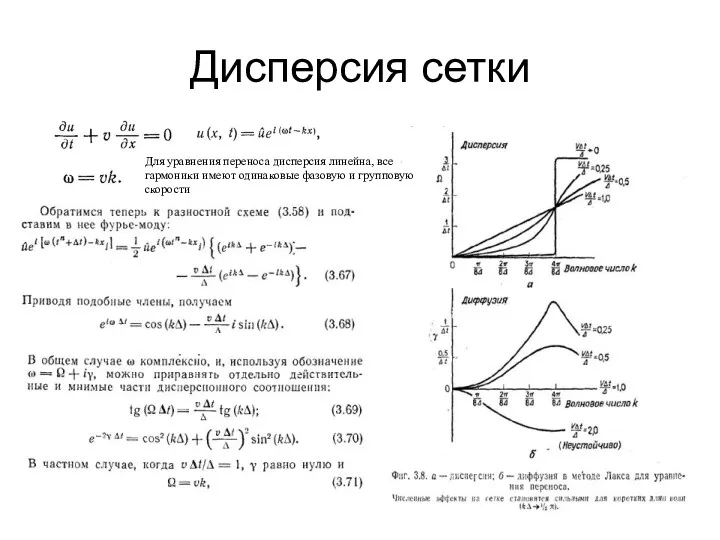
- 33. Дисперсия сетки Для уравнения переноса дисперсия линейна, все гармоники имеют одинаковые фазовую и групповую скорости
- 34. Дисперсия сетки для одномерного волнового уравнения Теперь рассмотрим дисперсию схемы
- 35. Дисперсия сетки для одномерного волнового уравнения Рассмотрим случай очень плотной сетки Рассмотрим случай
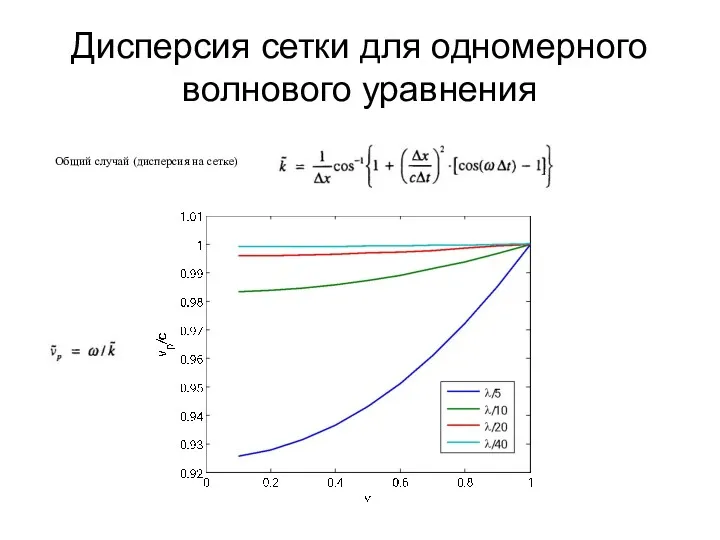
- 36. Дисперсия сетки для одномерного волнового уравнения Общий случай (дисперсия на сетке)
- 37. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)
- 38. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)
- 39. Устойчивость метода Лакса-Вендрофа
- 40. Диффузия в схеме Лакса-Вендрофа
- 41. Условие устойчивости в многомерных задачах гиперболического типа Метод Лакса
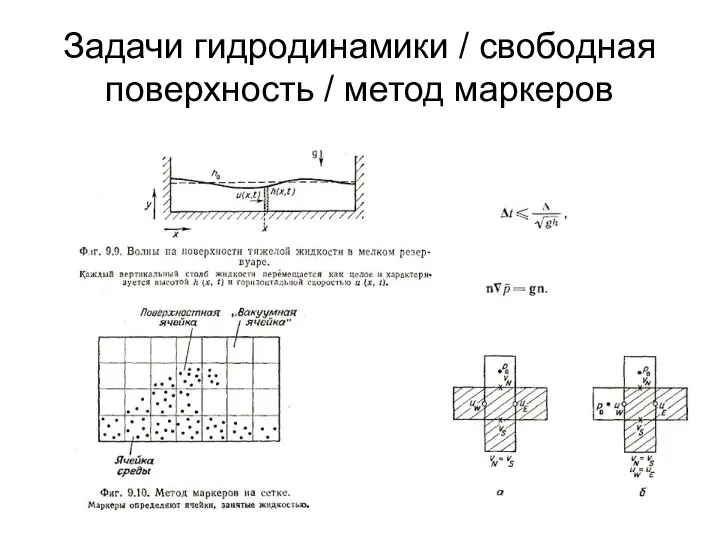
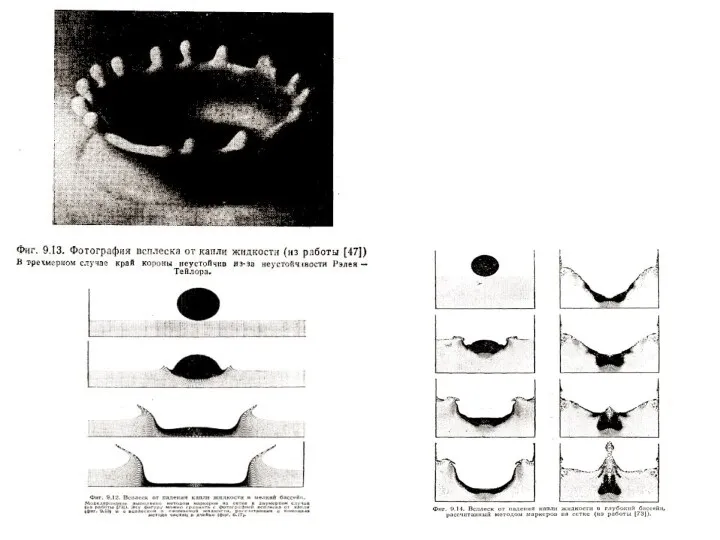
- 42. Задачи гидродинамики / свободная поверхность / метод маркеров
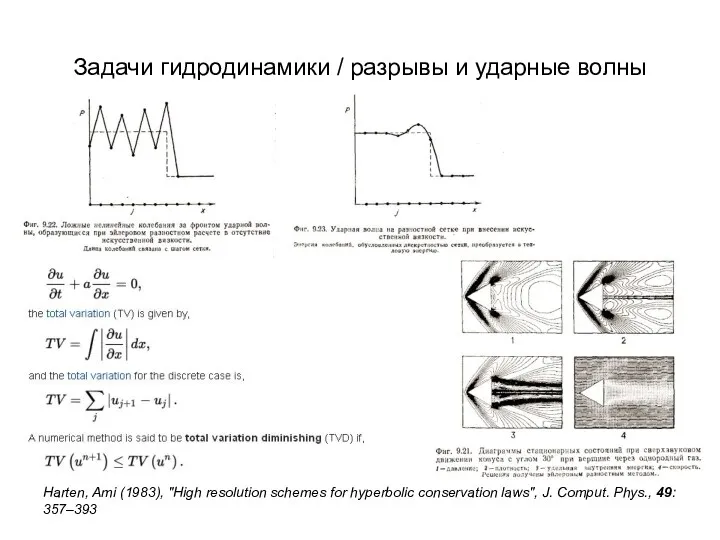
- 45. Задачи гидродинамики / разрывы и ударные волны Harten, Ami (1983), "High resolution schemes for hyperbolic conservation
- 46. Консервативные схемы
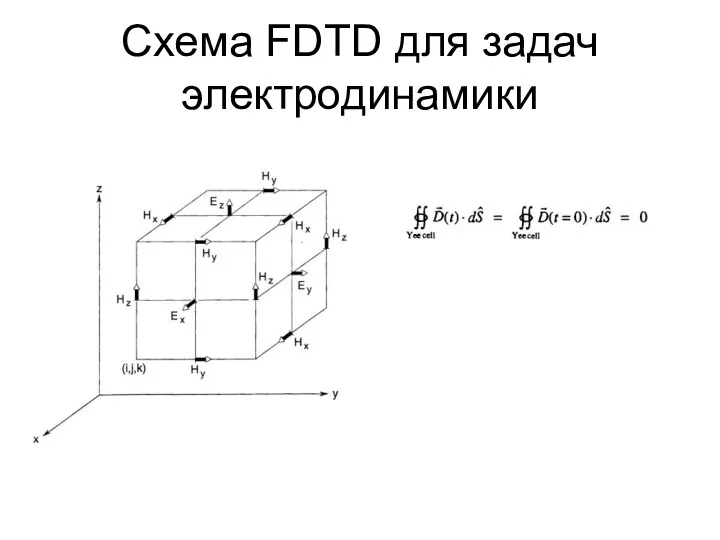
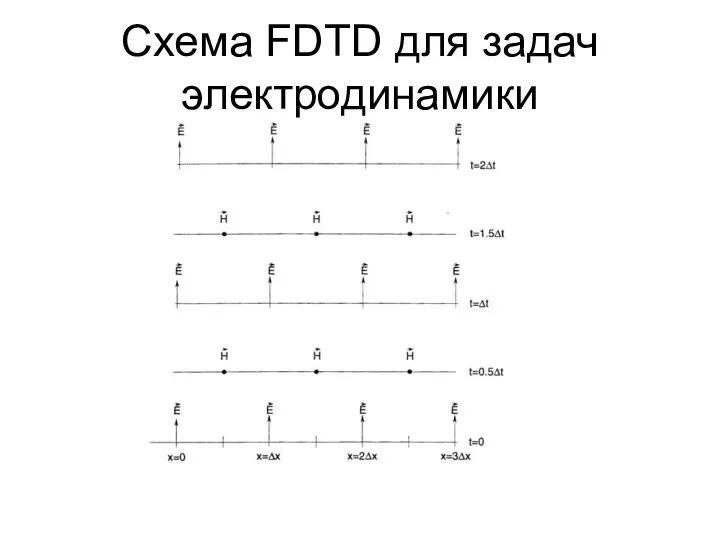
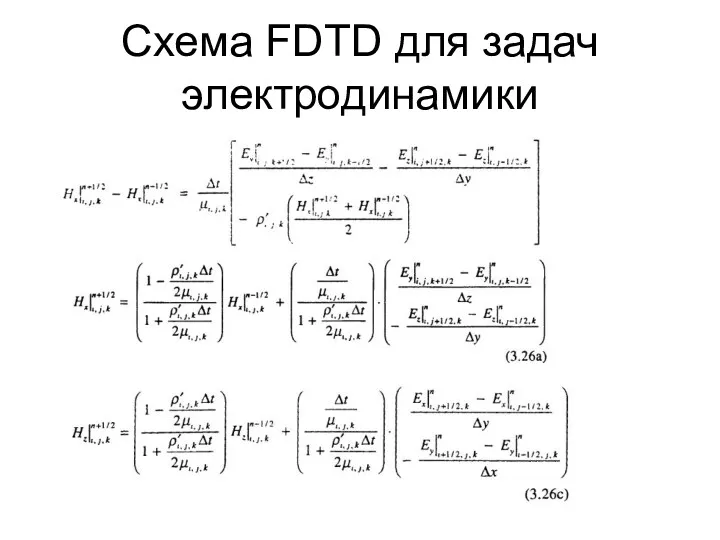
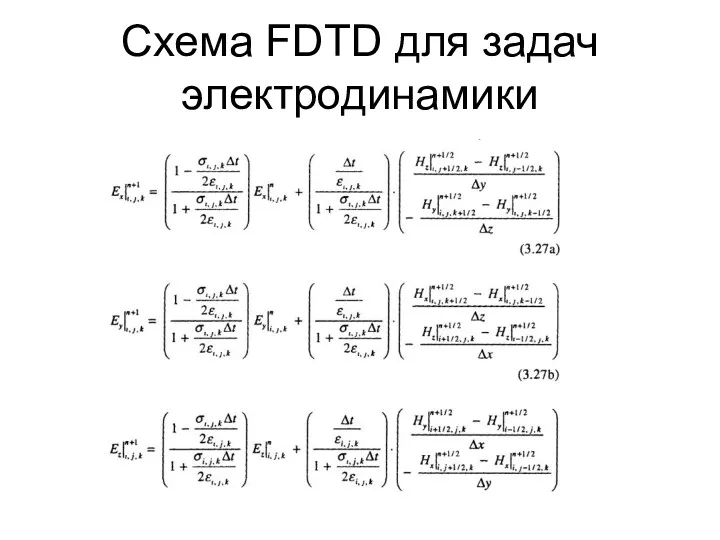
- 47. Схема FDTD для задач электродинамики
- 48. Схема FDTD для задач электродинамики
- 49. Схема FDTD для задач электродинамики
- 50. Схема FDTD для задач электродинамики
- 51. Схема FDTD для задач электродинамики
- 52. Схема FDTD для задач электродинамики
- 53. Схема FDTD для задач электродинамики
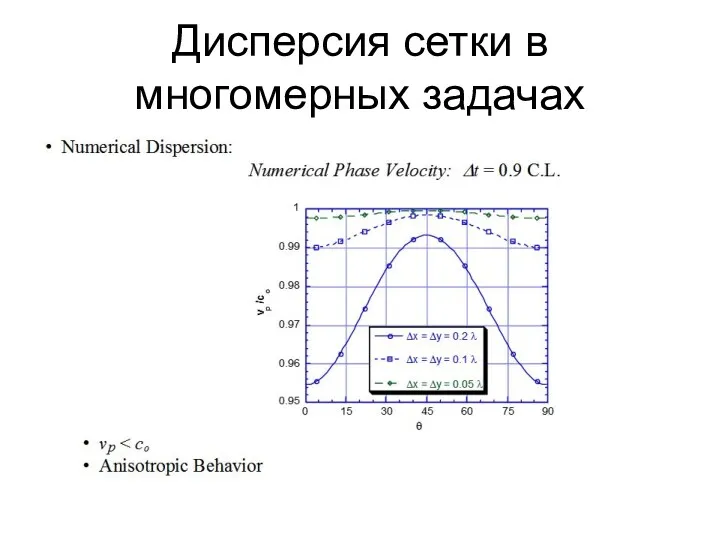
- 54. Дисперсия сетки в многомерных задачах
- 56. Скачать презентацию








































 Методы решения текстовых задач
Методы решения текстовых задач Устные задачи на готовых чертежах. Смежные и вертикальные углы
Устные задачи на готовых чертежах. Смежные и вертикальные углы Формулы сокращенного умножения. Путешествие По стране формул
Формулы сокращенного умножения. Путешествие По стране формул Комбинаторика. Теория вероятности
Комбинаторика. Теория вероятности Умножение десятичных дробей. Тренажер
Умножение десятичных дробей. Тренажер Mixed strategy Nash equilibrium. (Lecture 3)
Mixed strategy Nash equilibrium. (Lecture 3) Относительная частота случайного события. Интегрированный урок в 9 классе математика + английский язык
Относительная частота случайного события. Интегрированный урок в 9 классе математика + английский язык Сложение и вычитание чисел
Сложение и вычитание чисел Математические модели и математическое моделирование
Математические модели и математическое моделирование Свойства производной. Построение графиков функций
Свойства производной. Построение графиков функций Квадратный трехчлен. 8 класс
Квадратный трехчлен. 8 класс Ықтималдықтар теориясының негіздері
Ықтималдықтар теориясының негіздері Математический брейн-ринг для учащихся 5 класса
Математический брейн-ринг для учащихся 5 класса Конспект урока математики в 3 классе Истомина
Конспект урока математики в 3 классе Истомина Осевая и центральная симметрии
Осевая и центральная симметрии Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Решение рациональных уравнений
Решение рациональных уравнений Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Весёлый счёт.
Весёлый счёт. Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа).
Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа). Дисперсионный анализ ANOVA (продолжение). Занятие 4
Дисперсионный анализ ANOVA (продолжение). Занятие 4 Метрология — наука об измерениях, методах и средствах обеспечения их единства
Метрология — наука об измерениях, методах и средствах обеспечения их единства Додавання і віднімання числа частинами
Додавання і віднімання числа частинами Метрология. Научные изыскания в области метрологии
Метрология. Научные изыскания в области метрологии Пропорции
Пропорции Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Дополнительные возможности анализа данных в MS Excel. Аппроксимация экспериментальных данных. Линии тренда
Дополнительные возможности анализа данных в MS Excel. Аппроксимация экспериментальных данных. Линии тренда Решение задач с помощью дробных рациональных уравнений
Решение задач с помощью дробных рациональных уравнений