Содержание
- 2. 1.Задача об использовании ресурсов Задача 1. Предприятие производит изделия двух типов A и B из трех
- 3. (2.1) По смыслу задачи (2.2) Прибыль предприятия при плане x1, x2 равна (2.3) Необходимо найти значения
- 4. Условию (2.2) удовлетворяют точки первой четверти. Для получения полуплоскостей, соответствующих неравенствам системы (2.1), построим их границы,
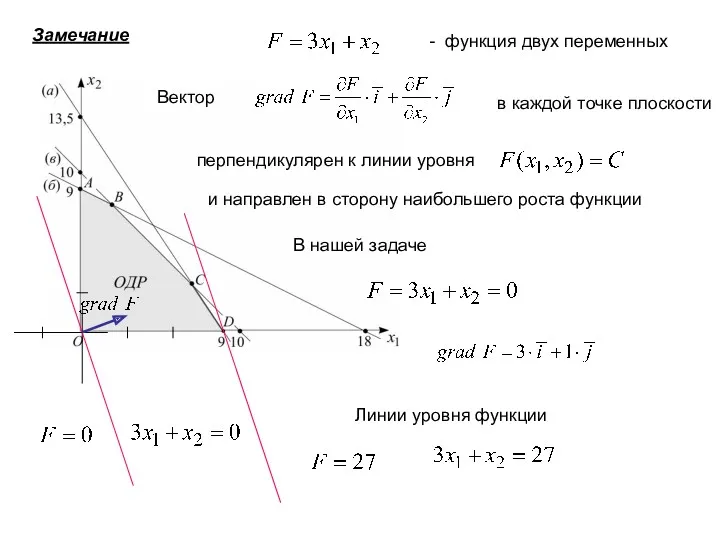
- 5. Замечание - функция двух переменных Вектор в каждой точке плоскости перпендикулярен к линии уровня и направлен
- 6. В ы в о д: предприятию выгодно выпустить только 9 изделий типа А и не выпускать
- 7. Структура целевой функции позволяет утверждать, что ее значения могут быть увеличены за счет увеличения значений как
- 8. В результате новыми базисными переменными стали x1, x4, x5, а новыми свободными - x3, x2. Выражаем
- 9. Полагаем свободные переменные Тогда базисные переменные согласно системе (2.5') принимают значения x1=9 , x4=9, x5=1, т.е.
- 10. 4.Транспортная задача. Экономико-математическая модель задачи Задача. Поставщики А1, А2, А3 имеют некоторую продукцию в количествах а1=100,
- 11. Пусть xij - объем перевозки от i -го поставщика к j -у потребителю Мощности поставщиков должны
- 12. Математическая формулировка задачи На множестве неотрицательных решений системы уравнений (2.7)-(2.8) найти такое решение при котором функция
- 13. Составим первый план перевозок. В этом плане отличными от нуля перевозками могут быть лишь m+n-1=3+4-1=6 значений
- 14. На втором шаге заполняем клетку (33) x33=100, т.к. C33=3 − наименьшее, значением . При этом вычеркивается
- 15. Для проверки оптимальности полученного плана воспользуемся методом потенциалов. Введём строку потенциалов Uj и столбец потенциалов Vi
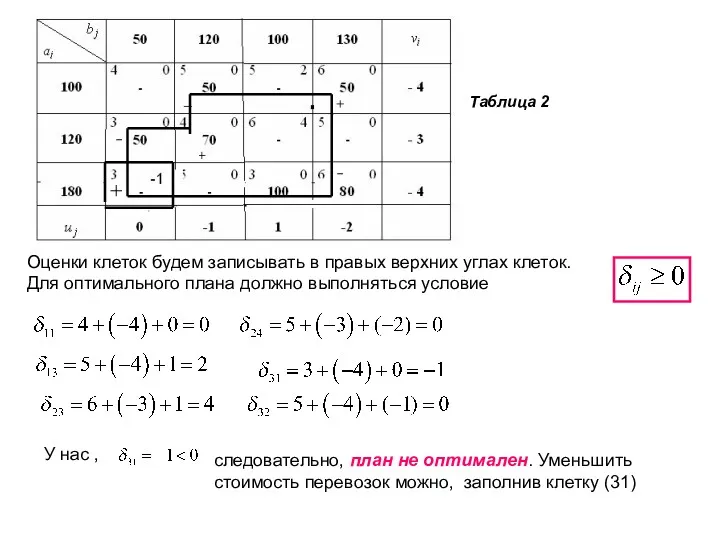
- 16. Оценки клеток будем записывать в правых верхних углах клеток. Для оптимального плана должно выполняться условие У
- 17. (на каждой единице, проставленной в клетку (31), стоимость перевозок уменьшится на 1 ден. ед.). Для заполнения
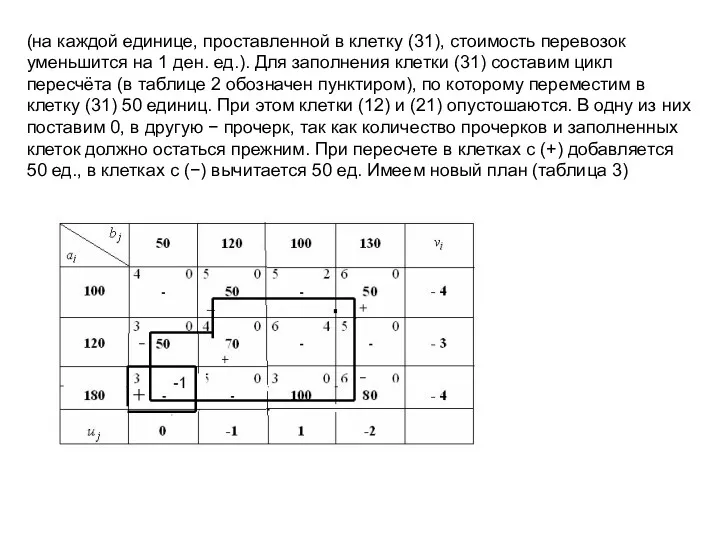
- 18. Уменьшить стоимость перевозок можно, заполнив клетку (31) (на каждой единице, проставленной в клетку (31), стоимость перевозок
- 19. Имеем новый план (таблица 3). Найдём для него потенциалы и вычислим Составим цикл для клетки (24).
- 20. Так как , то составим цикл для клетки (24). В этом цикле перемещается 0 единиц (фактически
- 22. Скачать презентацию
















 Интегрирование функций комплексной переменной
Интегрирование функций комплексной переменной Однородная система линейных алгебраических уравнений. Фундаментальная система решений
Однородная система линейных алгебраических уравнений. Фундаментальная система решений Прямая и отрезок
Прямая и отрезок Неравенства с модулем. Способы решения неравенств с модулями
Неравенства с модулем. Способы решения неравенств с модулями Тренажёр У кого Карлсон в гостях?
Тренажёр У кого Карлсон в гостях? 1нче сыйныфта 1санын алу темасына дәрескә презентация
1нче сыйныфта 1санын алу темасына дәрескә презентация Конспект и презентация к интегрированному уроку (математика+экология) 4 класс Закрепление вычислительных навыков в пределах миллиона
Конспект и презентация к интегрированному уроку (математика+экология) 4 класс Закрепление вычислительных навыков в пределах миллиона Сравнение, сложение и вычитание дробей с разными знаменателями. 6 класс
Сравнение, сложение и вычитание дробей с разными знаменателями. 6 класс Формальные теории и исчисления. Модуль 3
Формальные теории и исчисления. Модуль 3 Непрерывная случайная величина. Равномерное, показательное и нормальное распределение
Непрерывная случайная величина. Равномерное, показательное и нормальное распределение Комбинаторика. Задачи
Комбинаторика. Задачи Метр — одиниця довжини
Метр — одиниця довжини Причины использования измерений в любой науке, использующей статистические методы
Причины использования измерений в любой науке, использующей статистические методы Своя игра по математике для старшекласников
Своя игра по математике для старшекласников Умножение и деление дробей
Умножение и деление дробей Транспортные задачи
Транспортные задачи История комплексных чисел от Кардано до Гамильтона
История комплексных чисел от Кардано до Гамильтона Логарифмы. Определение логарифма. Основное логарифмическое тождество
Логарифмы. Определение логарифма. Основное логарифмическое тождество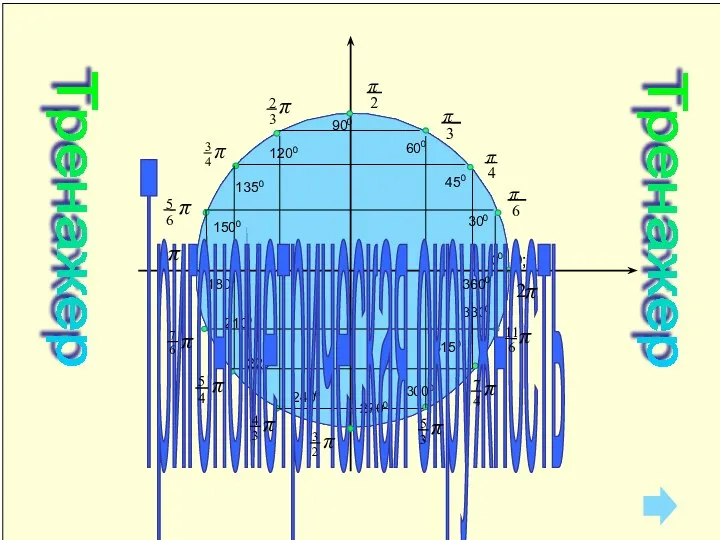 Поворот точек. Тригонометрическая окружность
Поворот точек. Тригонометрическая окружность Единицы длины. Километр. Соотношение единиц длины
Единицы длины. Километр. Соотношение единиц длины Сложение и вычитание смешанных чисел. Разработка технологической карты по математике 5 класса
Сложение и вычитание смешанных чисел. Разработка технологической карты по математике 5 класса Объемы тел
Объемы тел Решение показательных уравнений методом введения новой переменной
Решение показательных уравнений методом введения новой переменной Розв’язання вправ. Квадратне рівняння
Розв’язання вправ. Квадратне рівняння Комбинаторные задачи. Комбинаторика. Расположение перестановки n! выбор n!
Комбинаторные задачи. Комбинаторика. Расположение перестановки n! выбор n! Состав числа 10
Состав числа 10 Логическое мышление, его развитие при обучении математике
Логическое мышление, его развитие при обучении математике Квадратичная функция. Её свойства и график. Обобщающий урок
Квадратичная функция. Её свойства и график. Обобщающий урок