Содержание
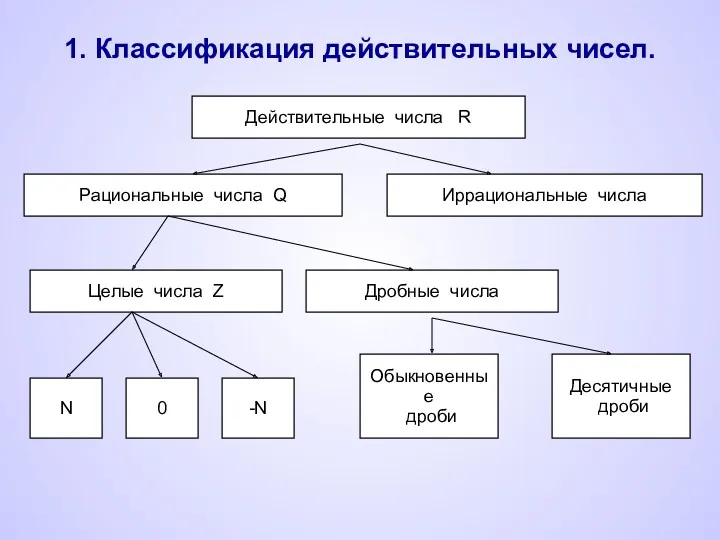
- 2. 1. Классификация действительных чисел. Действительные числа R Рациональные числа Q Иррациональные числа Дробные числа Целые числа
- 3. 2. Натуральные числа. Деление с остатком.
- 5. 3. Признаки делимости натуральных чисел Натуральное число n делится на натуральное число р, равное 1) 2,
- 6. 3. Признаки делимости натуральных чисел Пример: 2: 264; 37860 5: 379800; 4675 10: 3786300 4 (25):
- 7. 4. НОК и НОД натуральных чисел.
- 8. 7
- 10. 5. Взаимно простые числа.
- 11. 6. Основная теорема арифметики. Теорема: Любое составное число можно представить в виде произведения простых множителей и
- 12. 7. Делимость суммы и произведения.
- 13. 8. Свойства, связанные с последовательным расположением натуральных чисел. Одно из n последовательных целых чисел делится на
- 14. 9. Целые числа. Определение. Целые числа – натуральные числа, числа противоположные натуральным и нуль. Многие свойства
- 15. 10. Дробные числа.
- 16. 10. Дробные числа.
- 18. Скачать презентацию














 Образование чисел из одного десятка и нескольких единиц. 1 класс
Образование чисел из одного десятка и нескольких единиц. 1 класс НОД по математическому развитию в подготовительной группе.
НОД по математическому развитию в подготовительной группе. Количественные характеристики случайных переменных
Количественные характеристики случайных переменных Описательная статистика
Описательная статистика Геометрические задачи типа 18
Геометрические задачи типа 18 презентация Веселая неделя
презентация Веселая неделя Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Конспект урока математики на тему: Сложение и вычитание в пределах 20.
Конспект урока математики на тему: Сложение и вычитание в пределах 20. Математическая игра. Счастливый случай. 7 класс
Математическая игра. Счастливый случай. 7 класс Сумматор
Сумматор Решение задач на смеси и сплавы
Решение задач на смеси и сплавы Математическое моделирование как способ решения текстовой задачи
Математическое моделирование как способ решения текстовой задачи Показательные уравнения и неравенства
Показательные уравнения и неравенства Алгоритм сложения чисел с переходом через десяток
Алгоритм сложения чисел с переходом через десяток Логические универсальные учебные действия на уроках математики. 7 класс
Логические универсальные учебные действия на уроках математики. 7 класс Вычитание вида 14 -
Вычитание вида 14 - Теорема Пифагора. Теорема в стихах
Теорема Пифагора. Теорема в стихах презентация по математика на тему Сколько?
презентация по математика на тему Сколько? Готовимся к ГИА, 9 класс. Тест 1, часть 1
Готовимся к ГИА, 9 класс. Тест 1, часть 1 Тригонометричні функції суми та різниці двох кутів, подвійного аргументу. Сума та різниця синусів і косинусів. Лекція №13
Тригонометричні функції суми та різниці двох кутів, подвійного аргументу. Сума та різниця синусів і косинусів. Лекція №13 Производные и дифференциалы высших порядков
Производные и дифференциалы высших порядков Приближенное вычисление интегралов
Приближенное вычисление интегралов Описанная окружность
Описанная окружность Презентация совместной образовательной деятельности воспитателя и воспитанников по теме:Развитие познавательной и исследовательской деятельности в математических играх
Презентация совместной образовательной деятельности воспитателя и воспитанников по теме:Развитие познавательной и исследовательской деятельности в математических играх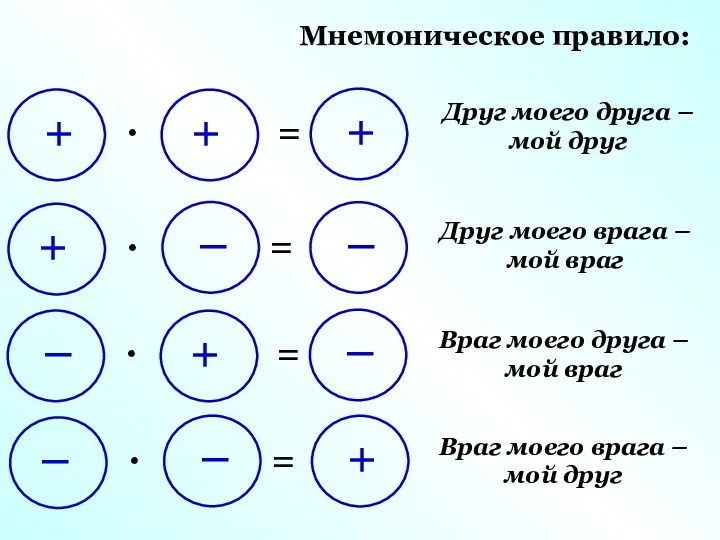 Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел Параллелограмм. Свойства параллелограмма
Параллелограмм. Свойства параллелограмма Арифметические операции и их свойства.
Арифметические операции и их свойства. Симметрия вокруг нас
Симметрия вокруг нас