Содержание
- 2. Характеристическая функция Пусть U — так называемое универсальное множество, из элементов которого образованы все остальные множества,
- 3. Функция принадлежности Нечеткие множества есть естественное обобщение обычных множеств, когда мы отказываемся от бинарного характера этой
- 4. Нечеткое множество Более строго, нечетким множеством A называется совокупность пар A={ | x∈U}, где μA —
- 5. Пример U={a, b, c, d, e} A={ , , , , } a не принадлежит множеству
- 6. Лингвистическая переменная Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или
- 7. Пример Лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый"
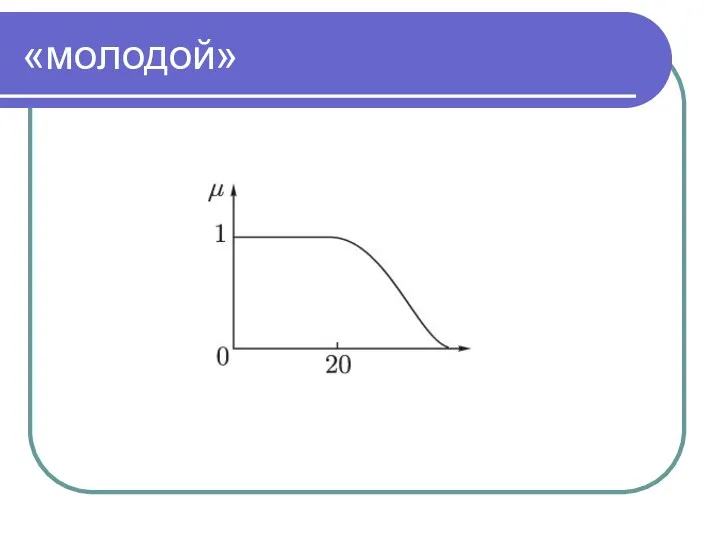
- 8. «молодой»
- 9. Терм-множество Терм–множеством (term set) называется множество всех возможных значений лингвистической переменной. Термом (term) называется любой элемент
- 10. Пример Рассмотрим переменную “скорость автомобиля”, которая оценивается по шкале “низкая", "средняя", "высокая” и “очень высокая". В
- 11. Строгое определение Лингвистическая переменная задается пятеркой (x, T, U, G, M), где x - имя переменной;
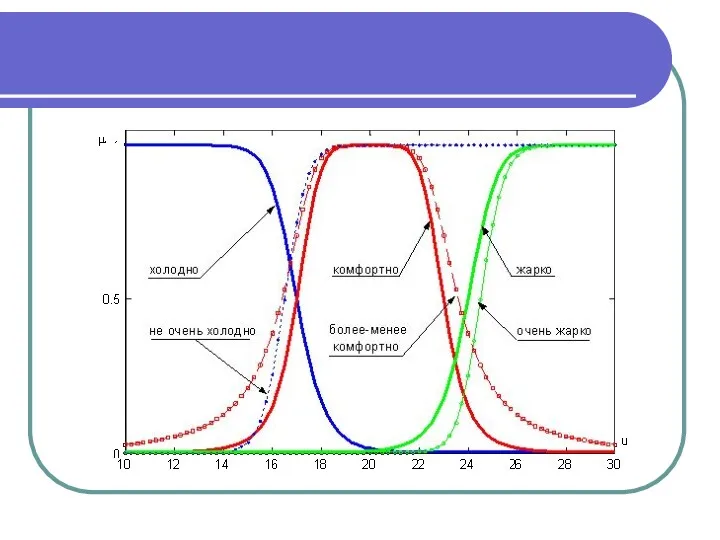
- 12. Пример Рассмотрим лингвистическую переменную с именем x= "температура в комнате". Тогда оставшуюся четверку (T, U, G,
- 13. Пример синтаксические правила G, порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее"; семантические правила
- 15. Носитель и высота Носителем (суппортом) нечеткого множества A называется четкое множество supp A таких точек в
- 16. Нормальное нечеткое множество Нечеткое множество A называется нормальным, если В противном случае оно называется субнормальным. Нечеткое
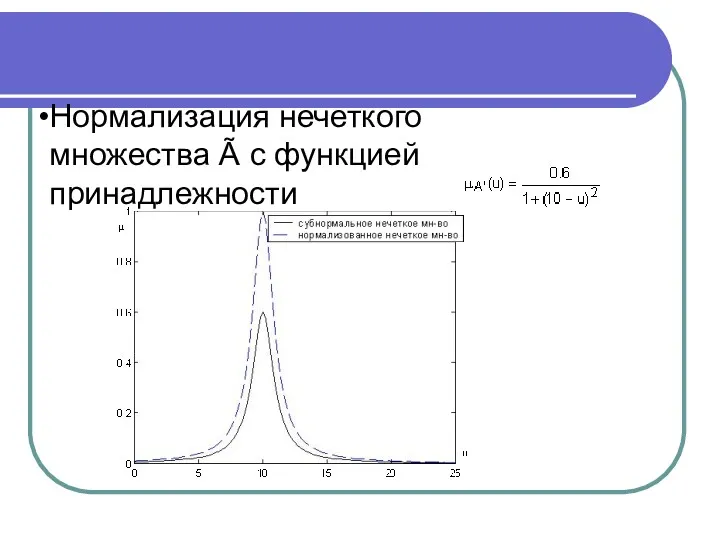
- 17. Непустое субнормальное нечеткое множество можно привести к нормальному (нормализовать) по формуле
- 18. Нормализация нечеткого множества Ã с функцией принадлежности .
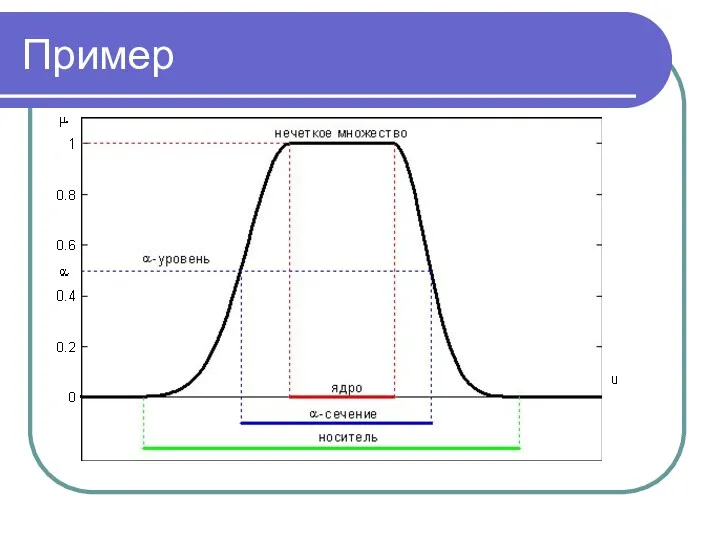
- 19. Ядро Ядром нечеткого множества Ã называется четкое подмножество универсального множества U, элементы которого имеют степени принадлежности
- 20. Срез Множеством уровня α (α-срезом, α-сечением) нечеткого множества A называется четкое подмножество универсального множества U, определяемое
- 21. Пример
- 22. Точка перехода Множество строгого уровня определяется в виде Aα={x| μA(x)>α}. В частности, носителем нечеткого множества является
- 23. Четкое множество Четкое множество A*, ближайшее к нечеткому множеству A, определяется следующим образом:
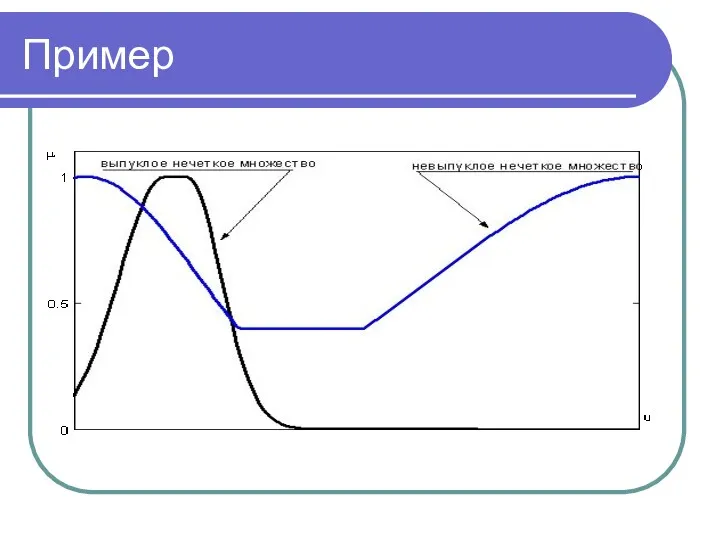
- 24. Выпуклое множество Нечеткое множество A в пространстве U=Rn называется выпуклым нечетким множеством тогда и только тогда,
- 25. Пример
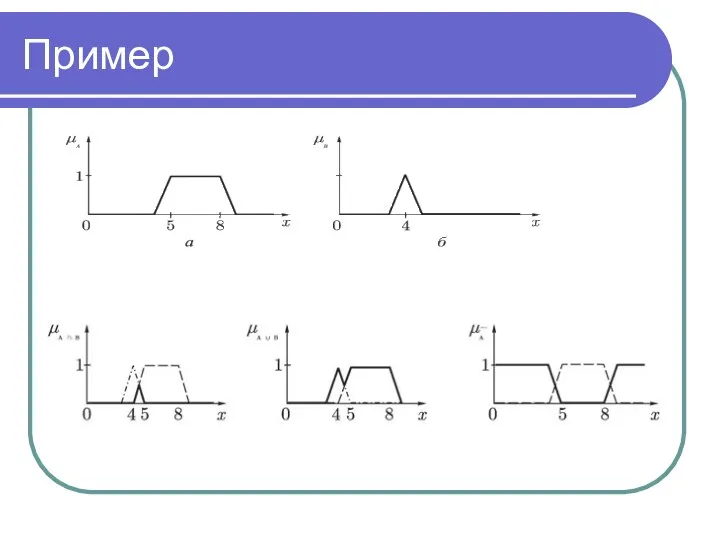
- 26. Операции Объединение μA∪B(x)=max{μA(x), μB(x)} Пересечение μA∩B(x)=min{μA(x), μB(x)} Дополнение
- 27. Пример
- 28. Треугольная норма Треугольной нормой (t-нормой) называется бинарная операция T на единичном интервале [0,1]×[0,1]→[0,1] , удовлетворяющая следующим
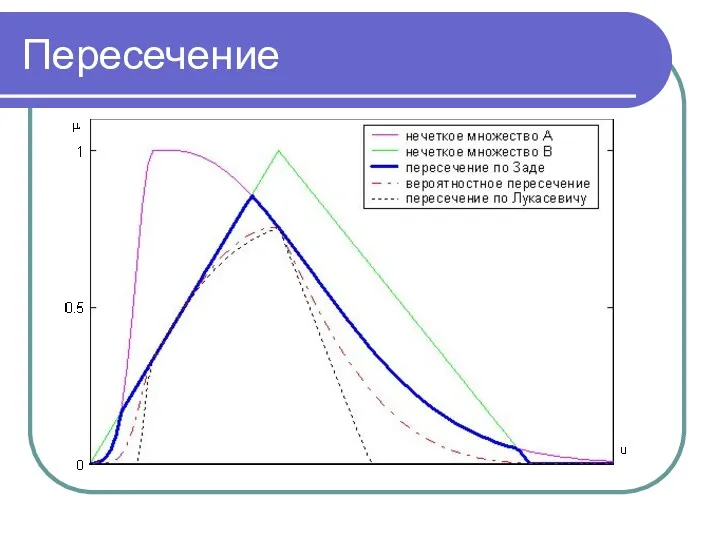
- 29. Пересечение
- 30. Треугольная конорма Треугольной конормой (s-нормой) называется бинарная операция S на единичном интервале [0,1]×[0,1]→[0,1] , удовлетворяющая следующим
- 32. Скачать презентацию






















 Устный счет по математике
Устный счет по математике Решение задач на движение (навстречу и вдогонку)
Решение задач на движение (навстречу и вдогонку) Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Конспект урока по математике в 1 классе
Конспект урока по математике в 1 классе Презентация к уроку математики Прямой и обратный порядок Диск
Презентация к уроку математики Прямой и обратный порядок Диск Методы непараметрического спектрального анализа. Основные показатели качества оценок СПМ
Методы непараметрического спектрального анализа. Основные показатели качества оценок СПМ Материал на конкурс Лучшая разработка урока математики.
Материал на конкурс Лучшая разработка урока математики. Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации
Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации Быстрый счёт
Быстрый счёт Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Распределительное свойство умножения
Распределительное свойство умножения Цилиндр. Решение задач
Цилиндр. Решение задач Время и его измерение
Время и его измерение Урок Математики в 1 классе УМК Школа России Тема Закрепление сложения и вычитания в пределах 10
Урок Математики в 1 классе УМК Школа России Тема Закрепление сложения и вычитания в пределах 10 Вычитание из 8 и 9. Нахождение неизвестного слагаемого
Вычитание из 8 и 9. Нахождение неизвестного слагаемого Сокращенные таблицы истинности
Сокращенные таблицы истинности Математика - царица всех наук
Математика - царица всех наук Повторение курса геометрии 8 класса. Задачи на готовых чертежах
Повторение курса геометрии 8 класса. Задачи на готовых чертежах Начертательная геометрия
Начертательная геометрия Взаимно обратные числа (часть 2)
Взаимно обратные числа (часть 2) Метод дерева решений
Метод дерева решений Познавательные математические цепочки
Познавательные математические цепочки Осевая и центральная симметрия
Осевая и центральная симметрия Презентация по математическому развитию по программе Детство
Презентация по математическому развитию по программе Детство Углы и многоугольники. 5 класс
Углы и многоугольники. 5 класс Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Производная функции. Производная линейной функции
Производная функции. Производная линейной функции Расчет количества материала необходимого для ремонта
Расчет количества материала необходимого для ремонта