Содержание
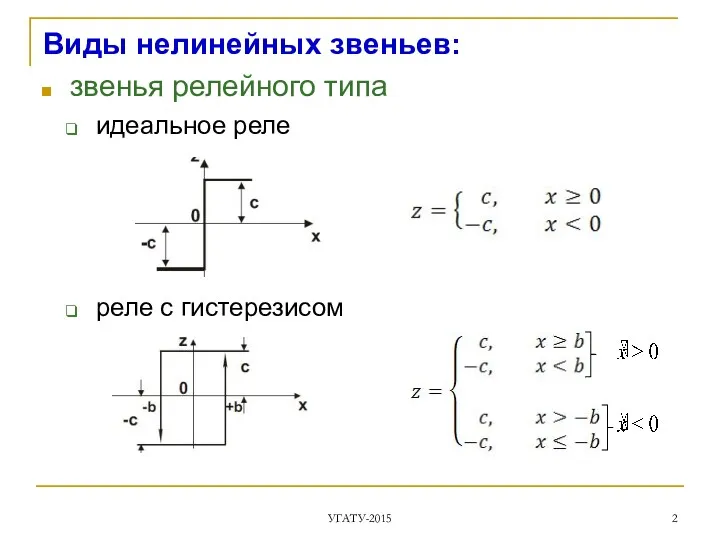
- 2. Виды нелинейных звеньев: звенья релейного типа идеальное реле реле с гистерезисом УГАТУ-2015
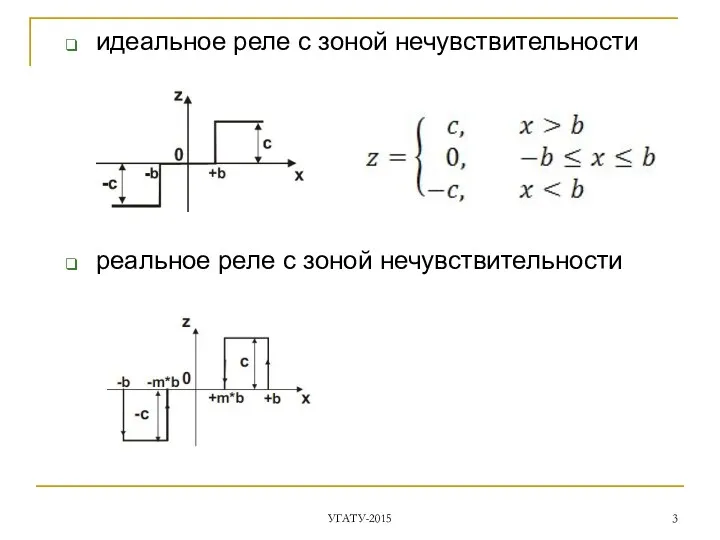
- 3. идеальное реле с зоной нечувствительности реальное реле с зоной нечувствительности УГАТУ-2015
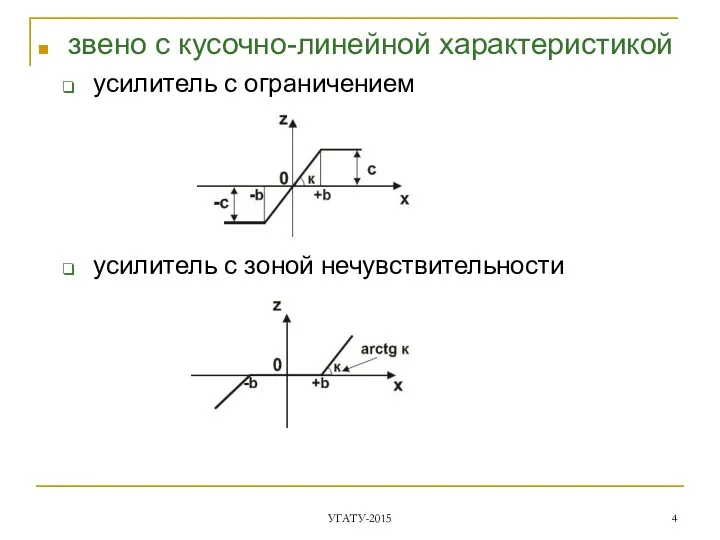
- 4. звено с кусочно-линейной характеристикой усилитель с ограничением усилитель с зоной нечувствительности УГАТУ-2015
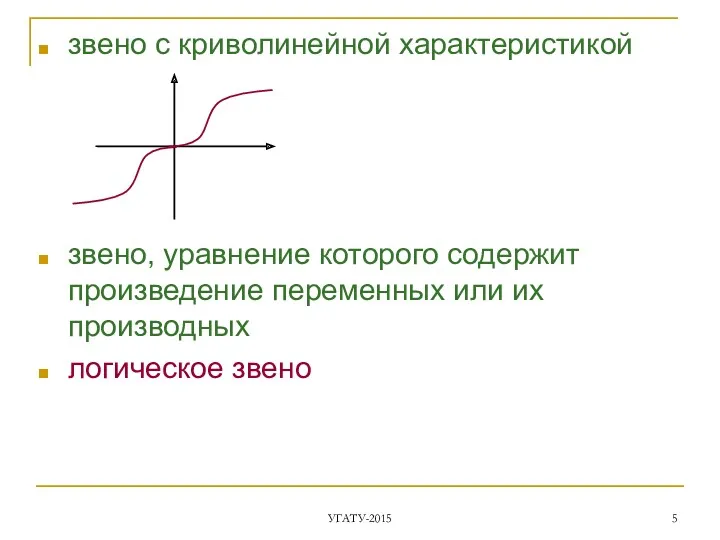
- 5. звено с криволинейной характеристикой звено, уравнение которого содержит произведение переменных или их производных логическое звено УГАТУ-2015
- 6. Метод гармонической линеаризации относится к приближенным методам прост и универсален широко распространен в инженерной практике УГАТУ-2015
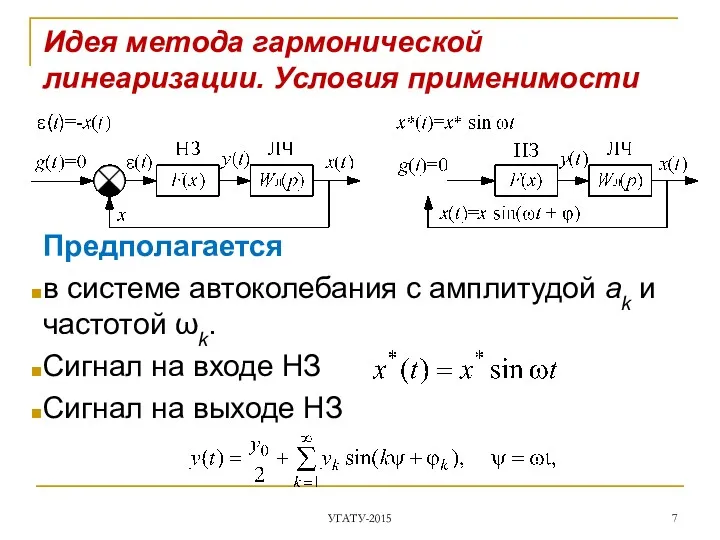
- 7. Идея метода гармонической линеаризации. Условия применимости Предполагается в системе автоколебания с амплитудой ak и частотой ωk.
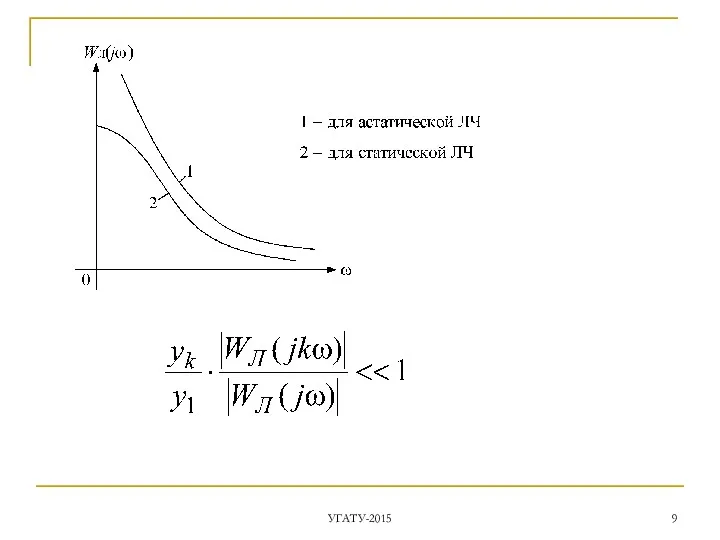
- 8. предполагается, что сигнал y(t), пройдя через линейную часть WЛ(jω), фильтруется ею в такой степени, что в
- 9. УГАТУ-2015
- 10. УГАТУ-2015 - уравнение баланса амплитуд - уравнение баланса фаз гармонических колебаний уравнения гармонического баланса (1) (2)
- 11. Решаются две группы задач: исследование периодических движений в нелинейных замкнутых системах (определение условий устойчивости и параметров
- 12. Гармоническая линеаризация нелинейностей Пусть заданная нелинейная функция При выполнении гипотезы фильтра переменная x(t) = a⋅sinωt =
- 13. Предполагаем где p=d/dt где q(a) и q'(a) – коэффициенты гармонической линеаризации УГАТУ-2015
- 14. Для однозначной нелинейной характеристики F(x) коэффициент q'(a)=0. Для неоднозначной характеристики типа гистерезис q'(a)≠0 и q'(a) УГАТУ-2015
- 15. Замена исходного нелинейного уравнения приближенным уравнением для первой гармоники называется гармонической линеаризацией передаточной функцией нелинейного гармонически
- 16. Исследование устойчивости периодических движений методом гармонической линеаризации Запишем уравнение замкнутой гармонически линеаризованной нелинейной САУ в операторной
- 17. Характеристическое уравнение гармонически линеаризованной нелинейной САУ: подставим в L(s) s=jωп выделим вещественную U(aп,ωп,) и мнимую V(aп,ωп)
- 18. определяются параметры ПД aп и ωп. УГАТУ-2015
- 19. Если при положительном приращении амплитуды ∆a>0 кривая Михайлова займет положение 1-1, а при отрицательном приращении амплитуды
- 20. Частотный метод исследования устойчивости ПД в НС Л. С. Голдфарба (1946 г.) Основная идея WН(a) −
- 21. s=jω решим полученное уравнение относительно неизвестных aп и ωп . Графоаналитическое решение - инверсный коэффициент гармонической
- 22. УГАТУ-2015 q q’
- 23. УГАТУ-2015
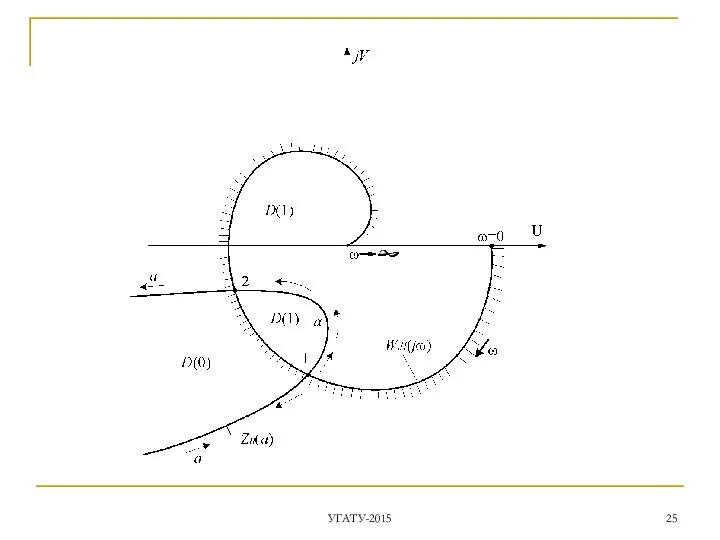
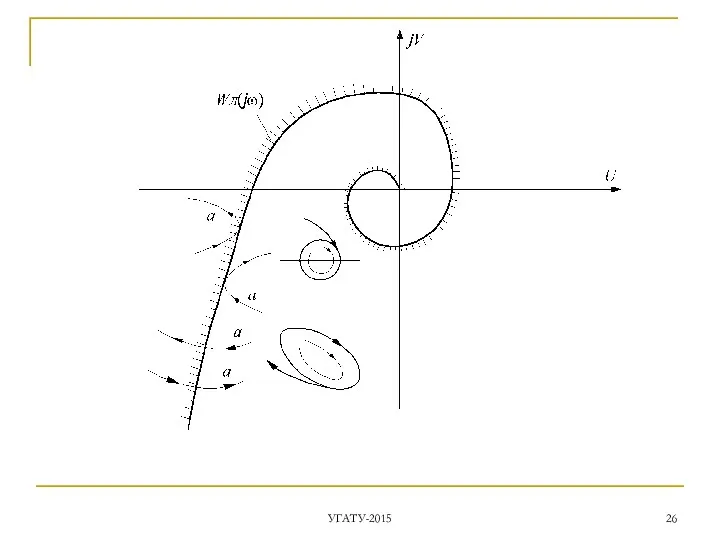
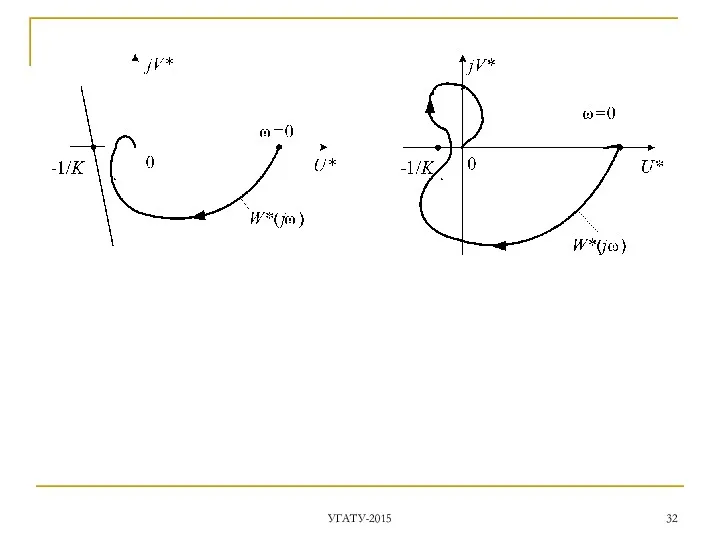
- 24. Оба годографа и строятся на одной комплексной плоскости. - АФХ линейной части определяет частоту ωп ПД,
- 25. УГАТУ-2015
- 26. УГАТУ-2015
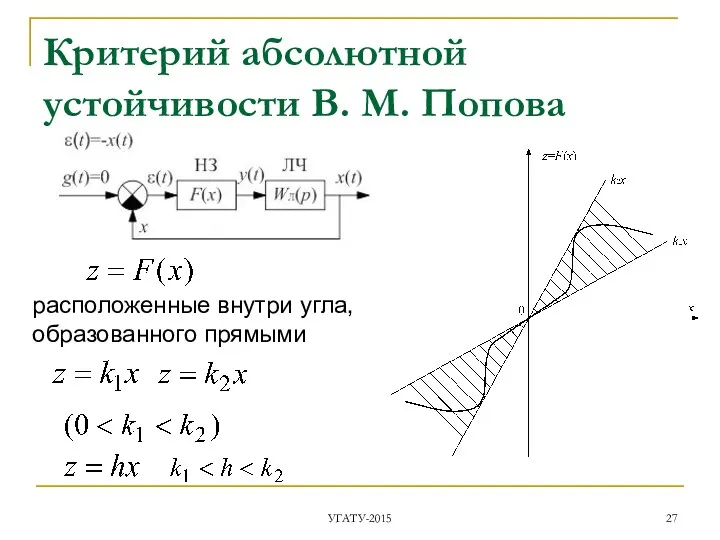
- 27. Критерий абсолютной устойчивости В. М. Попова УГАТУ-2015 расположенные внутри угла, образованного прямыми
- 28. линейная часть системы устойчива Абсолютная устойчивость нелинейной САУ предложена в 1959 г. в работе румынского математика
- 29. Теорема. Если замкнутая система состоит из устойчивой линейной части с передаточной функцией, все полюсы которой располагаются
- 30. Геометрическая интерпретация теоремы. введем видоизмененную частотную характеристику обозначим (2) (3) (4) УГАТУ-2015
- 31. (4) определяет собой прямую линию на плоскости , которая проходит через точку с координатами с угловым
- 32. УГАТУ-2015
- 33. Второй метод Ляпунова не требует нахождения решения дифференциального уравнения основная идея замена анализа решений нелинейных уравнений
- 34. исследуется изменение «расстояния» в пространстве состояний от текущей точки системы до начала координат В качестве оценки
- 35. Суть второго метода Ляпунова сводится к оценке изменения некоторой функции координат состояния системы вдоль траекторий движения
- 36. УГАТУ-2015 а б Рис. 1. Изменение функции V в случае устойчивой (а) и неустойчивой (б) систем
- 37. УГАТУ-2015 Полной производной функции Ляпунова в силу системы называется функция – вектор-строка частных производных. в развернутой
- 38. Теоремы второго метода Ляпунова Состояние равновесия системы является асимптотически устойчивым, если для положительно определенной функции Ляпунова
- 39. Теорема о неустойчивости Состояние равновесия системы является неустойчивым, если для положительно определенной функции Ляпунова V(x) ее
- 40. Пример с помощью второго метода Ляпунова оценить устойчивость системы, поведение которой описывают следующие уравнения: Полагаем u
- 41. Выберем для нее в качестве функции Ляпунова следующую функцию: Определим теперь полную производную функции Ляпунова вдоль
- 43. Скачать презентацию






























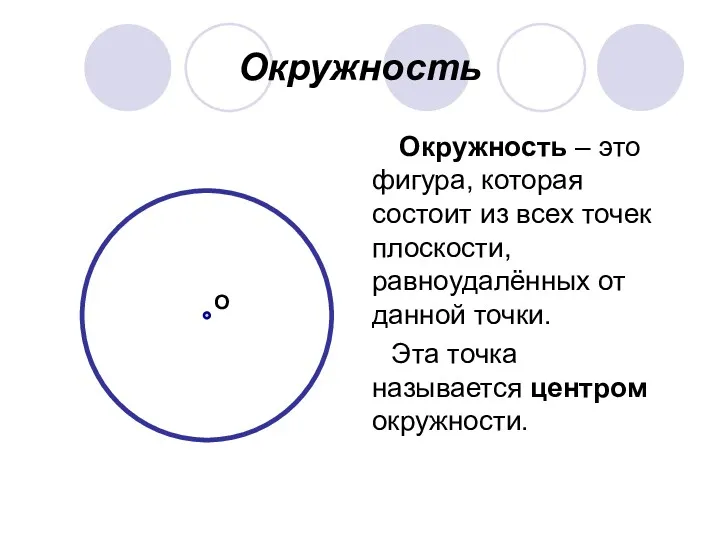 Длина окружности. Площадь круга
Длина окружности. Площадь круга Числа от 1 до 9.
Числа от 1 до 9. Использование технологий, методов и приёмов интегрированных уроков для познавательной активности на уроках математики
Использование технологий, методов и приёмов интегрированных уроков для познавательной активности на уроках математики Показательные неравенства
Показательные неравенства Скобки в числовом выражении
Скобки в числовом выражении Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Задачи на кратное сравнение
Задачи на кратное сравнение 20231011_8_klass_pryamougolnik._ploshchad_pryamougolnika
20231011_8_klass_pryamougolnik._ploshchad_pryamougolnika Геометрические фигуры
Геометрические фигуры Основы математической статистики. Лекция 3
Основы математической статистики. Лекция 3 Занимательная математика
Занимательная математика Великие математики и их открытия
Великие математики и их открытия Решение задач на нахождение площади фигур по готовым чертежам
Решение задач на нахождение площади фигур по готовым чертежам Сравнение дробей. Урок изучения нового материала в 5 классе
Сравнение дробей. Урок изучения нового материала в 5 классе Сложение рациональных чисел
Сложение рациональных чисел Родительское собрание №1. 2021-2022 учебный год
Родительское собрание №1. 2021-2022 учебный год Листая страницы истории (конференция)
Листая страницы истории (конференция) Практикум № 7 по решению стереометрических задач
Практикум № 7 по решению стереометрических задач Тела вращения. 11 класс
Тела вращения. 11 класс Цилиндр. Конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка
Цилиндр. Конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка Пропорция. Урок математики в 6 классе
Пропорция. Урок математики в 6 классе Открытый урок по математике. Тема:Задача.1 класс. Школа 2100
Открытый урок по математике. Тема:Задача.1 класс. Школа 2100 мастер класс по ФЭМП на тему: Обучению решению арифметических задач.
мастер класс по ФЭМП на тему: Обучению решению арифметических задач. Совместные действия с десятичными дробями. 6 класс
Совместные действия с десятичными дробями. 6 класс Комбинаторные методы обработки информации
Комбинаторные методы обработки информации Презентация к уроку математикиАрифметические действия над числами урок 32 программа Школа 2100
Презентация к уроку математикиАрифметические действия над числами урок 32 программа Школа 2100 Письменное умножение на двузначное число
Письменное умножение на двузначное число Метод дерева решений
Метод дерева решений