Содержание
- 3. Здесь μ = M(X) - математическое ожидание, σ2 = D(X) - дисперсия, σ = σ(X) –
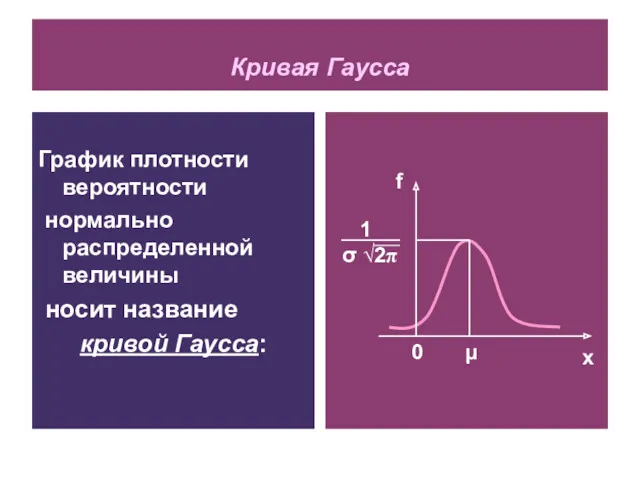
- 4. Кривая Гаусса График плотности вероятности нормально распределенной величины носит название кривой Гаусса: x f 0 μ
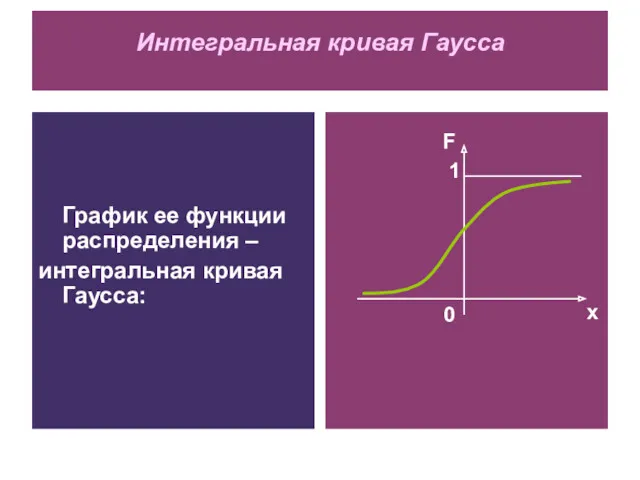
- 5. График ее функции распределения – интегральная кривая Гаусса: Интегральная кривая Гаусса F х 1 0
- 6. Введение нормированной нормальной величины Для определения вероятности попадания нормальной СВ в некоторый интервал требуется вычисление интеграла
- 7. НОРМИРОВАННАЯ НОРМАЛЬНАЯ ВЕЛИЧИНА Такая нормальная величина называется нормированной и обозначается Т. Свойства Φ (t) Φ(-∞) =
- 8. Плотность вероятности нормированной нормальной величины
- 9. Функция распределения нормированной нормальной величины
- 10. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ Φ (t) Приближенные значения Φ (t) для значений аргумента t ≥ 0 вычислены и
- 11. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ F(X) Значения функции распределения F(х) произвольной нормальной величины можно определить через нормированную путем СПЕЦИАЛЬНОЙ
- 12. Вероятность попадания значений нормальной величины в произвольный интервал Для любой нормальной величины формула имеет следующий вид:
- 13. ПРАВИЛО ТРЕХ СИГМ Вероятность того, что значения нормальной величины распределятся в окрестности ε (« эпсилон »)
- 15. ε = σ Чем больше окрестность ε, тем выше вероятность попадания в нее значений величины Х.
- 16. ε = 2σ, ε = 3σ 2) ε = 2σ. Аналогичный расчет дает вероятность 0,9544 (или
- 18. Скачать презентацию
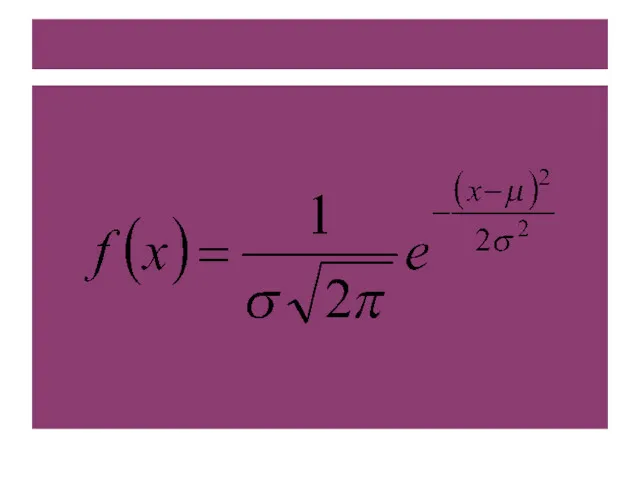









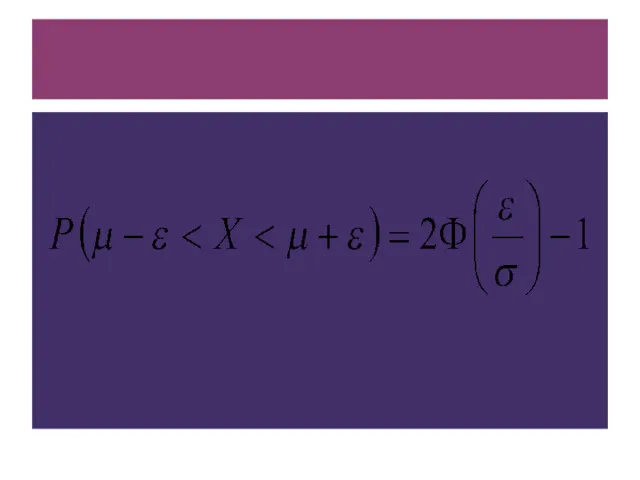


 Формулы для вычисления площадей различных треугольников
Формулы для вычисления площадей различных треугольников Численные методы расчета переходных процессов (лекция № 20)
Численные методы расчета переходных процессов (лекция № 20) математика 3 класс
математика 3 класс Обучение детей решению арифметических задач
Обучение детей решению арифметических задач Статистика и теория вероятностей. 9 класс
Статистика и теория вероятностей. 9 класс Делимость чисел. Урок-обобщение. 6 класс
Делимость чисел. Урок-обобщение. 6 класс Перпендикуляр и наклонная
Перпендикуляр и наклонная Задачи на смекалку
Задачи на смекалку Все действия с обыкновенными дробями
Все действия с обыкновенными дробями Презентация по теме Сложение. Математика, 1 класс. Программа Л.Г. Петерсон
Презентация по теме Сложение. Математика, 1 класс. Программа Л.Г. Петерсон Геометрический смысл производной. Подготовка к ЕГЭ В9
Геометрический смысл производной. Подготовка к ЕГЭ В9 Влияние коэффициентов а, b и с на расположение графика квадратичной функции. 9 класс
Влияние коэффициентов а, b и с на расположение графика квадратичной функции. 9 класс Додавання кількох чисел. Урок №55. Математика
Додавання кількох чисел. Урок №55. Математика Геометрические тела на уроках математики
Геометрические тела на уроках математики Осевая симметрия
Осевая симметрия Презентация к уроку математики с элементами экологии.
Презентация к уроку математики с элементами экологии. Математика о вреде курения
Математика о вреде курения Математическая игра для 5–6 классов. Математик-бизнесмен
Математическая игра для 5–6 классов. Математик-бизнесмен Диаграммы
Диаграммы Презентация к уроку математики по теме Действия с многозначными числами
Презентация к уроку математики по теме Действия с многозначными числами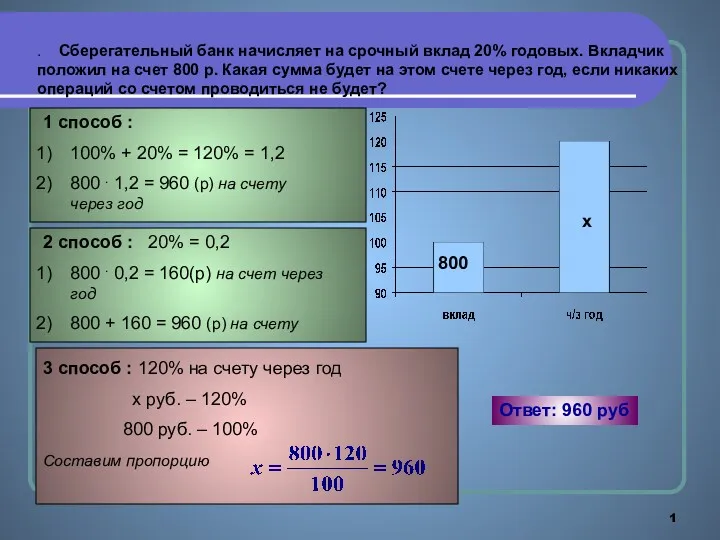 Задачи на проценты
Задачи на проценты Мастер- класс Формирование УУД на уроках математики
Мастер- класс Формирование УУД на уроках математики Системы уравнений с двумя переменными
Системы уравнений с двумя переменными Найди пару
Найди пару Математическая игра А знаешь ли ты
Математическая игра А знаешь ли ты Скалярное произведение векторов
Скалярное произведение векторов Урок математики в 1 классе по теме Знакомство с понятием Уравнение
Урок математики в 1 классе по теме Знакомство с понятием Уравнение Проектная деятельность школьников, как средство усиления прикладной направленности обучения математике
Проектная деятельность школьников, как средство усиления прикладной направленности обучения математике