Содержание
- 2. каф. ТОЭ МЭИ 2016 Численные методы расчета переходных процессов Лекция № 20 Состояние цепи после коммутации
- 3. каф. ТОЭ МЭИ 2016 Численные методы расчета переходных процессов Лекция № 20 Численное решение на интервале
- 4. каф. ТОЭ МЭИ 2016 Методы численного интегрирования Лекция № 20 разностное уравнение
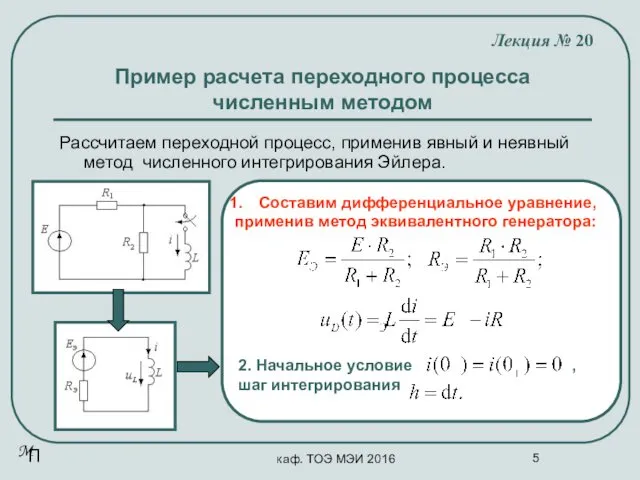
- 5. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса численным методом Лекция № 20 Рассчитаем переходной процесс,
- 6. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса численным методом Лекция № 20 Рассчитаем переходной процесс,
- 7. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса численным методом Лекция № 20 Результаты численного интегрирования
- 8. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса численным методом Лекция № 20 Результаты численного интегрирования
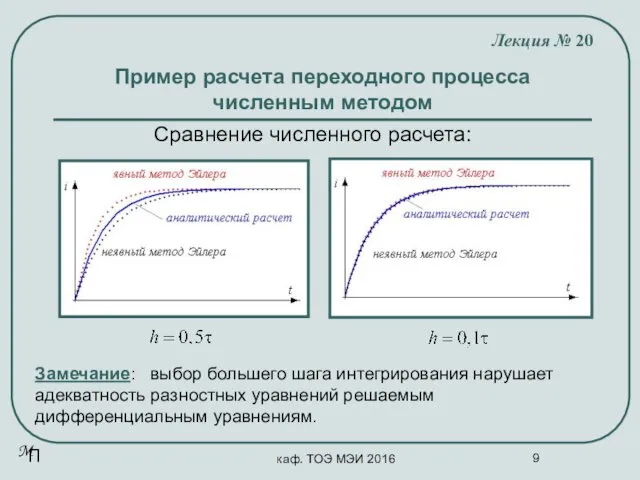
- 9. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса численным методом Лекция № 20 Сравнение численного расчета:
- 10. каф. ТОЭ МЭИ 2016 Метод дискретных схем замещения Лекция № 20 При замене дифференциальных уравнений конечно-разностными
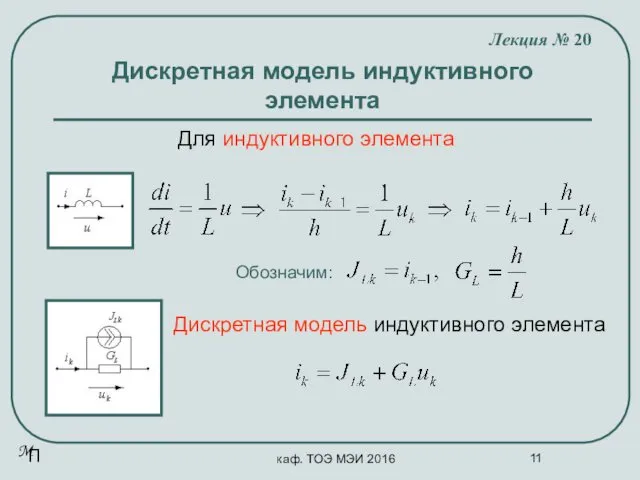
- 11. каф. ТОЭ МЭИ 2016 Дискретная модель индуктивного элемента Лекция № 20 Для индуктивного элемента Обозначим: Дискретная
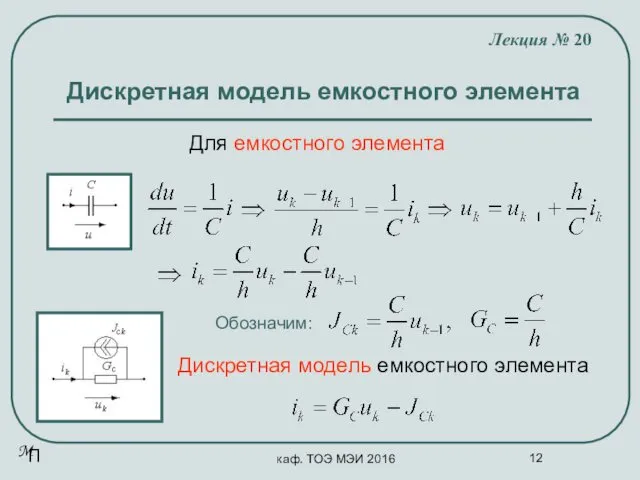
- 12. каф. ТОЭ МЭИ 2016 Дискретная модель емкостного элемента Лекция № 20 Для емкостного элемента Обозначим: Дискретная
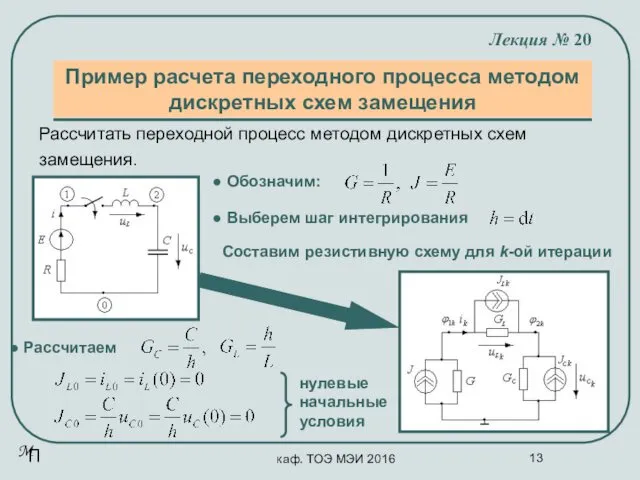
- 13. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса методом дискретных схем замещения Лекция № 20 Рассчитать
- 14. каф. ТОЭ МЭИ 2016 Пример расчета переходного процесса методом дискретных схем замещения Лекция № 20 Методом
- 15. каф. ТОЭ МЭИ 2016 Замечания Лекция № 20 Подобные резистивные схемы синтезируют топологические особенности электрических цепей
- 16. каф. ТОЭ МЭИ 2016 «Жёсткие» и «дребезжащие» модели электрических цепей Лекция № 20 При составлении математических
- 17. каф. ТОЭ МЭИ 2016 Пример, иллюстрирующий явление «жесткости» Лекция № 20 При моделировании процесса разрядки конденсатора
- 18. каф. ТОЭ МЭИ 2016 «Жёсткие» системы, уравнения и модели электрических цепей Лекция № 20 Жесткими называют
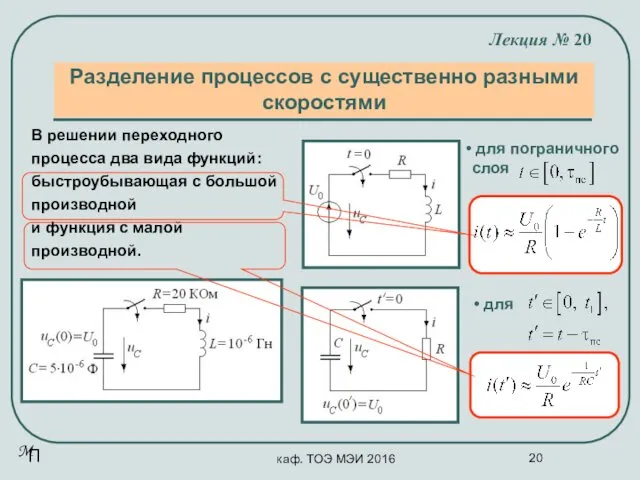
- 19. каф. ТОЭ МЭИ 2016 Пример, иллюстрирующий явление «жесткости» Лекция № 20 В решении переходного процесса два
- 20. каф. ТОЭ МЭИ 2016 для пограничного слоя Разделение процессов с существенно разными скоростями Лекция № 20
- 21. каф. ТОЭ МЭИ 2016 Замечания Лекция № 20 Если проблема жесткости аналитически решается разделением процессов с
- 23. Скачать презентацию














 Умножение 7 и на 7
Умножение 7 и на 7 Системы ходов. Виды теодолитных ходов
Системы ходов. Виды теодолитных ходов Урок математики в 3 классе
Урок математики в 3 классе Система обобщающего повторения на уроках геометрии при подготовке к ГИА
Система обобщающего повторения на уроках геометрии при подготовке к ГИА Математические модели в экономике
Математические модели в экономике Именованные числа. Тренажёр
Именованные числа. Тренажёр Применение производной к решению экономических задач
Применение производной к решению экономических задач Вероятность события
Вероятность события Чтение многозначных чисел
Чтение многозначных чисел Признаки делимости на 3 и 9
Признаки делимости на 3 и 9 Тест. Прямоугольный треугольник
Тест. Прямоугольный треугольник Система старинных русских мер
Система старинных русских мер Интегрированное занятие по ФЭМП в средней группе
Интегрированное занятие по ФЭМП в средней группе Инвариантность систем
Инвариантность систем Сравнение десятичных дробей
Сравнение десятичных дробей Нахождение площади и периметра
Нахождение площади и периметра Теорема Фалеса 1
Теорема Фалеса 1 Алгебра логики. Контрольная работа
Алгебра логики. Контрольная работа Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Секреты умножения и деления
Секреты умножения и деления Производная в биологии и химии
Производная в биологии и химии Основыне понятия теории погрешностей
Основыне понятия теории погрешностей Запись и чтение чисел второго десятка
Запись и чтение чисел второго десятка Решение задач на движение
Решение задач на движение Предел функции на бесконечности
Предел функции на бесконечности Определитель. Линейная алгебра
Определитель. Линейная алгебра Составляем и решаем задачи
Составляем и решаем задачи По страницам учебника математики (8 класс)
По страницам учебника математики (8 класс)