Содержание
- 2. Непрерывное распределение, которое занимает наиболее важное положение в теории и практике статистики − распределение Гаусса, или
- 3. 3) Является пределом для других ЗР при некотором n → ∞ (биномиальный при ∞ числе испытаний)
- 4. Ошибки измерений часто нормальны (такие распределения обнаружили астрономы в 18 веке) В статистике − распределение выборочного
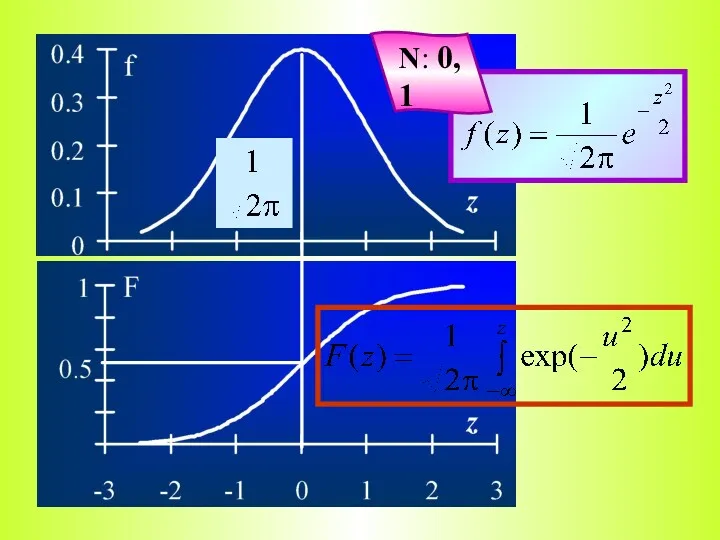
- 5. СВ распределена по нормальному закону если ее функция плотности равна Тогда
- 6. Функция распределения нормальной величины определяется как Параметры μ и σ2 − матожидание и дисперсия Это двухпараметрический
- 7. N: μ, σ Чем это распределение отличается от следующего? NB!
- 8. N: 0, 1
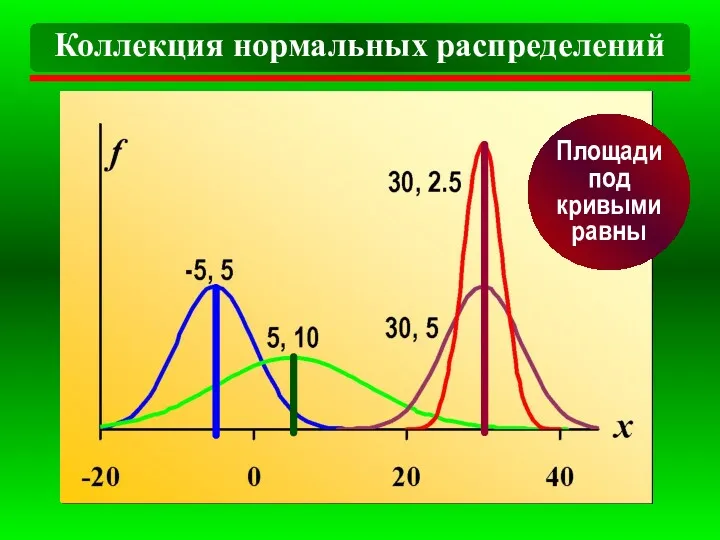
- 9. Коллекция нормальных распределений Площади под кривыми равны
- 10. Различия: ∙ привязаны к разным точкам μ числовой оси ∙ чем площадь под кривой вблизи μ,
- 11. Стандартный нормальный закон Будучи стандартом для других ЗР, нормальное распределение имеет свой собственный стандарт Это N:
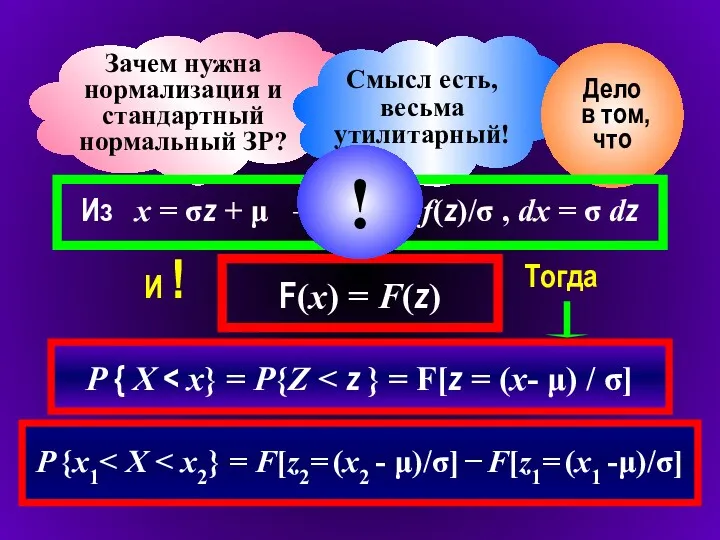
- 12. Зачем нужна нормализация и стандартный нормальный ЗР? Смысл есть, весьма утилитарный! Дело в том, что Из
- 13. Вместо расчета интегралов всякий раз для разных μ и σ, можно использовать раз и навсегда рассчитанные
- 14. У нее следующие свойства: Φ(0) = 0; Φ(∞) = 0.5; это нечетная функция, Φ(− z) =
- 15. Удобное практическое правило Вероятность того, что нормальная величина примет значение из некоторого интервала равна разности значений
- 16. P{150 Φ[z2 = (200-160)/20=2] − Φ[z1 =(150-160)/20=-0.5] = Φ(2) + Φ(0.5) = 0.4472 + 0.1915 =
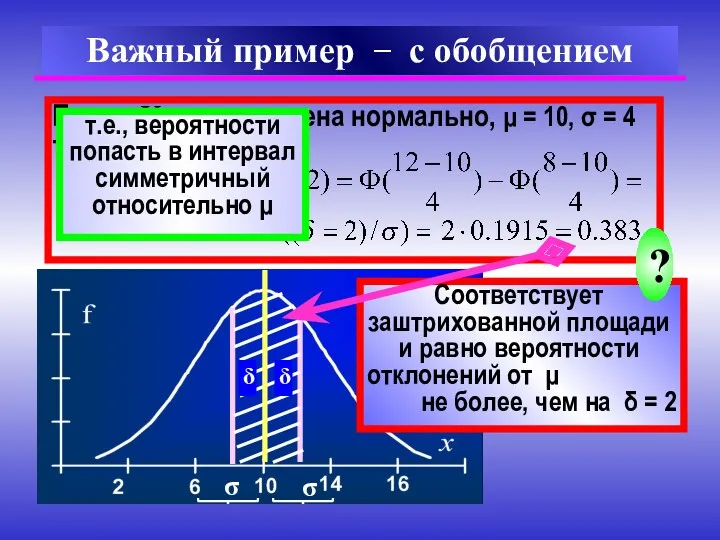
- 17. Пусть X распределена нормально, μ = 10, σ = 4 Тогда Важный пример − с обобщением
- 18. Общее правило Вероятность того, что (при измерении, управлении, производстве …) отклонение от μ (неизвестного истинного, предписанного
- 19. Очевидно! риск выйти за нормативные границы шансы отклонений, превышающих заданное δ определяет !!! !
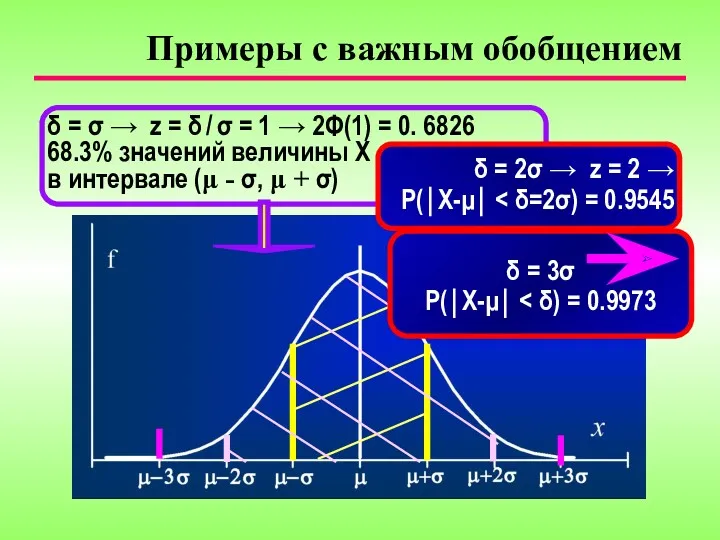
- 20. Примеры с важным обобщением δ = σ → z = δ / σ = 1 →
- 21. 99.7% значений нормально распределенной величины попадают в интервал (μ ± 3σ) Тогда P(⏐X−μ⏐ > 3σ) =
- 23. Скачать презентацию











![P{150 Φ[z2 = (200-160)/20=2] − Φ[z1 =(150-160)/20=-0.5] = Φ(2) +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/272531/slide-15.jpg)



 Параллельные прямые. (7 класс)
Параллельные прямые. (7 класс) Тренажёр по математике Морское приключение. Счёт в пределах 10
Тренажёр по математике Морское приключение. Счёт в пределах 10 Магические квадраты. История появления магических квадратов
Магические квадраты. История появления магических квадратов счёт
счёт Делимое, делитель, частное
Делимое, делитель, частное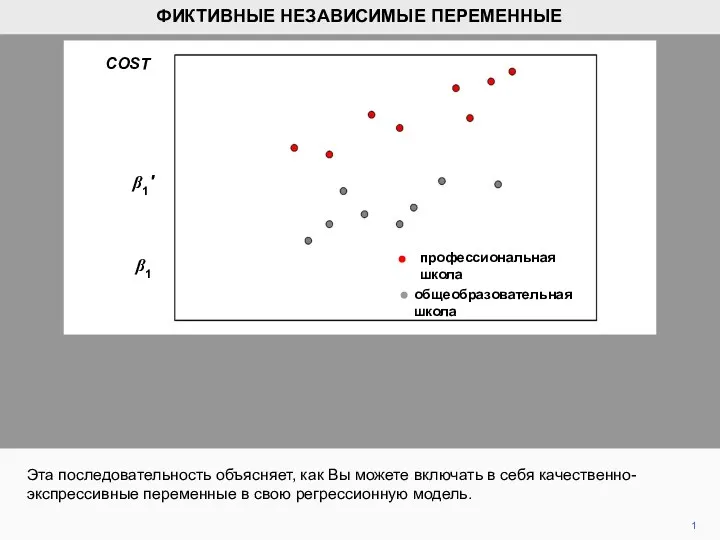 Фиктивные независимые переменные
Фиктивные независимые переменные Правильные многоугольники. 8 класс
Правильные многоугольники. 8 класс Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник
Описанная окружность. Треугольник, вписанный в окружность. Касательная к окружности. Окружность, вписанная в треугольник Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач Симметрия в кубе, параллелепипеде, в призме, в пирамиде
Симметрия в кубе, параллелепипеде, в призме, в пирамиде Прямоугольник и квадрат. Площадь фигур
Прямоугольник и квадрат. Площадь фигур Криптографическая защита информации. Элементы теории чисел. (Лекция 3)
Криптографическая защита информации. Элементы теории чисел. (Лекция 3) Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ
Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ Своя игра. Математический турнир
Своя игра. Математический турнир Конкурс педагогического мастерства От теории к практике - Решение задач
Конкурс педагогического мастерства От теории к практике - Решение задач Площадь трапеции
Площадь трапеции 8_klassё
8_klassё Основні види моделювання. Формальні методи побудови моделей
Основні види моделювання. Формальні методи побудови моделей Сокращение дробей. Упражнение 6
Сокращение дробей. Упражнение 6 Свойства прямоугольных треугольников
Свойства прямоугольных треугольников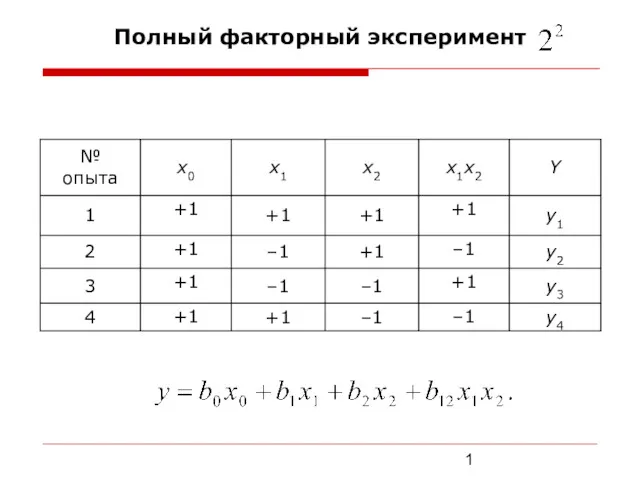 Полный факторный эксперимент
Полный факторный эксперимент Развёртки поверхностей. Аксонометрические проекции
Развёртки поверхностей. Аксонометрические проекции Переход от одних единиц измерения к другим
Переход от одних единиц измерения к другим Компланарные векторы
Компланарные векторы Внеклассное занятие по математике .Гимнастика для ума
Внеклассное занятие по математике .Гимнастика для ума Учтный счет, 1 класс
Учтный счет, 1 класс Начертательная геометрия. Пересечение линии и поверхности
Начертательная геометрия. Пересечение линии и поверхности Презентация к открытому уроку по математике Числа от 1 до 10
Презентация к открытому уроку по математике Числа от 1 до 10