Содержание
- 2. Квадратная матрица A-1 порядка n называется обратной матрицей для данной матрицы A, если A·A-1=A-1·A=E(единичная матрица) Если
- 3. Найти матрицу A-1, если => матрица A невырожденная и имеет обратную матрицу A-1.
- 4. A·X=B A-1·(A·X)=A-1·B (A-1·A)·X=A-1·B E·X=A-1·B X=A-1·B Матричный способ решения линейной системы уравнений.
- 5. Матричный способ решения линейной системы уравнений.
- 6. Решить матричным способом систему уравнений
- 7. Формулы Крамера. … …
- 8. Решить по формулам Крамера систему уравнений
- 9. Ранг матрицы. Теорема Кронекера-Капелли. Метод Гаусса.
- 10. Квадратная матрица A-1 порядка n – обратная матрица для данной матрицы A, если A-1 = A-1
- 11. Выделить в матрице k строк и k столбцов (k≤min(m,n)) Из элементов, стоящих на пересечении выделенных строк
- 12. Свойства ранга матрицы При транспонировании матрицы её ранг не меняется Если вычеркнуть из матрицы нулевой ряд,
- 13. Система, имеющая хотя бы одно решение, называется совместной. Система, имеющая только одно решение, называется определённой. Система,
- 15. Теорема Кронекера-Капели: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы
- 16. Правило решения произвольной системы линейных уравнений. Найти ранг основной и расширенной матриц системы. Если r(Ã)≠r(A), то
- 17. Исключим с помощью первого уравнения неизвестную x1 из остальных уравнений: Получим: Аналогично исключим с помощью второго
- 18. И тогда: xn=bnn . Подставляя это значение в предпоследнее уравнение системы найти xn-1. Подставляя найденные значения
- 21. Скачать презентацию


















 Математика повсюду
Математика повсюду Гетероскедастичность и ее последствия
Гетероскедастичность и ее последствия Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Анализ показателей динамического ряда
Анализ показателей динамического ряда Полярные координаты. Параметрическая форма кривых
Полярные координаты. Параметрическая форма кривых Теорема Виета 1
Теорема Виета 1 Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Проектная деятельность как средство развития абстрактного мышления обучающихся
Проектная деятельность как средство развития абстрактного мышления обучающихся Сложение числа 5 с однозначными числами
Сложение числа 5 с однозначными числами Площадь. Многоугольник
Площадь. Многоугольник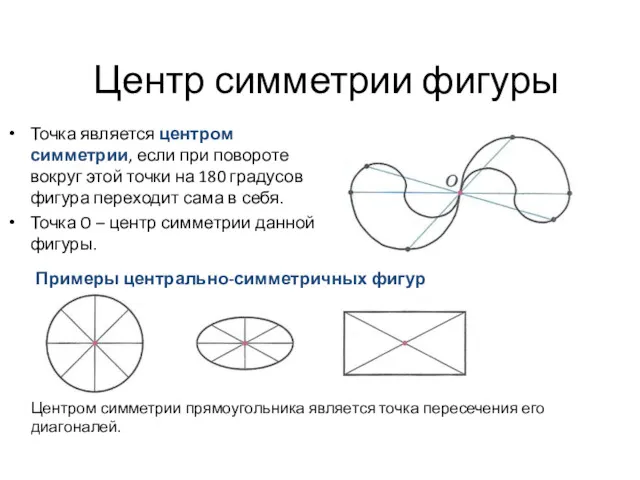 Центр симметрии фигуры
Центр симметрии фигуры Точки перегиба функции, выпуклость графика функции
Точки перегиба функции, выпуклость графика функции Тела вращения. 11 класс
Тела вращения. 11 класс Презентация по ПДД
Презентация по ПДД Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера)
Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера) Измерения, погрешности и точности
Измерения, погрешности и точности Свойства числовых неравенств
Свойства числовых неравенств Project Poisson process
Project Poisson process Движение. Виды движения. Симметрия
Движение. Виды движения. Симметрия Сравнение дробей. Дроби с одинаковыми знаменателями
Сравнение дробей. Дроби с одинаковыми знаменателями Решение уравнений из материалов ЕГЭ по математике
Решение уравнений из материалов ЕГЭ по математике Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28
Доба. Замкнені і незамкнені лінії. Повторення вивченого. Урок №28 Готовимся к ЕГЭ. Математика
Готовимся к ЕГЭ. Математика Простой процентный рост. Сложный процентный рост
Простой процентный рост. Сложный процентный рост Математическая разминка для 1 класса
Математическая разминка для 1 класса Треугольники. Подготовка к ОГЭ. Задание 16
Треугольники. Подготовка к ОГЭ. Задание 16 График функции
График функции