Содержание
- 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид: Решение этих уравнений основано на
- 3. Рассмотрим способ нахождения частного решения неоднородного уравнения, ограничиваясь решением таких неоднородных уравнений второго порядка, у которых
- 4. а) если Р(х) – многочлен и q≠0, то у* следует искать в виде многочлена такой же
- 5. # у" - 2у' - 3у = 2х нач. усл.: у(0) = 0 у'(0) = 1
- 6. k2 — 2k — 3 = 0 D = 4 + 12 = 16 k2 =
- 8. б) q = 0 (при этом характеристическое уравнение имеет один нулевой корень), то в многочлене, для
- 9. в) если р = 0 и q = 0, то в многочлен у* вводятся множитель х2.
- 10. II. Подбор частного решения у* когда правая часть – показательная функция. а) если в правой части
- 11. в) если правая часть – сумма функций различного вида, то частное решение составляется в виде суммы
- 12. # y" – 3y' – 4y = 9e2x k2 – 3k – 4 = 0 D
- 14. Скачать презентацию



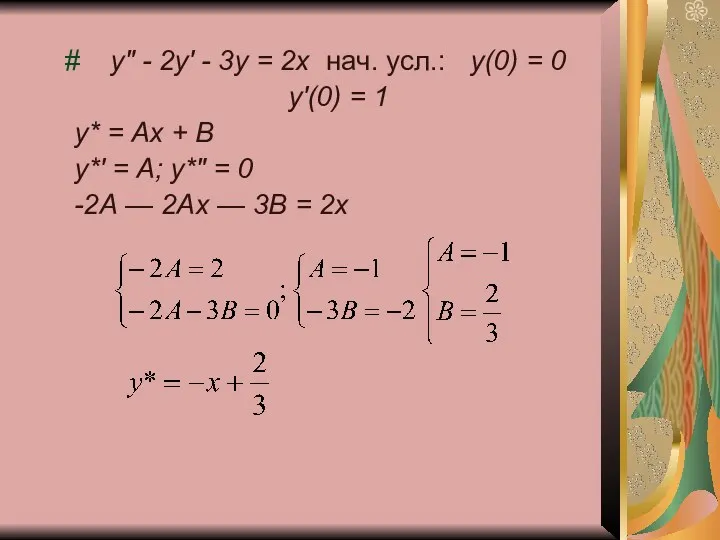
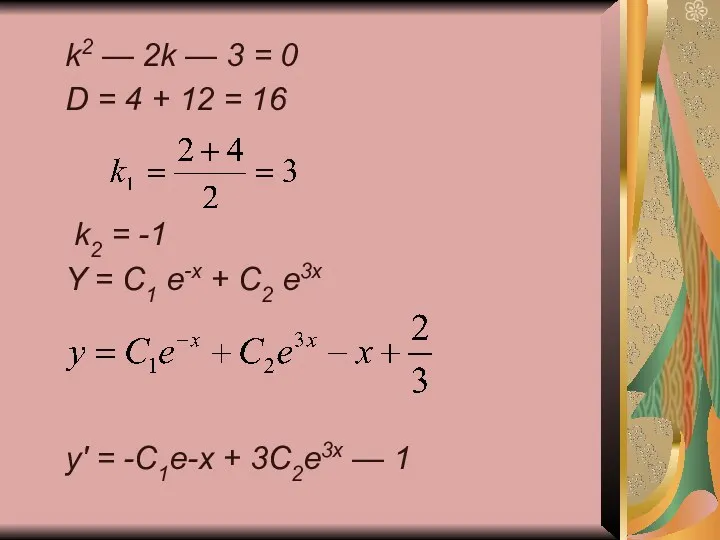




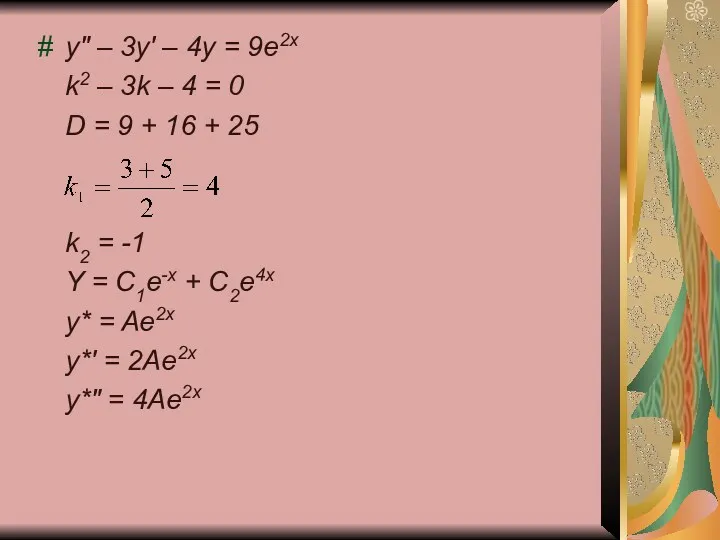
 Задачі на збільшення на декілька одиниць. Порівняння виразу і числа. Урок №54. Математика
Задачі на збільшення на декілька одиниць. Порівняння виразу і числа. Урок №54. Математика Синквейн на уроках математики и не только… мастер-класс по составлению и применению
Синквейн на уроках математики и не только… мастер-класс по составлению и применению Моделирование алгоритмов вейвлет-преобразования. Гармоническое вейвлетпреобразование
Моделирование алгоритмов вейвлет-преобразования. Гармоническое вейвлетпреобразование Отношения и проценты
Отношения и проценты Тригонометрия. Тригонометрические функции и их графики
Тригонометрия. Тригонометрические функции и их графики Координаты на плоскости. 6 класс
Координаты на плоскости. 6 класс Построение графика квадратичной функции
Построение графика квадратичной функции Применение кейс технологий на уроках математики
Применение кейс технологий на уроках математики Треугольники. Признаки равенства треугольников
Треугольники. Признаки равенства треугольников Личностно ориентированные технологии на уроках математики
Личностно ориентированные технологии на уроках математики Урок 15. Точечная оценка числовой характеристики случайной величины, ее свойства
Урок 15. Точечная оценка числовой характеристики случайной величины, ее свойства Двойной интеграл: определение, свойства, вычисление в ПДСК
Двойной интеграл: определение, свойства, вычисление в ПДСК Конспект урока по математике в 3 классепо теме Уравнение. Обобщение и закрепление знаний
Конспект урока по математике в 3 классепо теме Уравнение. Обобщение и закрепление знаний Вычитания с переходом через десяток
Вычитания с переходом через десяток Решение показательных уравнений. 10 класс
Решение показательных уравнений. 10 класс Алгоритм Евклида. Линейные диофантовы уравнения с двумя неизвестными
Алгоритм Евклида. Линейные диофантовы уравнения с двумя неизвестными Теорія відношень
Теорія відношень Алгоритмы и способы описания алгоритмов
Алгоритмы и способы описания алгоритмов Метод координат на плоскости
Метод координат на плоскости Координатная плоскость
Координатная плоскость Нахождение части от целого
Нахождение части от целого Метрология. Объекты метрологии
Метрология. Объекты метрологии Решение тригонометрических уравнений. (10 класс)
Решение тригонометрических уравнений. (10 класс) Три проекции призмы. (Задача 62)
Три проекции призмы. (Задача 62) Викторина по математике для 6 класса (итоги года)
Викторина по математике для 6 класса (итоги года) Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Разложение на простые множители ( 6 класс )
Разложение на простые множители ( 6 класс ) Симметрия
Симметрия