Содержание
- 2. Здесь мы вспомним тригонометрические уравнения специального вида, довольно часто встречающиеся на практике.
- 3. Определение Уравнения вида asinx+bcosx=0 называют однородным тригонометрическим уравнением первой степени Уравнения вида asin2x+bsinxcosx+ccos2x=0 называют однородным тригонометрическим
- 4. Сначала поговорим о решении однородных тригонометрических уравнений первой степени, причем рассмотрим только самый общий случай, когда
- 5. Итак, дано уравнение asinx+bcosx=0, где a≠0, b≠0. Разделив обе части уравнения почленно на cosx, получим: asinx/cosx
- 6. Но внимание! Вообще-то, делить обе части уравнения на одно и то же выражение можно только в
- 7. Уравнение вида asinmx+bcosmx=0 тоже называют однородным тригонометрическим уравнением первой степени. Для их решения обе части уравнения
- 8. Примеры №1. Решить уравнение 2sinx-3cosx=0 Решение. Разделив обе части уравнения почленно на cosx, получим 2tgx-3=0 tgx=3/2
- 9. №2. Решить уравнение sin2x+cos2x=0 Решение. Разделив обе части уравнения почленно на cos2x, получим tg2x+1=0, tg2x=-1 2x=-π/4+
- 10. Рассмотрим теперь однородное тригонометрическое уравнение второй степени asin2x+bsinxcosx+ccos2x=0. Если коэффициент а отличен от нуля, то есть
- 11. Пусть теперь в однородном тригонометрическом уравнении asin2x+bsinxcosx+ccos2x=0 коэффициент а=0, то есть отсутствует член asin2x. Тогда уравнение
- 12. Алгоритм решения однородных тригонометрических уравнений второй степени Посмотреть, есть ли в уравнении член asin2x; Если этот
- 13. Так же обстоит дело и в однородном тригонометрическом уравнении второй степени вида asin2mx+bsinmxcosmx+ccos2mx=0
- 14. Примеры №1. Решить уравнение sin2x-3sinxcosx+2cos2x=0. Решение. sin2x-3sinxcosx+2cos2x=0 \ ÷ cos2x tg2x-3tgx+2=0 Введем новую переменную z=tgx z2-3z+2=0
- 16. Скачать презентацию













 Квадратичная функция и её свойства
Квадратичная функция и её свойства Визначники матриць (продовження). Системи лінійних рівнянь
Визначники матриць (продовження). Системи лінійних рівнянь Решение заданий
Решение заданий Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов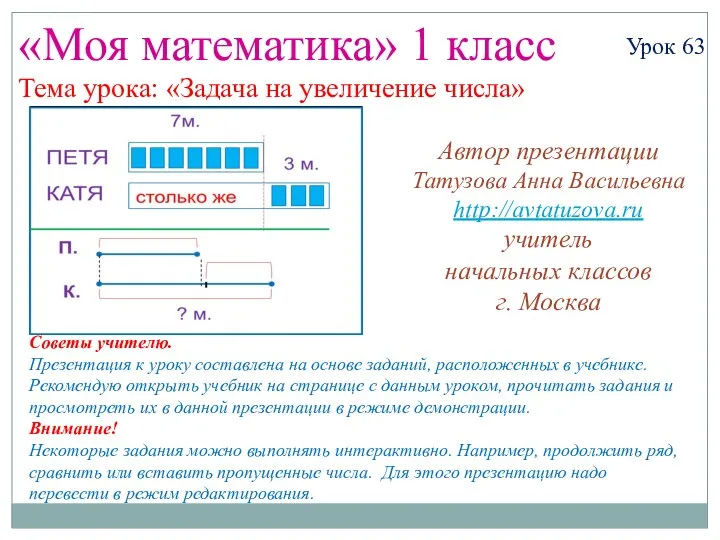 Математика. 1 класс. Урок 63. Задача на увеличение числа - Презентация
Математика. 1 класс. Урок 63. Задача на увеличение числа - Презентация Конспект урока по теме: Сфера. Уравнение сферы
Конспект урока по теме: Сфера. Уравнение сферы Формирование регулятивных универсальных учебных действий на уроках математики в начальной школе
Формирование регулятивных универсальных учебных действий на уроках математики в начальной школе Введение в биостатистику
Введение в биостатистику Игра Молчанка Диск
Игра Молчанка Диск Метод решения систем линейных уравнений методом Крамера. Лекция №10
Метод решения систем линейных уравнений методом Крамера. Лекция №10 Преобразования пространства
Преобразования пространства Расстояние между точками координатной прямой
Расстояние между точками координатной прямой Уравнение. 5 класс
Уравнение. 5 класс Действия с рациональными числами
Действия с рациональными числами Открытый урок по теме Единицы массы
Открытый урок по теме Единицы массы Производная показательной функции. Число е.11 класс
Производная показательной функции. Число е.11 класс Тест по математике за курс начальной школы
Тест по математике за курс начальной школы Призма. Определение, элементы, виды
Призма. Определение, элементы, виды Математический КВН для 3 класса
Математический КВН для 3 класса Обобщающий урок по теме Вписанные и описанные многоугольники
Обобщающий урок по теме Вписанные и описанные многоугольники Формулы косинуса суммы и разности двух аргументов
Формулы косинуса суммы и разности двух аргументов Задачи на смекалку
Задачи на смекалку Круглые тела
Круглые тела Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел Вписанный угол
Вписанный угол занятие 105.Первообразная.Неопределенный интеграл
занятие 105.Первообразная.Неопределенный интеграл Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Занимательная математика
Занимательная математика