Содержание
- 2. 1. 2. 3. , k-любое число
- 3. 4. 5.Аддитивность определённого интеграла. Для любых чисел a,b,c справедливо:
- 4. 6) Если на , то 7) Если на
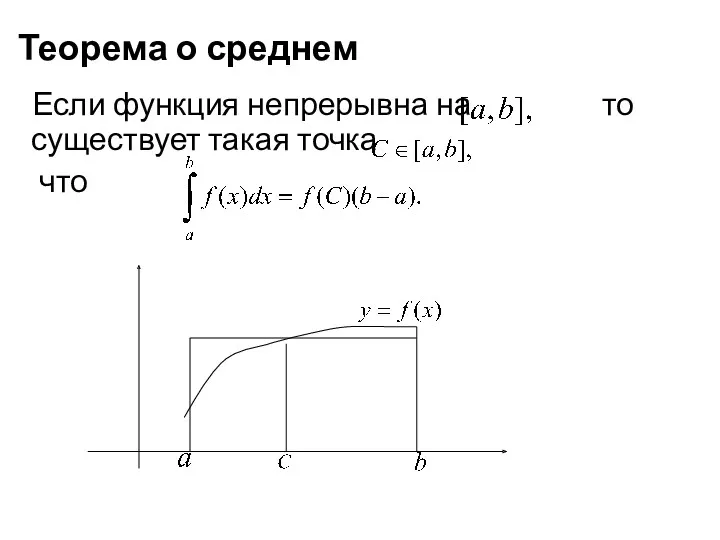
- 5. Теорема о среднем Если функция непрерывна на то существует такая точка что
- 6. Формула Ньютона-Лейбница. Если F(x) есть какая-либо первообразная от непрерывной на [ , ] функции f(x), то
- 7. Пример.
- 8. Методы интегрирования
- 10. Интегрирование по частям в определённом интеграле.
- 12. Геометрические приложения определенного интеграла
- 13. 1. Если непрерывна и положительна, то с основанием ограниченной сверху графиком этой функции можно найти по
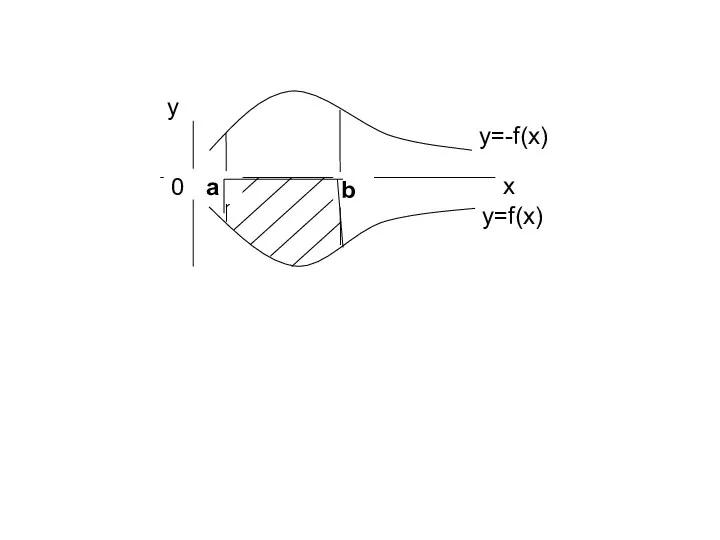
- 14. 2. Если на .
- 15. a
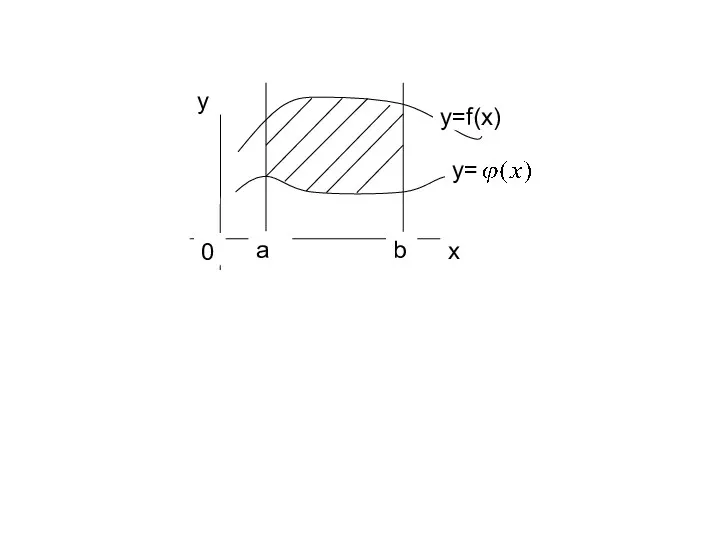
- 16. 3.Рассмотрим случай, когда фигура ограничена сверху графиком функции , снизу графиком функции
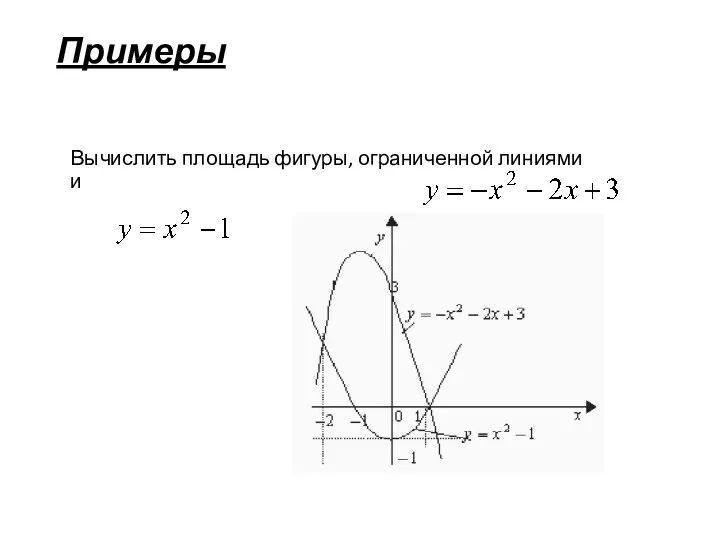
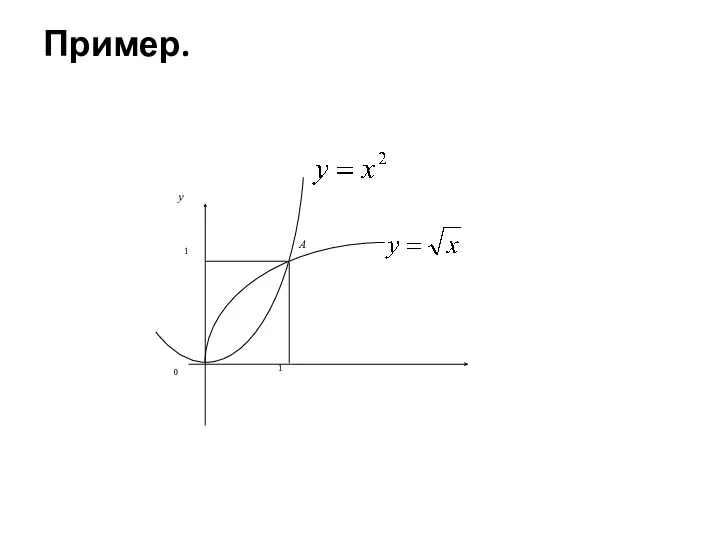
- 19. Примеры Вычислить площадь фигуры, ограниченной линиями и
- 20. Получим
- 21. Вычисление площадей В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой
- 22. Пример. Найти площадь эллипса . Параметрические уравнения эллипса у о х
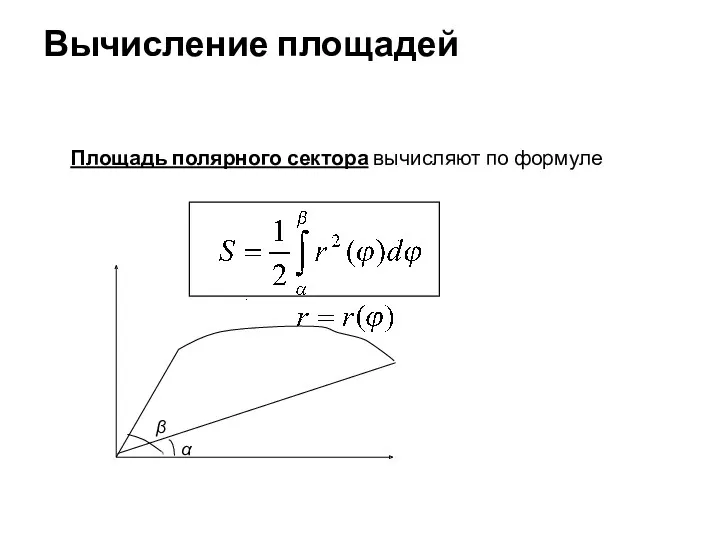
- 23. Вычисление площадей Площадь полярного сектора вычисляют по формуле . α β
- 24. Пример. Площадь фигуры, ограниченной лемнискатой Бернулли и лежащей вне круга радиуса :
- 25. Вычисление длины дуги Если кривая задана параметрическими уравнениями , , то длина ее дуги где –значения
- 26. Длина дуги в декартовых координатах Если кривая задана уравнением , то где a, b–абсциссы начала и
- 27. Длина дуги в полярных координатах Если кривая задана уравнением в полярных координатах , то где –значения
- 28. Пример. Вычислить длину дуги кривой от точки до . , тогда
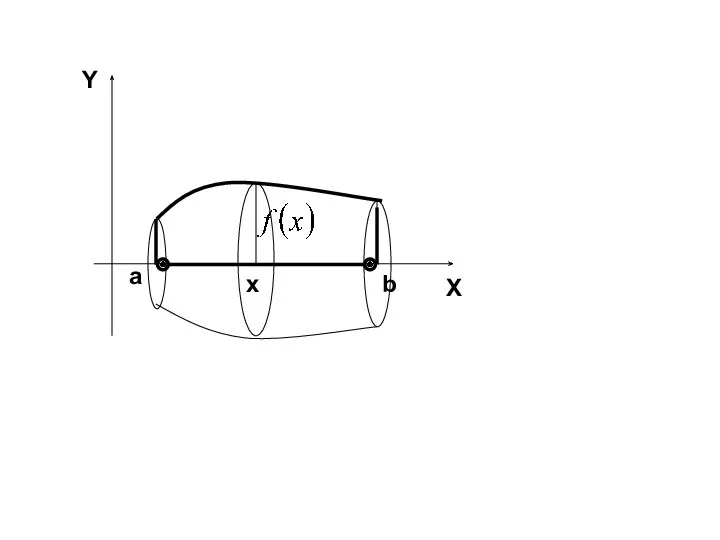
- 29. Вычисление объема тела вращения. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой ,
- 30. X Y b a x
- 31. Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком
- 32. Пример.
- 33. Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных линиями
- 35. Скачать презентацию
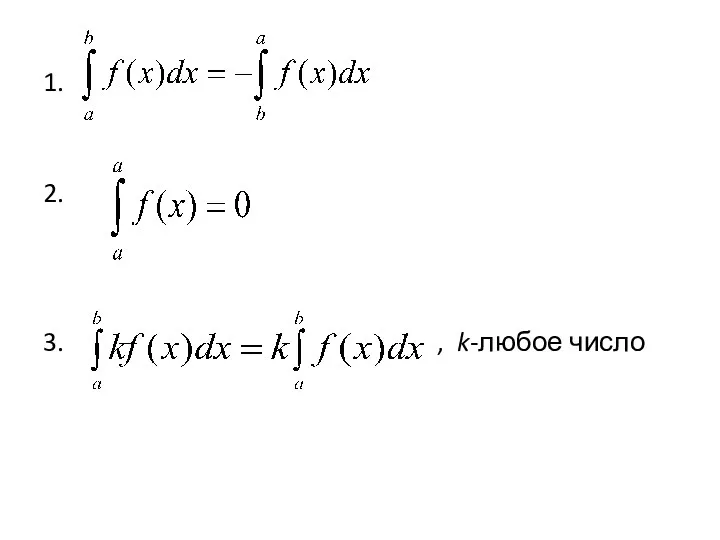
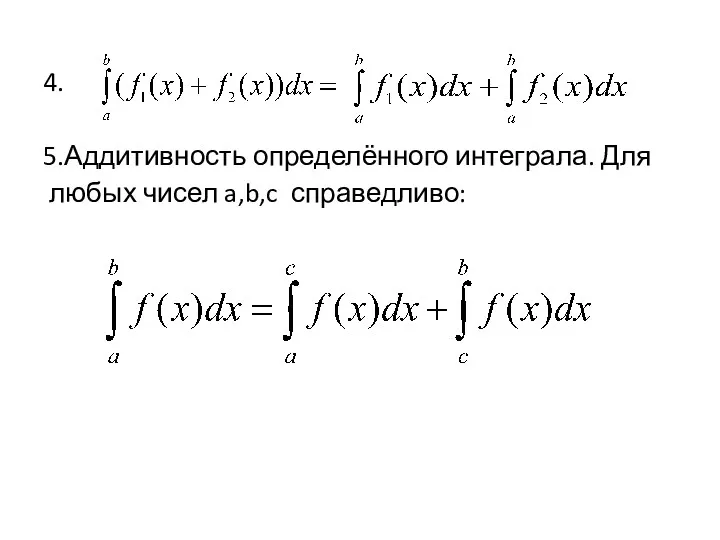
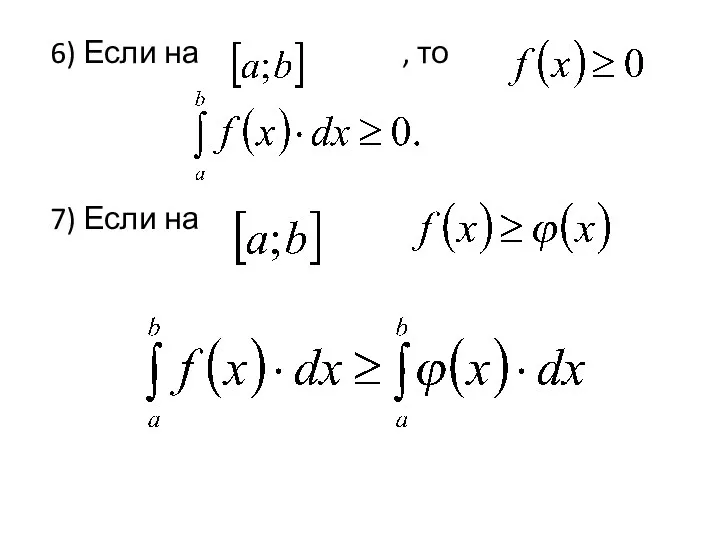



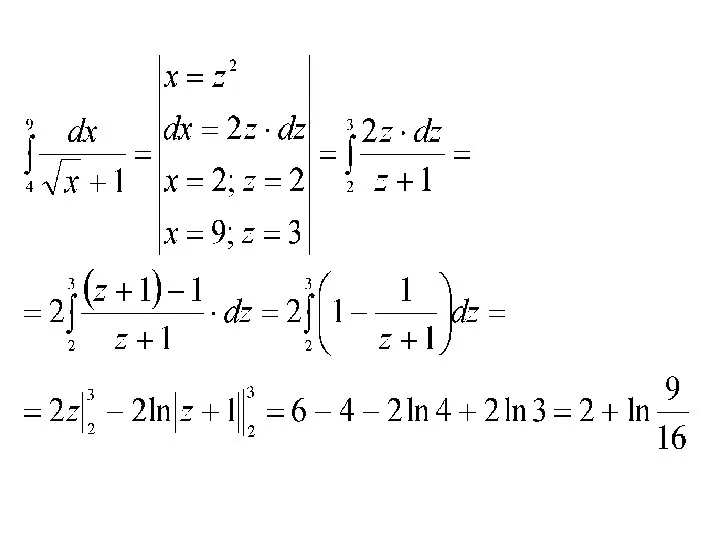

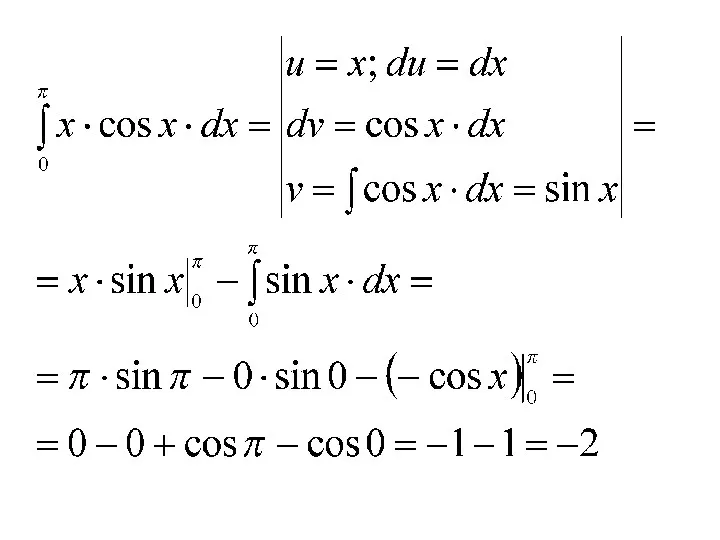


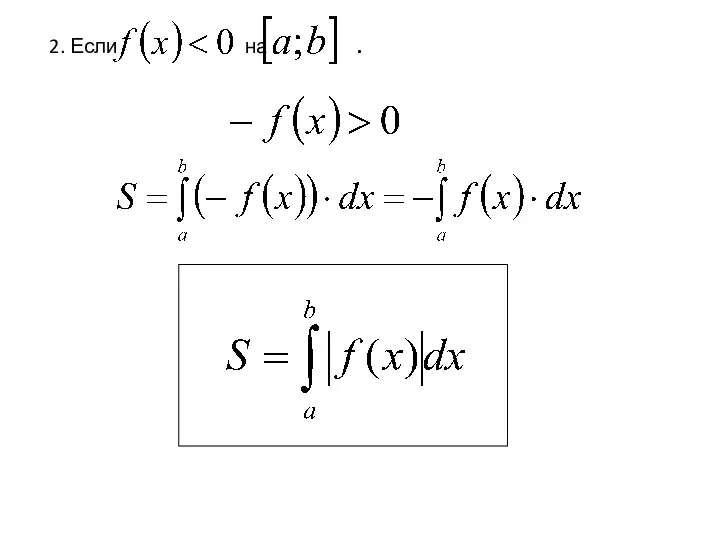

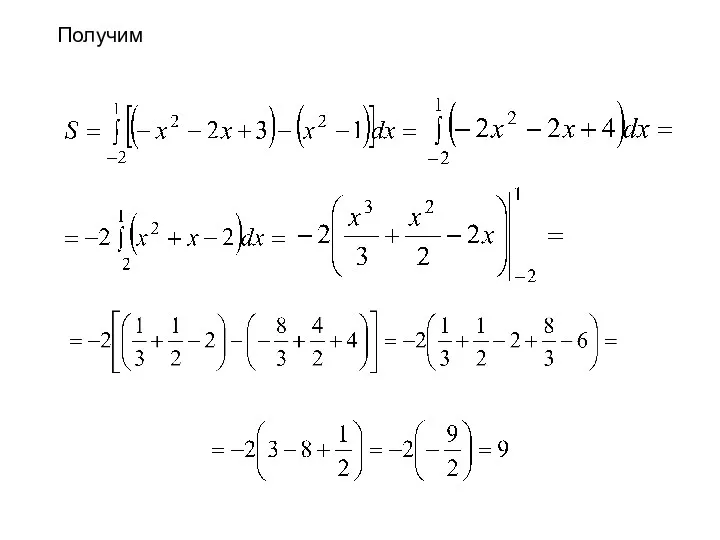










 Подобные слагаемые
Подобные слагаемые Координатная плоскость
Координатная плоскость Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Интеграл и его практическое применение
Интеграл и его практическое применение Задачи на увеличение (уменьшение) числа на несколько единиц.
Задачи на увеличение (уменьшение) числа на несколько единиц. Касательная. Уравнение касательной
Касательная. Уравнение касательной Сложение и вычитание чисел в пределах 10. Игра-тренажёр
Сложение и вычитание чисел в пределах 10. Игра-тренажёр Площадь прямоугольника, объём параллелепипеда , формулы…
Площадь прямоугольника, объём параллелепипеда , формулы… ПРЕЗЕНТАЦИЯ ОБЪЕМ
ПРЕЗЕНТАЦИЯ ОБЪЕМ Теорема Пифагора
Теорема Пифагора Компьютерный практикум по алгебре в среде Matlab
Компьютерный практикум по алгебре в среде Matlab Интерактивный тренажер Нахождение производной функции
Интерактивный тренажер Нахождение производной функции Решето Эратосфена
Решето Эратосфена Урок математики в 3 классе Масленица. Решение задач
Урок математики в 3 классе Масленица. Решение задач Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Система подготовки учащихся к ОГЭ по математике
Система подготовки учащихся к ОГЭ по математике Математика о вреде курения
Математика о вреде курения Некоторые другие приемы сравнения дробей
Некоторые другие приемы сравнения дробей Осевая и центральная симметрия, 8 класс
Осевая и центральная симметрия, 8 класс Решение задач с помощью уравнений
Решение задач с помощью уравнений Системы уравнений. Система двух линейных уравнений с двумя неизвестными
Системы уравнений. Система двух линейных уравнений с двумя неизвестными Решение неравенств методом интервалов. 9 класс
Решение неравенств методом интервалов. 9 класс Study quadrilateral concepts of its elements. Quadrilaterals. lesson 1
Study quadrilateral concepts of its elements. Quadrilaterals. lesson 1 Незнайкины задачки (1 класс)
Незнайкины задачки (1 класс) Учимся выполнять умножение. урок 37. 1 класс. УМК Начальная школа 21 века
Учимся выполнять умножение. урок 37. 1 класс. УМК Начальная школа 21 века Умножение десятичных дробей на натуральные числа. 5 класс
Умножение десятичных дробей на натуральные числа. 5 класс Умножение рациональных чисел
Умножение рациональных чисел урок математики
урок математики