Цель занятия:
Ввести понятие определённого интеграла и его вычисление по формуле Ньютона-Лейбница,
используя знания о первообразной и правила её вычисления
Задачи занятия:
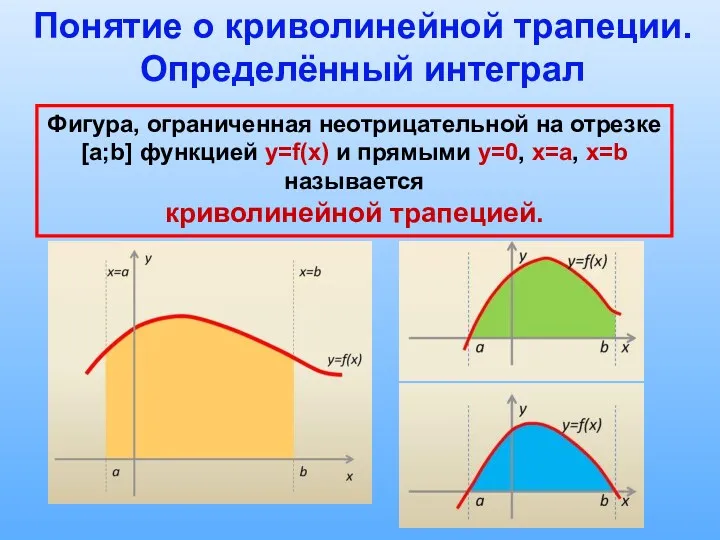
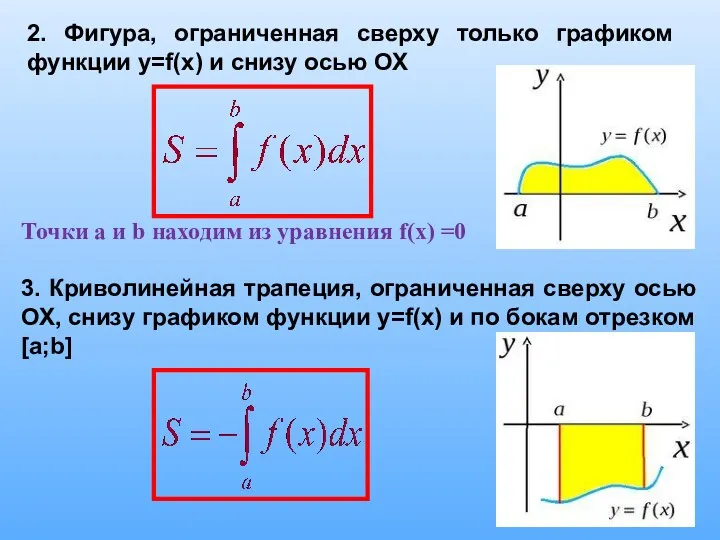
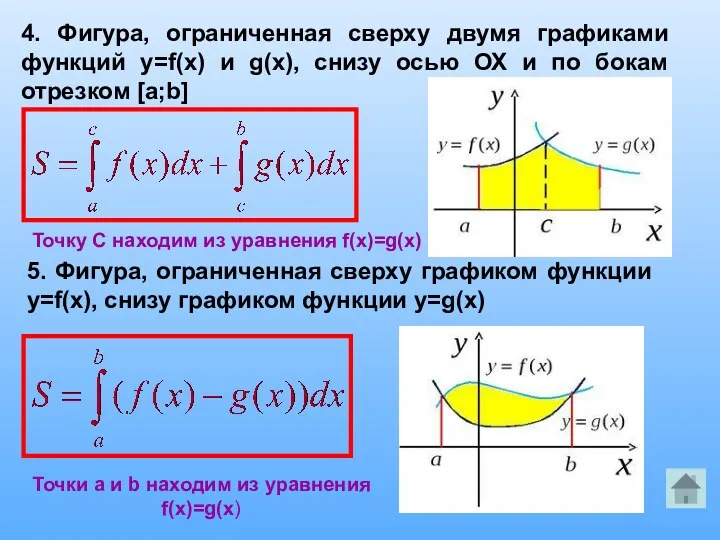
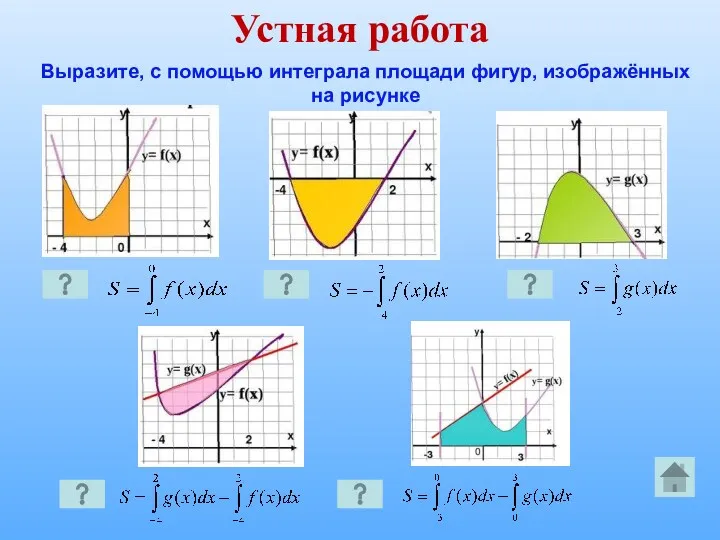
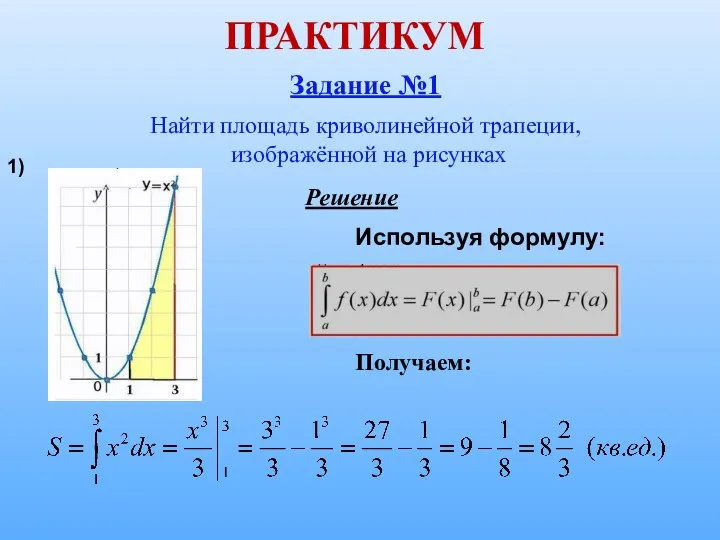
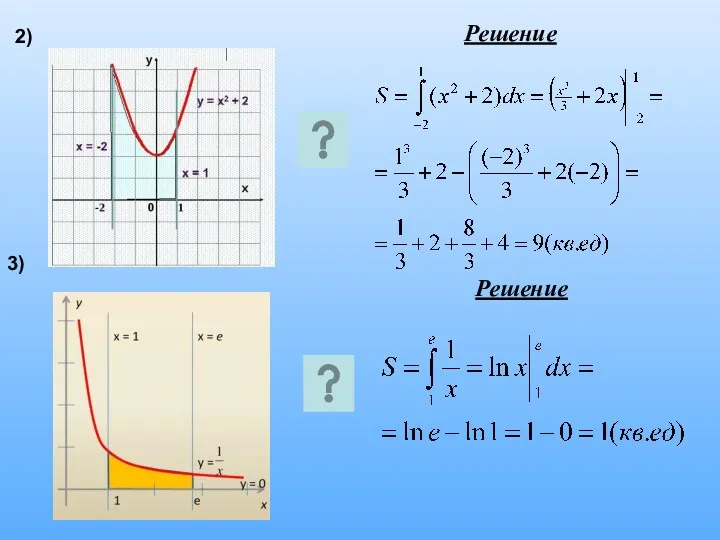
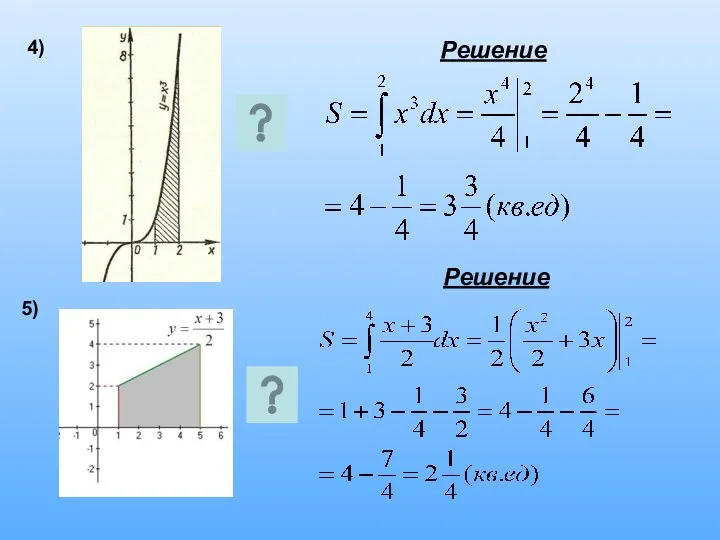
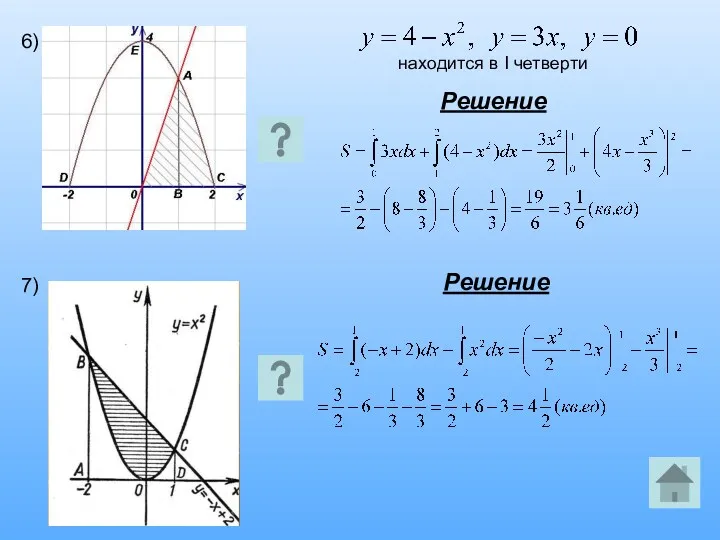
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.












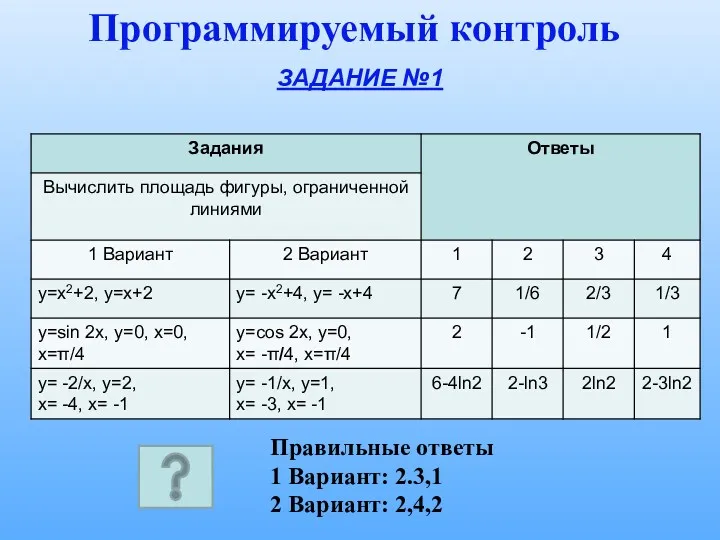





 Наибольшее и наменьшее значения функции на отрезке
Наибольшее и наменьшее значения функции на отрезке Обыкновенные дроби. Дробь как результат деления натуральных чисел
Обыкновенные дроби. Дробь как результат деления натуральных чисел Презентация по использованию счётных палочек Кюизенера.
Презентация по использованию счётных палочек Кюизенера. Нестандартные способы решения квадратных уравнений
Нестандартные способы решения квадратных уравнений Математические фокусы - мистические способности или алгоритм
Математические фокусы - мистические способности или алгоритм Тригонометрические уравнения
Тригонометрические уравнения Действия с десятичными дробями. Повторение. Первые уроки математики в 6 классе
Действия с десятичными дробями. Повторение. Первые уроки математики в 6 классе Probability Concepts
Probability Concepts Дидактическая игра для детей среднего дошкольного возраста Пятый лишний.
Дидактическая игра для детей среднего дошкольного возраста Пятый лишний. Числовые промежутки
Числовые промежутки Средняя линия (8 класс)
Средняя линия (8 класс) Вписанный в окружность треугольник
Вписанный в окружность треугольник Бағасы. Саны. Құны
Бағасы. Саны. Құны Математический бой. 6 класс
Математический бой. 6 класс Компьютерная технология. Наблюдение
Компьютерная технология. Наблюдение Построение окружности
Построение окружности Своя игра. Математический турнир
Своя игра. Математический турнир Утворення і запис трицифрових чисел
Утворення і запис трицифрових чисел Елементи комбінаторики. Комбінаторні правила суми та добутку
Елементи комбінаторики. Комбінаторні правила суми та добутку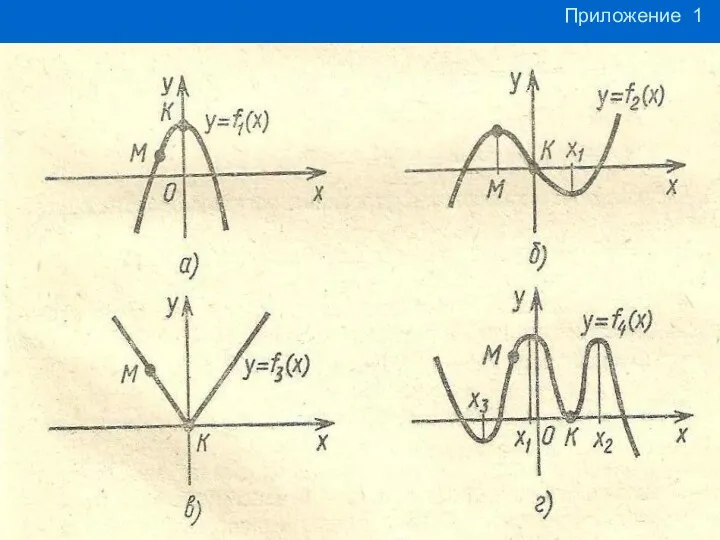 Графики функций
Графики функций Внеклассное Математическое ассорти. 6 класс
Внеклассное Математическое ассорти. 6 класс Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений Перестановки
Перестановки Математика. 1 класс. Урок 49. Число ноль. Цифра 0 - Презентация
Математика. 1 класс. Урок 49. Число ноль. Цифра 0 - Презентация Построение сечений многогранников
Построение сечений многогранников решение неравенств второй степени с помощью графика квадратичной функции
решение неравенств второй степени с помощью графика квадратичной функции Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої
Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої