Слайд 2

Тема 4: Симплекс-метод розв'язання задач лінійної оптимізації
План
Канонічна форма загальної задачі
ЛО.
Правила переходу від загальної задачі лінійної оптимізації до канонічної.
Приклад зведення задачі ЛО до канонічної форми.
Основні властивості розв'язків задач ЛО.
Симплекс-метод розв'язання задач ЛО.
Алгоритм симплекс-методу розв'язання задач ЛО.
Правила перебудови симплекс-таблиці за методом Жордана-Гаусса.
Правило прямокутника перебудови симплексної таблиці.
Варіанти розв'язку задачі ЛО симплекс-методом.
Приклад розв'язання задачі ЛО симплекс-методом.
Слайд 3

Канонічна форма загальної задачі
лінійної оптимізації
Слайд 4

Правила переходу від загальної задачі лінійної оптимізації до канонічної
Цільову функцію необхідно
максимізувати.
В системі обмежень всі праві частини невід’ємні.
Всі обмеження в системі є рівняннями (явні).
Всі змінні мають невід’ємний характер.
Слайд 5

Правила переходу від загальної задачі лінійної оптимізації до канонічної
Залишкова змінна. Нерівності
типу “≤” зазвичай можна інтерпретувати як обмеження на використання деяких ресурсів. В нерівність вона входить зі знаком “+”.
Надлишкова змінна. Нерівність типу “≥” показує на те, що “щось” повинно бути не менш за деяку величину. В нерівність вона входить зі знаком “–”.
Слайд 6

Правила переходу від загальної задачі лінійної оптимізації до канонічної
Слайд 7

Приклад зведення задачі ЛО до канонічної форми
Слайд 8

Приклад зведення задачі ЛО до канонічної форми
Канонічна форма задачі (4)-(6):
Слайд 9

Основні властивості розв’язків
задач лінійної оптимізації
Теорема 1. Множина всіх планів
задачі лінійної оптимізації опукла.
Теорема 2. Якщо задача лінійної оптимізації має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
Слайд 10

Основні властивості розв’язків
задач лінійної оптимізації
Слайд 11

Основні властивості розв’язків
задач лінійної оптимізації
Слайд 12

Основні властивості розв’язків
задач лінійної оптимізації
Слайд 13

Симплекс-метод розв'язання
задач лінійної оптимізації
Симплекс-метод – це поетапна обчислювальна процедура,
в основу якої покладено принцип послідовного покращення значень цільової функції переходом від одного опорного плану задачі лінійної оптимізації до іншого.
Алгоритм симплекс-методу завжди починається з деякого опорного розв’язку (плану) і потім намагається знайти інший опорний план, який покращує значення цільової функції.
Слайд 14

Алгоритм симплекс-методу розв'язання задач ЛО
Визначення початкового опорного плану задачі ЛО.
Побудова
симплексної таблиці.
Перевірка опорного плану на оптимальність за допомогою оцінок. Якщо план не оптимальний, то переходять до нового опорного плану або встановлюють, що оптимального плану не існує.
Перехід до нового опорного плану задачі, тобто розрахунок нової симплексної таблиці.
Повторення дій, починаючи з п. 3.
Слайд 15

Алгоритм симплекс-методу розв'язання задач ЛО
На етапі визначення початкового опорного плану
задачі ЛО, після її зведення до канонічної форми, шукаємо m одиничних лінійно незалежних векторів, які становлять базис m-вимірного простору. Можливі такі випадки:
є необхідна кількість одиничних векторів, тоді початковий опорний план визначається безпосередньо без додаткових дій;
у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису.
Слайд 16

Алгоритм симплекс-методу розв'язання задач ЛО
Визначені одиничні лінійно незалежні вектори утворюють
базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними.
Слайд 17

Алгоритм симплекс-методу розв'язання задач ЛО
Слайд 18

Алгоритм симплекс-методу розв'язання задач ЛО
Слайд 19

Алгоритм симплекс-методу розв'язання задач ЛО
Слайд 20

Алгоритм симплекс-методу розв'язання задач ЛО
Слайд 21

Правила перебудови симплекс-
таблиці за методом Жордана-Гаусса
1. Розв’язувальний (напрямний) рядок необхідно
поділити на розв’язувальний елемент і здобуті числа записати у відповідний рядок симплексної таблиці.
2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.
3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.
4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.
5. Усі інші елементи наступної симплекс-таблиці розраховують за правилом прямокутника.
Слайд 22

Правило прямокутника перебудови симплекс-таблиці
Слайд 23

Варіанти розв'язку задачі ЛО симплекс-методом
Слайд 24

Варіанти розв'язку задачі ЛО симплекс-методом
Слайд 25

Приклад розв'язання задачі ЛО симплекс-методом
Слайд 26

Приклад розв'язання задачі ЛО симплекс-методом
Слайд 27
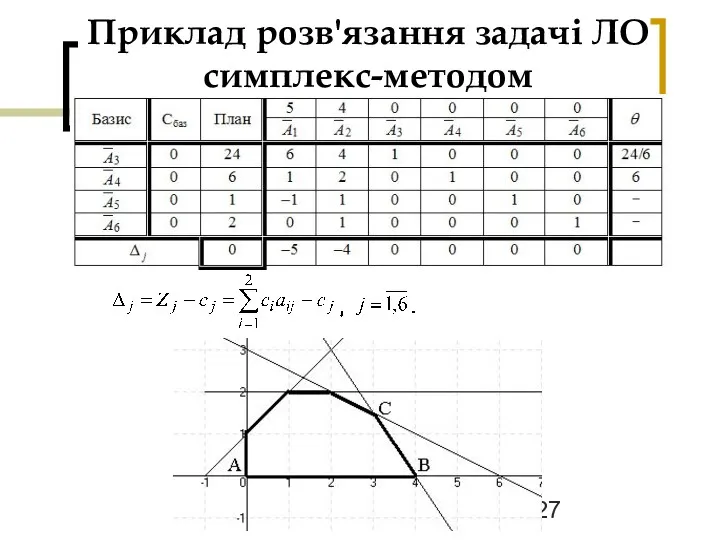
Приклад розв'язання задачі ЛО симплекс-методом
Слайд 28
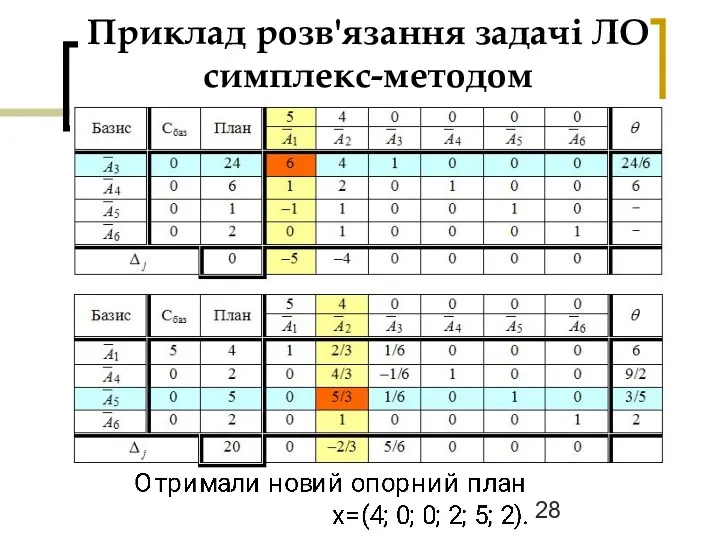
Приклад розв'язання задачі ЛО симплекс-методом
Слайд 29
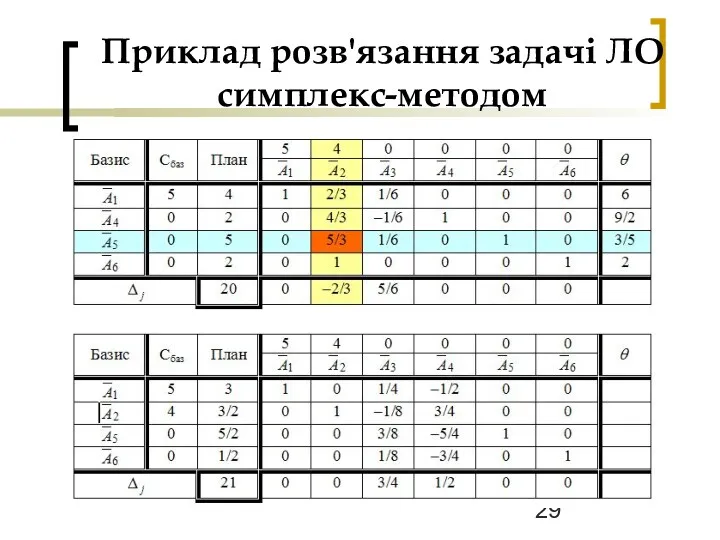
Приклад розв'язання задачі ЛО симплекс-методом
Слайд 30

Приклад розв'язання задачі ЛО симплекс-методом





























 Развитие теории вероятностей. Основные элементы комбинаторики
Развитие теории вероятностей. Основные элементы комбинаторики Осевая симметрия. Геометрия
Осевая симметрия. Геометрия Построение сечений многогранника
Построение сечений многогранника Среднее арифметическое
Среднее арифметическое Презентация урока-сказки на тему Решение задач
Презентация урока-сказки на тему Решение задач Увлекательная математика. Сложение и вычитание
Увлекательная математика. Сложение и вычитание Тени в ортогональных проекциях
Тени в ортогональных проекциях Линейная модель парной регрессии. Метод наименьших квадратов
Линейная модель парной регрессии. Метод наименьших квадратов Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости Аналитические функции и конформные отображения
Аналитические функции и конформные отображения Случаи деления, когда делимое меньше делителя
Случаи деления, когда делимое меньше делителя Закрепление знаний по математике 3 класс 1 четверть
Закрепление знаний по математике 3 класс 1 четверть Линейная функция и ее свойства
Линейная функция и ее свойства Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости Тест по математике 4 класс Диск
Тест по математике 4 класс Диск Применение распределительного свойства умножения. 6 класс
Применение распределительного свойства умножения. 6 класс Преобразование симметрии в пространстве. Симметрия в природе и на практике
Преобразование симметрии в пространстве. Симметрия в природе и на практике Формулы сокращенного умножения
Формулы сокращенного умножения Развитие самоконтроля на уроках математики
Развитие самоконтроля на уроках математики Средняя линия
Средняя линия Деление с остатком
Деление с остатком Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Деление натуральных чисел
Деление натуральных чисел Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Ломаная. Многоугольники
Ломаная. Многоугольники Применение методов статистического анализа
Применение методов статистического анализа Транспортная задача линейного программирования
Транспортная задача линейного программирования Математикалық статистика негіздері
Математикалық статистика негіздері