Основы аналитической геометрии презентация

1. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ

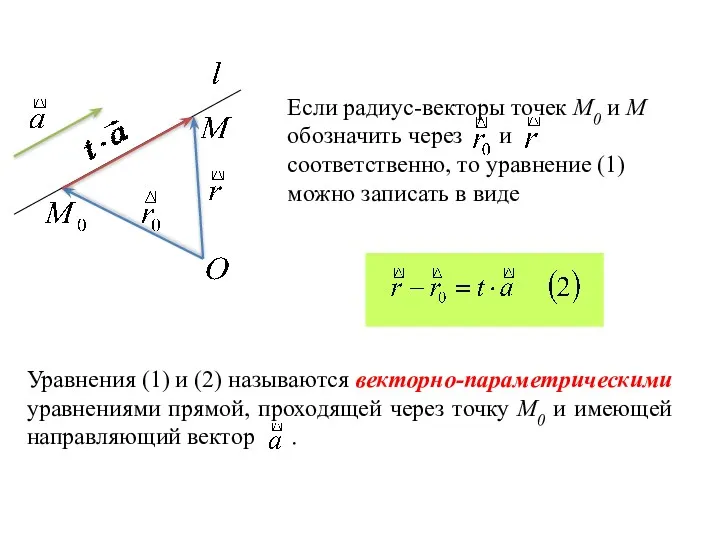
Если радиус-векторы точек М0 и М обозначить через и соответственно, то уравнение (1) можно записать в виде
Уравнения (1) и (2) называются векторно-параметрическими уравнениями прямой, проходящей через точку М0 и имеющей направляющий вектор .

В координатной записи уравнение (1) имеет вид:
или
Система уравнений (3) называется параметрическим уравнением прямой, проходящей через точку М0(x0, y0) и имеющей направляющий вектор .

Параметрическое уравнение (3) равносильно уравнению, которое называется каноническим уравнением прямой на плоскости.
Замечание: в каноническом уравнении (4) допускаются значения а1 = 0 или а2=0. это не означает, что можно выполнить деление на 0. Из канонического уравнения получаем информацию о том, что направляющий вектор прямой имеет координаты, из которых одна нулевая. Причем в случает а1 = 0 уравнение прямой имеет вид x - x0 = 0 или x = x0, а в случае а2 = 0 уравнение прямой имеет вид y - y0 = 0 или y = y0.
y
x
O
y0
y = y0

Задача. Написать уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1) .
Решение: вектор
является направляющим вектором прямой. Значит, прямая, проходящая через заданные две точки М0(x0, y0) и М1(x1, y1) - это та же прямая, которая проходит через точку М0(x0, y0) и имеет направляющий вектор .
Уравнение этой прямой по формуле (4) имеет вид:
Уравнение (5) и есть уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1).
М0(x0, y0)
М1(x1, y1)

Теорема. Всякая прямая на плоскости задается некоторым уравнение первого порядка от двух переменных x и y
и, наоборот, любое такое уравнение является уравнением некоторой прямой на плоскости.
Уравнение (6) называется общим уравнением прямой на плоскости.
Замечание: Вектор является направляющим вектором прямой, заданной общим уравнением.

Замечание.
Пусть в общем уравнении прямой (6) коэффициент В≠0. Тогда уравнение (6) можно представить в виде
или
Где
Число k называется угловым коэффициентом прямой, а уравнение (7) – уравнением прямой с угловым коэффициентом.
Т.о. любая прямая, не параллельная оси Оy (В≠0), может быть задана уравнением с угловым коэффициентом.

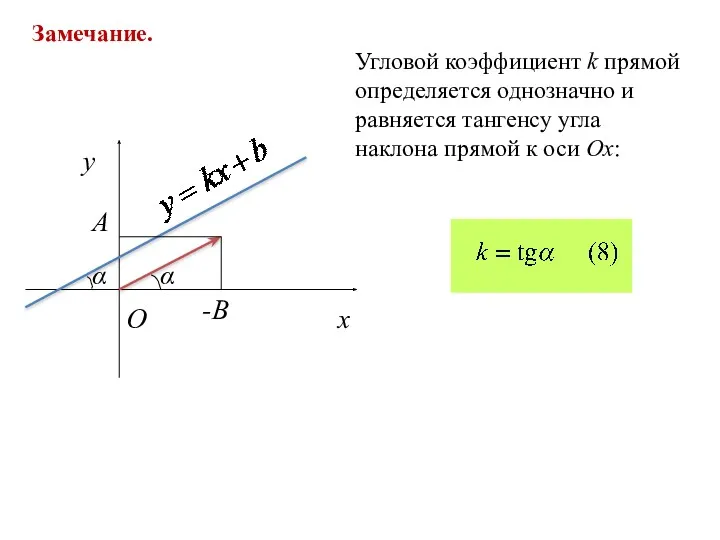
Замечание.
Угловой коэффициент k прямой определяется однозначно и равняется тангенсу угла наклона прямой к оси Ox:

2. НОРМАЛЬНЫЙ ВЕКТОР ПРЯМОЙ. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ

Опр. Если вектор перпендикулярен направляющему вектору прямой l, то он называется нормальным вектором прямой l.
y
x
O
l

Теорема. Пусть прямая задана общим уравнением:
Тогда вектор является нормальным вектором этой прямой.

Задача. Найти уравнение прямой l, которая проходит через точку М0(x0, y0) и имеет нормальный вектор .
Решение:
Возьмем на прямой l произвольную точку М(x, y) и рассмотрим вектор .
Т.к. векторы перпендикулярны,
то их скалярное произведение равно нулю:
, т.е.
Уравнение (8) называется уравнением прямой, проходящей через точку М0(x0, y0) перпендикулярно вектору .
y
x
O
М0(x0, y0)
М(x, y)

Теорема. Расстояние d от точки М0(x0, y0) до прямой, заданной общим уравнением
вычисляется формулой

Задача. Найти расстояние от точки М0(1, 5) до прямой, заданной общим уравнением 3x – 4y – 3 = 0.
Решение:
По формуле (9) имеем

3. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ. УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПРЯМЫХ

Пусть l1 и l2 – две произвольные прямые на плоскости.
Опр. Углом между двумя прямыми l1 и l2 на плоскости называется угол между их направляющими векторами.

Пусть l1 и l2 заданы общими уравнениями:
- направляющие векторы.
Тогда косинус угла между прямыми вычисляется по формуле:

условие параллельности прямых: прямые l1 и l2 параллельны, если их направляющие векторы
коллинеарны, т.е. координаты этих векторов пропорциональны
условие перпендикулярности прямых: прямые l1 и l2 перпендикулярны, если нормальные векторы
ортогональны, т.е.