Содержание
- 2. Литература Лобоцкая Н.Л. Основы высшей математики 2015, Москва Ремизов А.Н. Максина А.Г., Потапенко А.Я. Медицинская и
- 3. Определение производной Если существует предел отношения то функция f(x) называется дифференцируемой в точке х, а значение
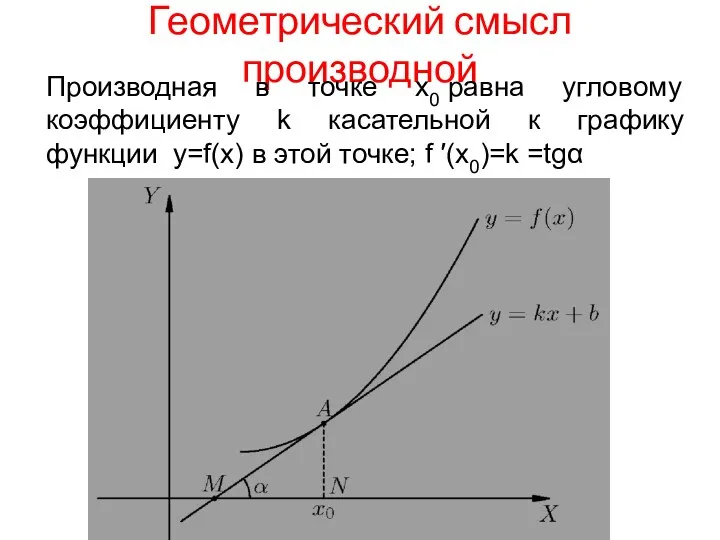
- 4. Геометрический смысл производной Производная в точке x0 равна угловому коэффициенту k касательной к графику функции y=f(x)
- 5. Правила дифференцирования
- 6. Производные элементарных функций
- 7. Пример. Найти производную функции . Сначала преобразуем данную функцию: Производная сложной функции Если y=f(g(x)), то где
- 8. Дифференциал функции Дифференциалом df(x) функции f(x) в точке х называется произведение производной от функции f(x) в
- 9. Связь между дифференциалом функции и её приращением Дифференциал функции, в общем случае отличаясь от приращения функции,
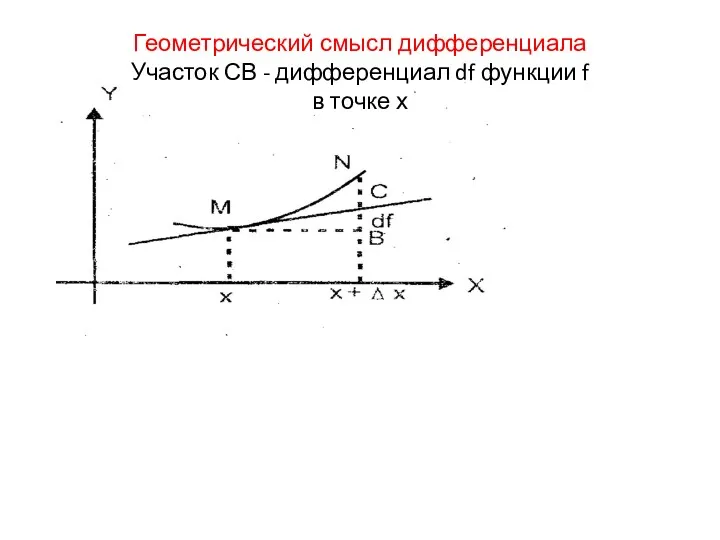
- 10. Геометрический смысл дифференциала Участок СВ - дифференциал df функции f в точке х
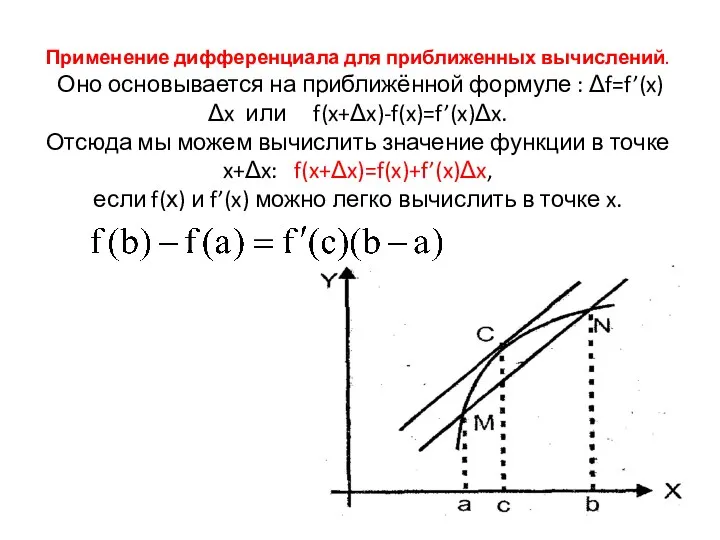
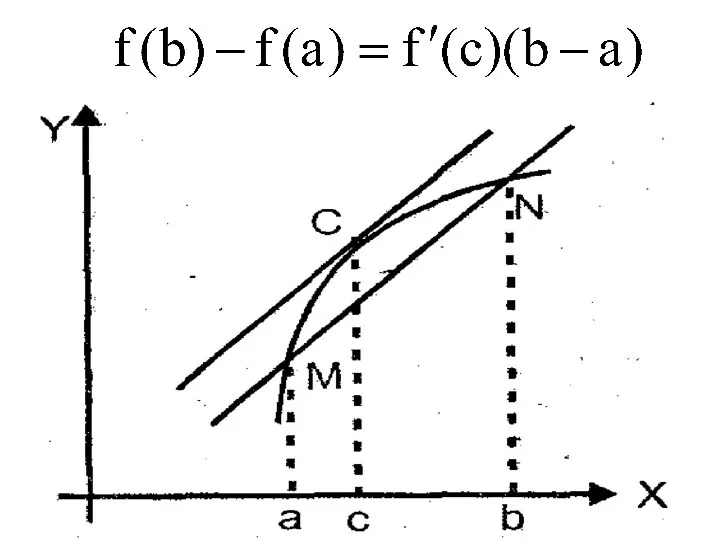
- 11. Применение дифференциала для приближенных вычислений. Оно основывается на приближённой формуле : Δf=f’(x)Δx или f(x+Δx)-f(x)=f’(x)Δx. Отсюда мы
- 13. Применение производной при исследовании функции Теорема о признаке возрастания и убывания функции. Если производная функции положительна
- 14. Порядок действий при исследовании функции. 1. Найти область определения функции. 2.Найти производную функции и определить точки,
- 15. Корни этого уравнения являются экстремумами функции. 4. Найти критические точки функции, как совокупность всех экстремумов и
- 16. 6.По знаку производной найти интервалы возрастания и убывания функции. 7. Найти точки экстремумов функции.
- 17. Первообразная функция Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой
- 19. Свойства интегралов: где u, v, w – некоторые функции от х.
- 20. Методы интегрирования А) Непосредственное интегрирование. Б) Способ подстановки (замены переменных). Сделаем замену В) Интегрирование по частям
- 21. Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)
- 22. Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x)
- 23. Определение: Если при любых разбиениях отрезка [a, b] таких, что maxΔxi→ 0 и произвольном выборе точек
- 27. Дифференциальное уравнение первого порядка имеет вид F(x , y, y′) = 0 . Если это уравнение
- 28. Делением обеих частей уравнения на произведение Q1 (y)P2 (x ) может быть приведено к уравнению с
- 30. Скачать презентацию












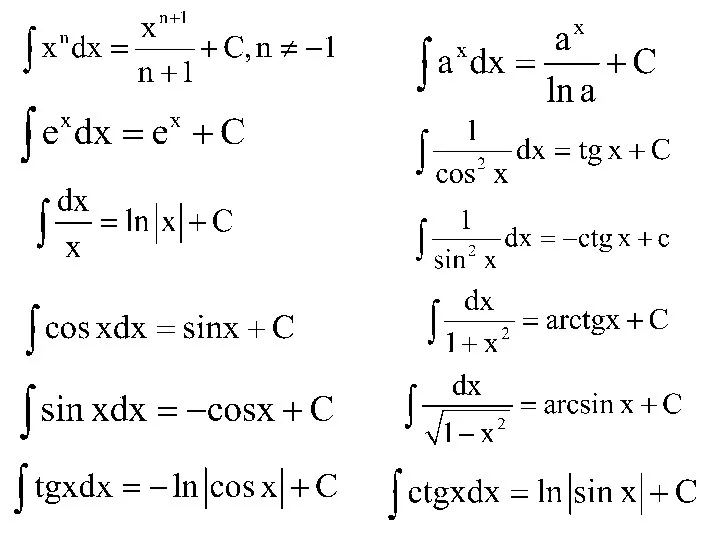


![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/335028/slide-20.jpg)

![Определение: Если при любых разбиениях отрезка [a, b] таких, что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/335028/slide-22.jpg)





 Взаимно-простые числа
Взаимно-простые числа Неравенства и системы неравенств с двумя переменными
Неравенства и системы неравенств с двумя переменными Случайные величины
Случайные величины Математика 3 класс Тема: Решение задач и уравнений
Математика 3 класс Тема: Решение задач и уравнений Порядок выполнения действий в выражении.
Порядок выполнения действий в выражении. 1-2 класс. Интерактивная игра-тренажёр Зимняя сказка (сложение в пределах 20)
1-2 класс. Интерактивная игра-тренажёр Зимняя сказка (сложение в пределах 20) Уравнения с модулем. Устная работа, самостоятельная работа
Уравнения с модулем. Устная работа, самостоятельная работа Предельные теоремы теории вероятностей и закон больших чисел
Предельные теоремы теории вероятностей и закон больших чисел Элементы алгебры логики. Математические основы информатики. Таблицы истинности
Элементы алгебры логики. Математические основы информатики. Таблицы истинности Прямоугольный параллелепипед
Прямоугольный параллелепипед Розв'язування компетентнісних задач. 9 класс
Розв'язування компетентнісних задач. 9 класс Решение неравенств второй степени. 9 класс
Решение неравенств второй степени. 9 класс Построение сечений многогранников на основе аксиоматики
Построение сечений многогранников на основе аксиоматики Системы линейных уравнений
Системы линейных уравнений Интерактивный плакат Геометрические фигуры. 1-4 класс
Интерактивный плакат Геометрические фигуры. 1-4 класс Корреляционный анализ
Корреляционный анализ Координатная плоскость
Координатная плоскость Путешествие в страну математики
Путешествие в страну математики Линейная и квадратичная функции и их графики
Линейная и квадратичная функции и их графики Квадратные уравнения и способы их решения
Квадратные уравнения и способы их решения Понятие дроби. Основные свойства дроби
Понятие дроби. Основные свойства дроби Дидактические игры на уроках математики
Дидактические игры на уроках математики Дифференциальные уравнения
Дифференциальные уравнения Наибольшее и наименьшее значение функции на отрезке
Наибольшее и наименьшее значение функции на отрезке Теорема Пифагора. Египетский треугольник
Теорема Пифагора. Египетский треугольник Делители и кратные
Делители и кратные Алгебра логики и таблицы истинности. (лекция 4)
Алгебра логики и таблицы истинности. (лекция 4) Прибавление чисел 7, 8, 9.
Прибавление чисел 7, 8, 9.