Содержание
- 2. 2.1. ЗАДАНИЕ ОТНОШЕНИЙ Элементы множества могут находиться в некоторых отношениях R между собой, с элементами других
- 3. Например, пусть x, y ∈ X и x = 2, y = 4. Если xRy, т.е.
- 4. Бинарное отношение R — это подмножество декартова произведения множеств X и Y: Пример. X = {x1,
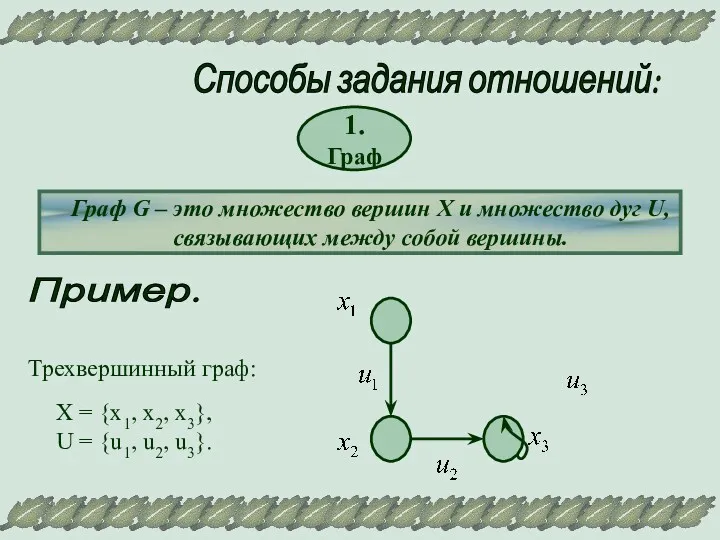
- 5. Способы задания отношений: 1. Граф Граф G – это множество вершин X и множество дуг U,
- 6. Так как каждая дуга соединяет две вершины, то U = {u1, u2, u3}= {х1х2, x2x3, x3x3}.
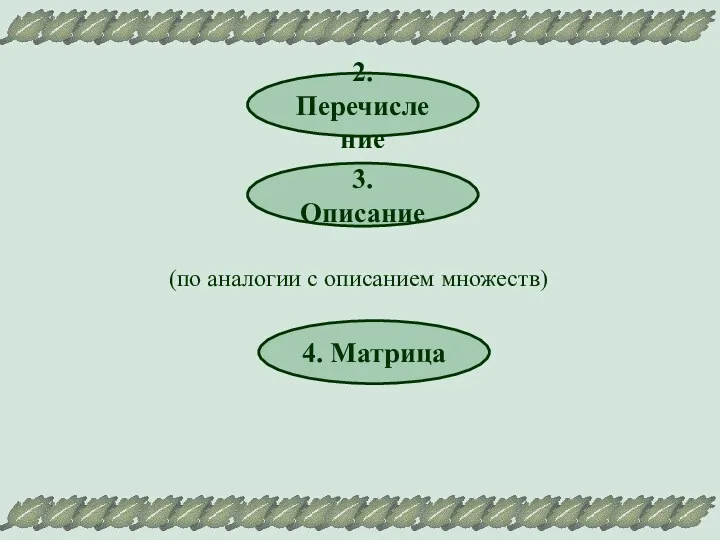
- 7. 2. Перечисление 3. Описание (по аналогии с описанием множеств) 4. Матрица
- 8. Матрица бинарного отношения R на множестве X |X| = n – это квадратная матрица C порядка
- 9. Пример 1. Дано множество X = {1, 2, 3, 4, 5, 6}, на котором задано отношение
- 11. Скачать презентацию






 Тест по теме: Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости
Тест по теме: Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости Деление с остатком методом подбора
Деление с остатком методом подбора Median, bisector and the height of the triangle
Median, bisector and the height of the triangle Начертательная геометрия. Прямая линия
Начертательная геометрия. Прямая линия Делимость чисел в жизни человека
Делимость чисел в жизни человека postroenie_paraboly_0
postroenie_paraboly_0 Степень с натуральным показателем
Степень с натуральным показателем Логарифмы и их применение
Логарифмы и их применение Числовая последовательность, виды последовательностей и способы их задания
Числовая последовательность, виды последовательностей и способы их задания Урок математики. 2 класс. Час. Минута.
Урок математики. 2 класс. Час. Минута. Применение активных методов и форм обучения на уроках математики
Применение активных методов и форм обучения на уроках математики Статистические характеристики
Статистические характеристики Презентация по использованию сказочного и универсального дидактического материала цветных счетных палочек Кюизенера в обучении математике
Презентация по использованию сказочного и универсального дидактического материала цветных счетных палочек Кюизенера в обучении математике Конические сечения
Конические сечения Великие геометры России
Великие геометры России Тренажёр по математике
Тренажёр по математике Методическая разработка урока-путешествия по теме:Деление на двузначное и трёхзначное число
Методическая разработка урока-путешествия по теме:Деление на двузначное и трёхзначное число Усеченный конус
Усеченный конус Математичні хвилинки
Математичні хвилинки Тела и поверхности вращения. Цилиндр
Тела и поверхности вращения. Цилиндр Тренажёр Увеличить, уменьшить число на 1
Тренажёр Увеличить, уменьшить число на 1 Matematik modellashtirish, sonli tahlil usullarini tizimlarda amalga oshirish. Hisobli eksperiment
Matematik modellashtirish, sonli tahlil usullarini tizimlarda amalga oshirish. Hisobli eksperiment Компьютерная технология. Наблюдение
Компьютерная технология. Наблюдение Тест по теме: Векторы в пространстве
Тест по теме: Векторы в пространстве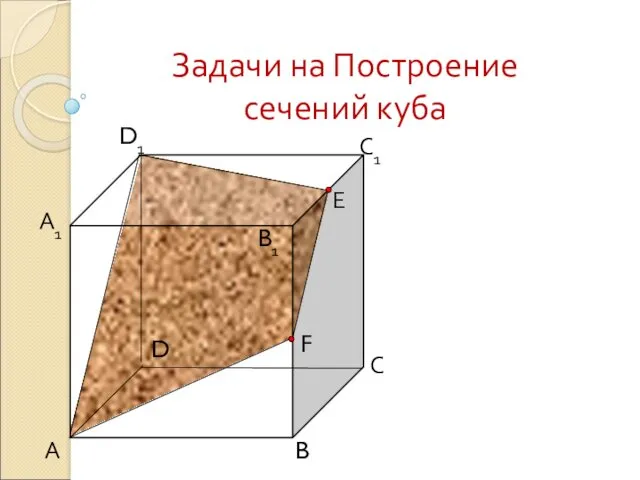 Задачи на Построение сечений куба
Задачи на Построение сечений куба Урок-путешествие к острову Натуральных чисел
Урок-путешествие к острову Натуральных чисел Свойство медианы равнобедренного треугольника
Свойство медианы равнобедренного треугольника Признаки делимости на 3 и 9
Признаки делимости на 3 и 9